
第26卷第10期 半导体学报 Vol.26 No.10 2005年10月 CHINESE JOURNAL OF SEMICONDUCTORS Oct.,2005 一种采用开关阶跃电容的压控振荡器(上): 调谐特性的理论分析* 唐长文何捷闵昊 (复旦大学专用集成电路与系统国家重点实验室,上海200433) 摘要:针对采用阶跃可变电容的电感电容压控振荡器电路,本文提出了一种振荡器调谐特性的时域分析方法—— 周期计算技术,通过对电感电容谐振回路中电感的上V曲线分析,详细地阐述了阶跃可变电容能够实现线性压控 的物理机理和本质.对差分调谐电感电容压控振荡器的调谐特性也进行了详细的分析.SPICE电路仿真验证了调 谐特性理论分析的正确性. 关键词:阶跃可变电容;MO管可变电容;开关阶跃电容;电感电容压控振荡器;振荡调谐曲线;周期计算技术 EEACC:1230B 中图分类号:TN4 文献标识码:A 文章编号:0253-4177(2005)10-2010-12 电容都采用pn结12,1.随着对MOS管电容的cv 1简介 曲线特性的不断认识,发现振荡器的实际等效电容 是振荡电压波形对MOS管电容的CV曲线的一个 电感电容压控振荡器是现代射频集成电路中最 周期内的平均值16~101.因此,阶跃M0S管可变电容 重要的模块之一随着片上电感和片上可变电容实 也能够实现振荡器的调谐特性,这样MOS管可变 现问题的逐渐明朗,近十年来出现了大量关于电感 电容慢慢被学术界和工艺界所接受.由于累积型 电容压控振荡器设计的文献1~41,[6~151.片上可变电 MOS管的CV曲线比反型MOS管要缓一些,人们 容的实现方式主要有三种:pn结,反型MOS管电 就普遍认为缓变的累积型MOS管电容比陡变反型 容,累积型MOS管电容.pn结可变电容是反偏结电 MOS管电容性能更好,能够得到更加线性的频率- 容在反偏电压的控制下实现压控电容特性的.而 电压调谐曲线.然而这种观点是不正确的,通过本 MOS管电容的C-V特性却截然不同,呈现出阶跃 文采用阶跃可变电容的电感电容压控振荡器的调谐 特性4,5.MOS管电容根据其压控电压的不同而工 特性分析,发现陡变反型MOS管电容也能够实现 作在两个不同的区域,反型MOS管电容只工作在 高线性的调谐特性12~14 反型和耗尽两个区域,而累积型MOS管只工作在 目前大多数关于压控振荡器的文献~都是压 累积和耗尽两个区.在反型区或累积区的MOS管 控振荡器相位噪声、功耗和调谐范围等方面的优化 电容有最大电容值Cox=/ax;在耗尽区的电容为最 研究,而对于压控振荡器的调谐曲线特性研究的文 小电容值,栅氧化电容Cx与耗尽层电容C的串联. 献相对比较少.虽然电感电容压控振荡器的实现是 压控电压在MOS管的阈值电压Vh附近时,电容在 一件很容易的事情,但是压控振荡器电路中的许多 最大值与最小值之间过渡.因此与pn结电容不同 简单问题并没有得到完全的解决.譬如,阶跃可变电 的是,MOS管的CV曲线的压控范围比较小.正因 容是如何实现对振荡器频率进行控制的?压控振荡 为这种原因,早期出现在压控振荡器中的片上可变 器的调谐特性的内在物理本质是什么?采用阶跃可 ·上海市科学技术委员会(批准号:037062019)和上海市应用材料研究与发展基金(批准号:0425)资助项目 唐长文男,1977年出生,助理研究员,主要研究方向为低相位噪声电感电容压控振荡器和CM0S射频电视调谐器. 何捷男,1978年出生,博士研究生,主要研究方向为全集成射频频率综合器设计. 2005-01-10收到,2005-06-15定稿 c2005中国电子学会
第 26 卷 第 10 期 2005 年 10 月 半 导 体 学 报 CHINESE JOURNAL OF SEMICONDUCTORS Vol. 26 No. 10 Oct. ,2005 3 上海市科学技术委员会(批准号 :037062019) 和上海市应用材料研究与发展基金(批准号 :0425) 资助项目 唐长文 男 ,1977 年出生 ,助理研究员 ,主要研究方向为低相位噪声电感电容压控振荡器和 CMOS 射频电视调谐器. 何 捷 男 ,1978 年出生 ,博士研究生 ,主要研究方向为全集成射频频率综合器设计. 2005201210 收到 ,2005206215 定稿 ν 2005 中国电子学会 一种采用开关阶跃电容的压控振荡器(上) : 调谐特性的理论分析3 唐长文 何 捷 闵 昊 (复旦大学专用集成电路与系统国家重点实验室 , 上海 200433) 摘要 : 针对采用阶跃可变电容的电感电容压控振荡器电路 ,本文提出了一种振荡器调谐特性的时域分析方法 ——— 周期计算技术. 通过对电感电容谐振回路中电感的 I2V 曲线分析 ,详细地阐述了阶跃可变电容能够实现线性压控 的物理机理和本质. 对差分调谐电感电容压控振荡器的调谐特性也进行了详细的分析. SPICE 电路仿真验证了调 谐特性理论分析的正确性. 关键词 : 阶跃可变电容 ; MOS管可变电容; 开关阶跃电容; 电感电容压控振荡器 ; 振荡调谐曲线 ; 周期计算技术 EEACC : 1230B 中图分类号 : TN4 文献标识码 : A 文章编号 : 025324177 (2005) 1022010212 1 简介 电感电容压控振荡器是现代射频集成电路中最 重要的模块之一. 随着片上电感和片上可变电容实 现问题的逐渐明朗 ,近十年来出现了大量关于电感 电容压控振荡器设计的文献[1~4 ] ,[ 6~15 ] . 片上可变电 容的实现方式主要有三种 :p n 结 ,反型 MOS 管电 容 ,累积型 MOS 管电容. p n 结可变电容是反偏结电 容在反偏电压的控制下实现压控电容特性的. 而 MOS 管电容的 C2V 特性却截然不同 ,呈现出阶跃 特性[ 4 ,5 ] . MOS 管电容根据其压控电压的不同而工 作在两个不同的区域 ,反型 MOS 管电容只工作在 反型和耗尽两个区域 ,而累积型 MOS 管只工作在 累积和耗尽两个区. 在反型区或累积区的 MOS 管 电容有最大电容值 Cox =ε/ tox ;在耗尽区的电容为最 小电容值 ,栅氧化电容 Cox与耗尽层电容 Cd 的串联. 压控电压在 MOS 管的阈值电压 V th附近时 ,电容在 最大值与最小值之间过渡. 因此与 p n 结电容不同 的是 ,MOS 管的 C2V 曲线的压控范围比较小. 正因 为这种原因 ,早期出现在压控振荡器中的片上可变 电容都采用 p n 结[1 ,2 ,7 ] . 随着对 MOS 管电容的 C2V 曲线特性的不断认识 ,发现振荡器的实际等效电容 是振荡电压波形对 MOS 管电容的 C2V 曲线的一个 周期内的平均值[6~10 ] . 因此 ,阶跃 MOS 管可变电容 也能够实现振荡器的调谐特性 ,这样 MOS 管可变 电容慢慢被学术界和工艺界所接受. 由于累积型 MOS 管的 C2V 曲线比反型 MOS 管要缓一些 ,人们 就普遍认为缓变的累积型 MOS 管电容比陡变反型 MOS 管电容性能更好 ,能够得到更加线性的频率2 电压调谐曲线[5 ] . 然而这种观点是不正确的 ,通过本 文采用阶跃可变电容的电感电容压控振荡器的调谐 特性分析 ,发现陡变反型 MOS 管电容也能够实现 高线性的调谐特性[ 12~14 ] . 目前大多数关于压控振荡器的文献[1~4 ]都是压 控振荡器相位噪声、功耗和调谐范围等方面的优化 研究 ,而对于压控振荡器的调谐曲线特性研究的文 献相对比较少. 虽然电感电容压控振荡器的实现是 一件很容易的事情 ,但是压控振荡器电路中的许多 简单问题并没有得到完全的解决. 譬如 ,阶跃可变电 容是如何实现对振荡器频率进行控制的 ? 压控振荡 器的调谐特性的内在物理本质是什么 ? 采用阶跃可

第10期 唐长文等:一种采用开关阶跃电容的压控振荡器(上):调谐特性的理论分析 2011 变电容的压控振荡器的调谐特性分析就是本文需要 研究的重点 Mp 虽然近几年有文献[61对压控振荡器调谐特 性问题进行了详细探讨,但是他们的方法主要是通 000 0000 过谐波平衡近似分析求得基波频率上的等效电容, 由于谐波近似方法忽略了高次谐波分量对等效电容 的影响,因此在一定程度上会引入精度误差.文献 [8]提出了一种频率-电压调谐曲线分析方法,并且 采用数值计算的方法得到了子V调谐曲线.数值计 算是一个复杂而且费时的方法,特别是在改变偏置 Mn3 C(n 电流的情况下,整个数值计算方法需要重新进行.文 (a) g 献[7]和[10]也分析了可变电容的大信号现象,但他 们的分析只是定性地解释了大信号对有效电容和 图1CMOS互补交叉耦合型负阻结构压控振荡器(a)压控 振荡器电路图;(b)半电路等效电感电容串联回路:(c)阶跃可 子V曲线的影响.文献[9]通过可变电容小信号模型 变电容CV曲线 和非线性分析,得到了一个精简的有效电容的计算 Fig.1 CMOS complementary cross-coupled negative- 公式,从而计算出V调谐曲线.然而该方法是基 impedance LC VCO (a)LC-tank VCO;(b)Simplified 于电容的小信号模型且忽略了高次谐波分量得到 half circuit;(c)Step GV curve 的.由于阶跃可变电容的强烈非线性特性,电感电容 谐振电路的谐振波形不可能是一个理想的正弦波, y≥Vos V<Vos 1) 因此该有效电容的计算公式并不能够真正描述电感 Cmin, 电容谐振电路中的实际有效电容特性2,) 其中y为阶跃可变电容cV曲线偏移电压.有效 本文的第二部分采用周期计算技术详细分析了 控制电压为Vr=Vcrl+Vos, 单端调谐压控振荡器的振荡周期,详细阐述了阶跃 图1(b)中串联谐振电路的谐振电压波形如图2 可变电容能够对振荡器周期进行控制的内在机制; 所示,它由两个正弦波形相拼接而成,其转折点电压 第三部分进一步分析了差分调谐的阶跃可变电容是 为有效控制电压V.根据有效控制电压Vr的大小 如何实现对压控振荡器周期进行差分调谐的;第四 可以将整个压控范围划分为以下四种情况: 部分给出了SPICE仿真结果与理论分析的比较:最 (I)当Vmk·Amn,也就是有效控制电压很 后是本文的结论 低时,电感电容谐振电路的可变电容始终是最大电 容值Cx,谐振波形是一个最小幅值Amm的正弦波, 2单端调谐的压控振荡器 振荡频率为最小频率4n; (2)当Vrk+Amax,也就是有效控制电压很 互补交叉耦合型负阻结构的全差分电感电容压 高时,电感电容谐振电路的可变电容始终是最小电 控振荡器如图1(a)所示,它由交叉耦合的pMOS管 容值Cmn,谐振波形是一个最大幅值Amx的正弦波, 对和nMOS管对产生一个负跨导,抵消片上电感和 振荡频率为最大频率an; 可变电容中的串联电阻,从而使得电感电容谐振电 (3)当Vk·An<V<Vk时,在电压Vr以上 路能够持续振荡起来.两个片上电感的存在使得差 可变电容为最大电容值Cx,谐振波形是最小幅值 分振荡波形的直流分量是Vk.忽略片上电感和可 Amm的正弦波的一部分,频率为最小频率4m;在电 变电容中的串联损耗电阻,压控振荡器的半电路可 压Vr以下可变电容为最小电容值Cmm,振荡波形是 以看作为图1(b)中的串联电感电容谐振电路).大 幅值为0Amx(0为椭圆相似系数)的正弦波的一部 多数情况下,电感电容压控振荡器采用的可变电容 分,频率为最大频率4x; 是反型MOS管和累积型MOS管电容.它们的CV (4)当Vk<V雌<Ve+Amx时,在电压Vr以上 曲线都可以近似为一个阶跃函数(图1(c) 可变电容为最大电容值Cx,幅值为0Amn(0为椭圆 相似系数)的正弦波形的一部分,频率为最小频率
第 10 期 唐长文等 : 一种采用开关阶跃电容的压控振荡器(上) :调谐特性的理论分析 变电容的压控振荡器的调谐特性分析就是本文需要 研究的重点. 虽然近几年有文献[6~10 ] 对压控振荡器调谐特 性问题进行了详细探讨 ,但是他们的方法主要是通 过谐波平衡近似分析求得基波频率上的等效电容. 由于谐波近似方法忽略了高次谐波分量对等效电容 的影响 ,因此在一定程度上会引入精度误差. 文献 [8 ]提出了一种频率2电压调谐曲线分析方法 ,并且 采用数值计算的方法得到了 f2V 调谐曲线. 数值计 算是一个复杂而且费时的方法 ,特别是在改变偏置 电流的情况下 ,整个数值计算方法需要重新进行. 文 献[ 7 ]和[ 10 ]也分析了可变电容的大信号现象 ,但他 们的分析只是定性地解释了大信号对有效电容和 f2V 曲线的影响. 文献[9 ]通过可变电容小信号模型 和非线性分析 ,得到了一个精简的有效电容的计算 公式 ,从而计算出 f2V 调谐曲线. 然而该方法是基 于电容的小信号模型且忽略了高次谐波分量得到 的. 由于阶跃可变电容的强烈非线性特性 ,电感电容 谐振电路的谐振波形不可能是一个理想的正弦波 , 因此该有效电容的计算公式并不能够真正描述电感 电容谐振电路中的实际有效电容特性[12 ,13 ] . 本文的第二部分采用周期计算技术详细分析了 单端调谐压控振荡器的振荡周期 ,详细阐述了阶跃 可变电容能够对振荡器周期进行控制的内在机制 ; 第三部分进一步分析了差分调谐的阶跃可变电容是 如何实现对压控振荡器周期进行差分调谐的 ;第四 部分给出了 SPICE 仿真结果与理论分析的比较 ;最 后是本文的结论. 2 单端调谐的压控振荡器 互补交叉耦合型负阻结构的全差分电感电容压 控振荡器如图 1 (a) 所示 ,它由交叉耦合的 pMOS 管 对和 nMOS 管对产生一个负跨导 ,抵消片上电感和 可变电容中的串联电阻 ,从而使得电感电容谐振电 路能够持续振荡起来. 两个片上电感的存在使得差 分振荡波形的直流分量是 V dc . 忽略片上电感和可 变电容中的串联损耗电阻 ,压控振荡器的半电路可 以看作为图 1 (b) 中的串联电感电容谐振电路[ 7 ] . 大 多数情况下 ,电感电容压控振荡器采用的可变电容 是反型 MOS 管和累积型 MOS 管电容. 它们的 C2V 曲线都可以近似为一个阶跃函数(图 1 (c) ) . 图 1 CMOS 互补交叉耦合型负阻结构压控振荡器 (a) 压控 振荡器电路图 ; (b) 半电路等效电感电容串联回路 ; (c) 阶跃可 变电容 C2V 曲线 Fig. 1 CMOS complementary cross2coupled negative2 impedance LC VCO (a) LC2tank VCO ; (b) Simplified half circuit ; (c) Step C2V curve Css (V ) = Cmax , V ≥Vos Cmin , V < Vos (1) 其中 Vos为阶跃可变电容 C2V 曲线偏移电压. 有效 控制电压为 V eff = V ctr1 + Vos . 图 1 (b) 中串联谐振电路的谐振电压波形如图 2 所示 ,它由两个正弦波形相拼接而成 ,其转折点电压 为有效控制电压 V eff . 根据有效控制电压 V eff的大小 可以将整个压控范围划分为以下四种情况 : (1) 当 V eff ≤V dc - A min ,也就是有效控制电压很 低时 ,电感电容谐振电路的可变电容始终是最大电 容值 Cmax ,谐振波形是一个最小幅值 A min的正弦波 , 振荡频率为最小频率ωmin ; (2) 当 V eff ≥V dc + A max ,也就是有效控制电压很 高时 ,电感电容谐振电路的可变电容始终是最小电 容值 Cmin ,谐振波形是一个最大幅值 A max的正弦波 , 振荡频率为最大频率ωmin ; (3) 当 V dc - A min < V eff < V dc时 ,在电压 V eff 以上 可变电容为最大电容值 Cmax ,谐振波形是最小幅值 A min的正弦波的一部分 ,频率为最小频率ωmin ;在电 压 V eff以下可变电容为最小电容值 Cmin ,振荡波形是 幅值为θA max (θ为椭圆相似系数) 的正弦波的一部 分 ,频率为最大频率ωmax ; (4) 当 V dc < V eff < V dc + A max时 ,在电压 V eff以上 可变电容为最大电容值 Cmax ,幅值为θA min (θ为椭圆 相似系数) 的正弦波形的一部分 ,频率为最小频率 1102
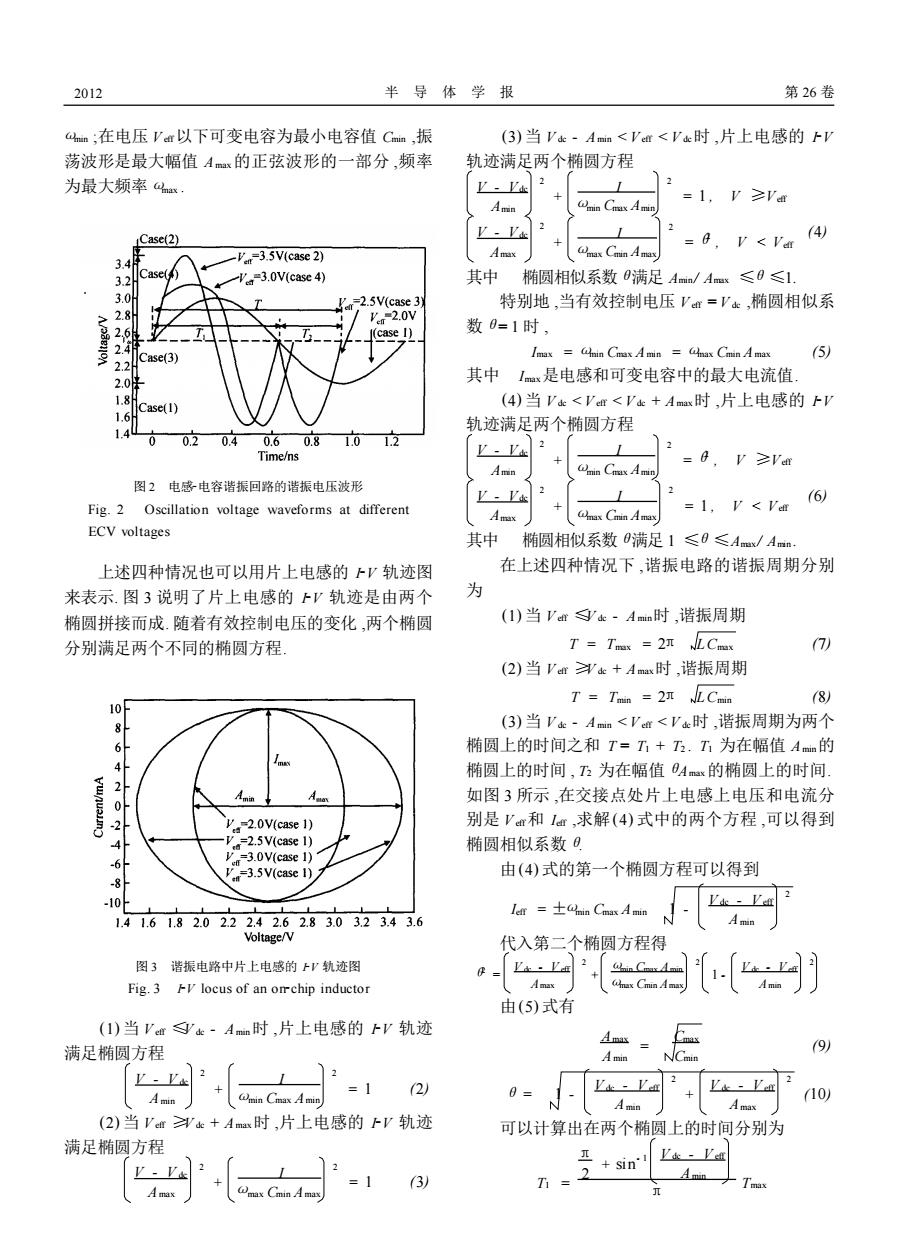
2012 半导体学报 第26卷 4m;在电压Vr以下可变电容为最小电容值Cmm,振 (3)当Vk-Amn<Ver<Vk时,片上电感的rV 荡波形是最大幅值Ax的正弦波形的一部分,频率 轨迹满足两个椭圆方程 为最大频率ax VVa =1,V≥Va Amin @min Cmax Ami V-Vae 2 L Case(2) (4 -'t-3.5V(case2) Amax cmax Cmin A mas =6.V<Va 3.4 Case( 3.2 V=3.0V(case 4) 其中椭圆相似系数0满足Amm/Am≤0≤1, 3.0H V=2.5V(case 3 特别地,当有效控制电压V=Vk,椭圆相似系 2.8 '.2.0V 26 (case I) 数0=1时, 2. Case(3) Imax lnin Cmax A min =cnax Cmin A max 5) 2.2 2.0 其中Imx是电感和可变电容中的最大电流值 1.8 Case(1) (4)当Vk<Vr<Vc+Amax时,片上电感的FV 1.6 轨迹满足两个椭圆方程 1.49 00.20.40.60.81.0 V-V 2 2 Time/ns = ,V≥Vur 图2电感电容谐振回路的谐振电压波形 V-Va =1,V<Ve (6) Fig.2 Oscillation voltage waveforms at different Cmnax Cmin A max ECV voltages 其中 椭圆相似系数0满足1≤0≤Amx/Amn 上述四种情况也可以用片上电感的上V轨迹图 在上述四种情况下,谐振电路的谐振周期分别 来表示.图3说明了片上电感的上V轨迹是由两个 为 椭圆拼接而成.随着有效控制电压的变化,两个椭圆 (1)当Vdrk-Amm时,谐振周期 分别满足两个不同的椭圆方程 T Tmax =23t LCmax 7) (2)当Vrk+Amax时,谐振周期 T=Tain =2t NLCmin (8) 10 8 (3)当Vk-Amn<V<Vk时,谐振周期为两个 6 椭圆上的时间之和T=T+T2.T为在幅值Am的 4 椭圆上的时间,T2为在幅值0Ax的椭圆上的时间」 2 Amin 如图3所示,在交接点处片上电感上电压和电流分 V.-2.0V(case 1) 别是V和1a,求解(4)式中的两个方程,可以得到 -'.=2.5V(case 1) 椭圆相似系数日 =3.0V(case 1) =3.5V(case 1) 由(4)式的第一个椭圆方程可以得到 -10 lemr=士in CnaxAmin 1.41.61.82.02.22.42.62.83.03.23.43.6 Voltage/V 代入第二个椭圆方程得 图3谐振电路中片上电感的上V轨迹图 Vk·V正 Fig.3 FV locus of an omrchip inductor Amax (nax Cmin A max - 由(5)式有 (I)当Vk·Amm时,片上电感的上V轨迹 Amas 满足椭圆方程 (9) A min =1 (2 0= 10 Amax (2)当Vke+Amax时,片上电感的下V轨迹 可以计算出在两个椭圆上的时间分别为 满足椭圆方程 +sin Vde Ve (3) 2■
半 导 体 学 报 第 26 卷 ωmin ;在电压 V eff以下可变电容为最小电容值 Cmin ,振 荡波形是最大幅值 A max的正弦波形的一部分 ,频率 为最大频率ωmax . 图 2 电感2电容谐振回路的谐振电压波形 Fig. 2 Oscillation voltage waveforms at different ECV voltages 上述四种情况也可以用片上电感的 I2V 轨迹图 来表示. 图 3 说明了片上电感的 I2V 轨迹是由两个 椭圆拼接而成. 随着有效控制电压的变化 ,两个椭圆 分别满足两个不同的椭圆方程. 图 3 谐振电路中片上电感的 I2V 轨迹图 Fig. 3 I2V locus of an on2chip inductor (1) 当 V eff ≤V dc - A min时 ,片上电感的 I2V 轨迹 满足椭圆方程 V - V dc A min 2 + I ωmin Cmax A min 2 = 1 (2) (2) 当 V eff ≥V dc + A max时 ,片上电感的 I2V 轨迹 满足椭圆方程 V - V dc A max 2 + I ωmax Cmin A max 2 = 1 (3) (3) 当 V dc - A min < V eff < V dc时 ,片上电感的 I2V 轨迹满足两个椭圆方程 V - Vdc Amin 2 + I ωmin Cmax Amin 2 = 1 , V ≥Veff V - Vdc Amax 2 + I ωmax Cmin Amax 2 =θ2 , V < Veff 其中 椭圆相似系数θ满足 Amin / Amax ≤θ≤1. (4) 特别地 ,当有效控制电压 V eff = V dc ,椭圆相似系 数θ= 1 时 , Imax = ωmin Cmax A min = ωmax Cmin A max (5) 其中 Imax是电感和可变电容中的最大电流值. (4) 当 V dc < V eff < V dc + A max时 ,片上电感的 I2V 轨迹满足两个椭圆方程 V - Vdc Amin 2 + I ωmin Cmax Amin 2 =θ2 , V ≥Veff V - Vdc Amax 2 + I ωmax Cmin Amax 2 = 1 , V < Veff 其中 椭圆相似系数θ满足 1 ≤θ≤Amax / Amin . (6) 在上述四种情况下 ,谐振电路的谐振周期分别 为 (1) 当 V eff ≤V dc - A min时 ,谐振周期 T = Tmax = 2π LCmax (7) (2) 当 V eff ≥V dc + A max时 ,谐振周期 T = Tmin = 2π LCmin (8) (3) 当 V dc - A min < V eff < V dc时 ,谐振周期为两个 椭圆上的时间之和 T = T1 + T2 . T1 为在幅值 A min的 椭圆上的时间 , T2 为在幅值θA max的椭圆上的时间. 如图 3 所示 ,在交接点处片上电感上电压和电流分 别是 V eff和 Ieff ,求解(4) 式中的两个方程 ,可以得到 椭圆相似系数θ. 由(4) 式的第一个椭圆方程可以得到 Ieff = ±ωmin Cmax A min 1 - V dc - V eff A min 2 代入第二个椭圆方程得 θ2 = V dc - V eff A max 2 + ωmin Cmax A min ωmax Cmin A max 2 1 - V dc - V eff A min 2 由(5) 式有 A max A min = Cmax Cmin (9) θ= 1 - V dc - V eff A min 2 + V dc - V eff A max 2 (10) 可以计算出在两个椭圆上的时间分别为 T1 = π 2 + sin - 1 V dc - V eff A min π Tmax 2102

第10期 唐长文等:一种采用开关阶跃电容的压控振荡器(上):调谐特性的理论分析 2013 sin T Mp 则谐振周期为 V C T=T+T (b) -sin' (Tmax+Tmin) Mnl (c) (11) (a) (5)当Vk<Vr<Vke+Amax时,与第4种情况相 图4CMOS双端差分调谐压控振荡器()双端差分调谐压 同的方法,求解(6)式的两个方程可以得到椭圆相似 控振荡器电路图:(b)半电路等效电感电容串联回路:(c)正、负 系数8和谐振周期 阶跃可变电容CV曲线 2 V-Vs Fig.4 CMOS differentially-tuned LC-tank VCO (a) (12 A max Amin LC-tank VCO tuned by nMOS and pMOS varactors: (b)Simplified half circuit:(c)Positive-step and nega- T= (Ta+Tmim}+ 2 tive-step GV curves Veft-Vdc Tmax sin Cmax ,n V≥Vosn Cs.n(V) (13) Cmin,n y<Vos.n 14) C签p(V) CminP V≥VosP 3差分调谐的压控振荡器 Cmax p, V Vos.p 其中 Vs,a和Vsp分别nMOS管可变电容和 由于压控振荡器中共模噪声的存在,例如电源 pMOS管可变电容的CV曲线的偏移电压.nMOS 噪声、尾电流源噪声等,使得单端调谐的压控振荡器 管的有效控制电压为Vea=Vcin+'as,n,pMOS管 存在很大的邻近相位噪声.而与其他差分电路一样, 的有效控制电压为V脚=Vc中+Vosp· 差分调谐压控振荡器能够减小共模噪声的上变频过 图4(b)中串联谐振电路的谐振电压波形如图5 程.其次,差分调谐压控振荡器的调谐增益是单端调 所示,它是由三个正弦波形相拼接而成,转折点电压 谐的压控振荡器的一半,这样在降低相位噪声方面 为有效控制电压Vm和Vm.首先我们来看四种特 有很大优势].差分调谐压控振荡器如图4(a)所 殊的情况(见图5(a)~(d),这四种情况下的振荡 示,与单端调谐振荡器一样,两个片上电感的存在使 电压波形都是一个完整正弦波形 得差分振荡波形的直流分量是Vk,差分调谐的阶 (I)如图5(a)所示,当有效控制电压'urn,V 跃可变由正向阶跃的nMOS管可变电容和负向阶 都很低时,振荡器中的可变电容Csn始终为Cmn, 跃的pMOS管可变电容构成.忽略片上电感和可变 可变电容CsP始终为Cmm,P,总的电容为两个可变电 电容中的串联损耗电阻,压控振荡器的半电路可以 容之和Cmd=Cax,a十Cmnp,振荡器的幅度为Amdl, 看作为图4(b)中的串联电感电容谐振电路.nMOS 频率为id1; 管可变电容和pMOS管可变电容的CV曲线都可 (2)如图5(b)所示,当有效控制电压Va,Vm 以近似为一个阶跃函数(见图4(c) 都很高时,振荡器中的可变电容Csn始终为Cma, 正向阶跃的nMOS管可变电容和负向阶跃的 可变电容C“p始终为CmxP,总的电容为两个可变电 pMOS管可变电容分别为 容之和Cmdn=Cmn,n十Cmaxp,振荡器的幅度为Am2, 频率为4mn;
第 10 期 唐长文等 : 一种采用开关阶跃电容的压控振荡器(上) :调谐特性的理论分析 T2 = π 2 - sin - 1 V dc - V eff θA max π Tmin 则谐振周期为 T = T1 + T2 = π 2 + sin - 1 V dc - V eff A min π Tmax + π 2 - sin - 1 V dc - V eff θA max π Tmin = 1 2 ( Tmax + Tmin ) + 1 π sin - 1 V dc - V eff A min Tmax - sin - 1 V dc - V eff θA max Tmin (11) (5) 当 V dc < V eff < V dc + A max时 ,与第 4 种情况相 同的方法 ,求解(6) 式的两个方程可以得到椭圆相似 系数θ和谐振周期. θ= 1 - V eff - V dc A max 2 + V eff - V dc A min 2 (12) T = 1 2 ( Tmax + Tmin ) + 1 π - sin - 1 V eff - V dc θA min Tmax +sin - 1 V eff - V dc A max Tmin (13) 3 差分调谐的压控振荡器 由于压控振荡器中共模噪声的存在 ,例如电源 噪声、尾电流源噪声等 ,使得单端调谐的压控振荡器 存在很大的邻近相位噪声. 而与其他差分电路一样 , 差分调谐压控振荡器能够减小共模噪声的上变频过 程. 其次 ,差分调谐压控振荡器的调谐增益是单端调 谐的压控振荡器的一半 ,这样在降低相位噪声方面 有很大优势[ 6 ] . 差分调谐压控振荡器如图 4 (a) 所 示 ,与单端调谐振荡器一样 ,两个片上电感的存在使 得差分振荡波形的直流分量是 V dc . 差分调谐的阶 跃可变由正向阶跃的 nMOS 管可变电容和负向阶 跃的 pMOS 管可变电容构成. 忽略片上电感和可变 电容中的串联损耗电阻 ,压控振荡器的半电路可以 看作为图 4 (b) 中的串联电感2电容谐振电路. nMOS 管可变电容和 pMOS 管可变电容的 C2V 曲线都可 以近似为一个阶跃函数(见图 4 (c) ) . 正向阶跃的 nMOS 管可变电容和负向阶跃的 pMOS 管可变电容分别为 图 4 CMOS 双端差分调谐压控振荡器 (a) 双端差分调谐压 控振荡器电路图 ; (b) 半电路等效电感电容串联回路 ; (c) 正、负 阶跃可变电容 C2V 曲线 Fig. 4 CMOS differentially2tuned LC2tank VCO (a) LC2tank VCO tuned by nMOS and pMOS varactors; (b) Simplified half circuit ; (c) Positive2step and nega2 tive2step C2V curves Css ,n (V ) = Cmax ,n , V ≥Vos ,n Cmin ,n , V < Vos ,n Css ,p (V ) = Cmin ,p , V ≥Vos ,p Cmax ,p , V < Vos ,p (14) 其中 Vos ,n 和 Vos ,p 分 别 nMOS 管 可 变 电 容 和 pMOS 管可变电容的 C2V 曲线的偏移电压. nMOS 管的有效控制电压为 V effn = V ctrln + Vos ,n ,pMOS 管 的有效控制电压为 V effp = V ctrlp + Vos ,p . 图 4 (b) 中串联谐振电路的谐振电压波形如图 5 所示 ,它是由三个正弦波形相拼接而成 ,转折点电压 为有效控制电压 V effn和 V effp . 首先我们来看四种特 殊的情况(见图 5 (a) ~ ( d) ) ,这四种情况下的振荡 电压波形都是一个完整正弦波形. (1) 如图 5 (a) 所示 ,当有效控制电压 V effn ,V effp 都很低时 ,振荡器中的可变电容 Css ,n始终为 Cmax ,n , 可变电容 Css ,p始终为 Cmin ,p ,总的电容为两个可变电 容之和 Cmid1 = Cmax ,n + Cmin ,p ,振荡器的幅度为 A mid1 , 频率为ωmid1 ; (2) 如图 5 ( b) 所示 ,当有效控制电压 V effn ,V effp 都很高时 ,振荡器中的可变电容 Css ,n始终为 Cmin ,n , 可变电容 Css ,p始终为 Cmax ,p ,总的电容为两个可变电 容之和 Cmid2 = Cmin ,n + Cmax ,p ,振荡器的幅度为 A mid2 , 频率为ωmid2 ; 3102

2014 半导体学报 第26卷 3.5 35 T=T,=0 10 m=mp-3.13V 5 3.0 0 3.0 0 10 iaalo 2.5 A/)A 103 2.5 2.0 V.m-V-1.87V 2.0 -T-T T-T-=0 1.50020.40.60.81.012 1.50 0.20.40.60.81.01.2 Time/ns Time/ns (a) (b) 3.5 Vettn-3.5V 10 3.5 T=T=0 10 T=T=0 0 3.0 Locus Vemp=3.0V 3.0 Locus 85P 103 105 2.5 2.5 V.m=2.5V 2.0 2.0 T-T: Vemp=1.5V T=T,- 1.30 020.4 0.60.81.0 1.2 1.5002 0.4 0.60.8 1.012 Time/ns Time/ns (c) (d) 图5压控振荡器的四种特殊情况下的振荡波形和片上电感的上V轨迹图(a)Va,V师k·Amd;(b)Vm,Vmk· Amin;(c)Vcn女+Amx,V年t·Amax;(d)Vcnk-Amin,Vc面女+Amin Fig.5 Oscillation waveforms and FV loci in four special cases (a)Vom,vp-Amd (b)Vam,Vp a ·Amn;(c)Vnt+Ammx,'mk·Amx;(d)Vmt·Amn,Vmk+Amm (3)如图5(c)所示,当有效控制电压V很高, 的电压波形是三种不同大小的部分正弦波在有效控 V眸很低时,振荡器中的可变电容Cs,始终为 制电压点相拼接而成.根据两个有效控制电压V Cman,可变电容Csp始终为Cminp,总的电容为最小 和V的大小可以将所有压控过程划分为以下八种 电容值Cmn=Cmin,n十Cmin,振荡器的幅度为最大幅 情况: 度Aax,最大频率ax; (I)如图5(a)所示,当Vend-Amd1,且Ve (4)如图5(d)所示,当有效控制电压'm很低, k·Amd时,谐振回路的可变电容始终为Cmx,n V很高时,振荡器中的可变电容Csm始终为 +Cmnp,谐振波形是一个中等幅值Amd的正弦波, Cmx,n,可变电容Csp始终为CmxP,总的电容为最大 频率为nmdi. 电容值Cmx=Cax,n+CaxP,振荡器的幅度为最小幅 (2)如图6(a)所示,当Vunk,Vms,且 度Amn,最小频率n. Vn御时,在电压Vm以上的谐振波形是幅值 根据上述四种特殊情况下电感的上V轨迹图分 Amd的正弦波的部分,电容值为Cmdl=Cmx,a+ 析,可知这四种特殊情况下的正弦波幅度满足公式 Cmmp,频率为4dl;在电压Vca以下和电压Ve眸以上 Imax =midl Cmidl Amid1 =id2 Cmid Amid2 是幅值为AAx(?为椭圆比例系数)的正弦波的部 =amin Cmax A min =cmax Cmin A max 15) 分,电容值为Cmn=Cmin,n+Cmnp,频率为ax;在电 其中Imx是电感中的最大电流值 压V以下是幅值为?Am(?为椭圆比例系数)的 有效控制电压V和V使得阶跃可变电容在 正弦波的部分,电容值为Cmin=Cmn,a+Cnax p,频率 不同的电压上处于不同的电容值.差分调谐振荡器 (d2
半 导 体 学 报 第 26 卷 图 5 压控振荡器的四种特殊情况下的振荡波形和片上电感的 I2V 轨迹图 (a) V effn ,V effp ≤V dc - A mid1 ; (b) V effn ,V effp ≥V dc - A mid2 ; (c) V effn ≥V dc + A max ,V effp ≤V dc - A max ; (d) V effn ≤V dc - A min ,V effp ≥V dc + A min Fig. 5 Oscillation waveforms and I2V loci in four special cases (a) V effn ,V effp ≤V dc - A mid1 ; (b) V effn ,V effp ≥V dc - A mid2 ; (c) V effn ≥V dc + A max ,V effp ≤V dc - A max ; (d) V effn ≤V dc - A min ,V effp ≥V dc + A min (3) 如图 5 (c) 所示 ,当有效控制电压 V effn很高 , V effp很 低时 , 振 荡 器 中 的 可 变 电 容 Css ,n 始 终 为 Cmin ,n ,可变电容 Css ,p始终为 Cmin ,p ,总的电容为最小 电容值 Cmin = Cmin ,n + Cmin ,p ,振荡器的幅度为最大幅 度 A max ,最大频率ωmax ; (4) 如图 5 (d) 所示 ,当有效控制电压 V effn很低 , V effp很 高时 , 振 荡 器 中 的 可 变 电 容 Css ,n 始 终 为 Cmax ,n ,可变电容 Css ,p始终为 Cmax ,p ,总的电容为最大 电容值 Cmax = Cmax ,n + Cmax ,p ,振荡器的幅度为最小幅 度 A min ,最小频率ωmin . 根据上述四种特殊情况下电感的 I2V 轨迹图分 析 ,可知这四种特殊情况下的正弦波幅度满足公式 Imax = ωmid1 Cmid1 A mid1 = ωmid2 Cmid2 A mid2 = ωmin Cmax A min = ωmax Cmin A max (15) 其中 Imax是电感中的最大电流值. 有效控制电压 V effn和 V effp使得阶跃可变电容在 不同的电压上处于不同的电容值. 差分调谐振荡器 的电压波形是三种不同大小的部分正弦波在有效控 制电压点相拼接而成. 根据两个有效控制电压 V effn 和 V effp的大小可以将所有压控过程划分为以下八种 情况 : (1) 如图 5 (a) 所示 ,当 V effn ≤V dc - A mid1 ,且 V effp ≤V dc - A mid1 时 ,谐振回路的可变电容始终为 Cmax ,n + Cmin ,p ,谐振波形是一个中等幅值 A mid1 的正弦波 , 频率为ωmid1 . (2) 如图 6 (a) 所示 ,当 V effn ≤V dc ,V effp ≤V dc ,且 V effn ≥V effp 时 ,在电压 V effn 以上的谐振波形是幅值 A mid1 的正弦波的部分 ,电容值为 Cmid1 = Cmax ,n + Cmin ,p ,频率为ωmid1 ;在电压 V effn以下和电压 V effp以上 是幅值为θ1 A max (θ1 为椭圆比例系数) 的正弦波的部 分 ,电容值为 Cmin = Cmin ,n + Cmin ,p ,频率为ωmax ;在电 压 V effp以下是幅值为θ2 A mid2 (θ2 为椭圆比例系数) 的 正弦波的部分 ,电容值为 Cmid2 = Cmin ,n + Cmax ,p ,频率 ωmid2 . 4102