单色平面波的波动方程: E=Eo cos(ot-k+), 特点:单色平面波的振幅和传播方向均保持不变。 (2)波阵面或波面 波面
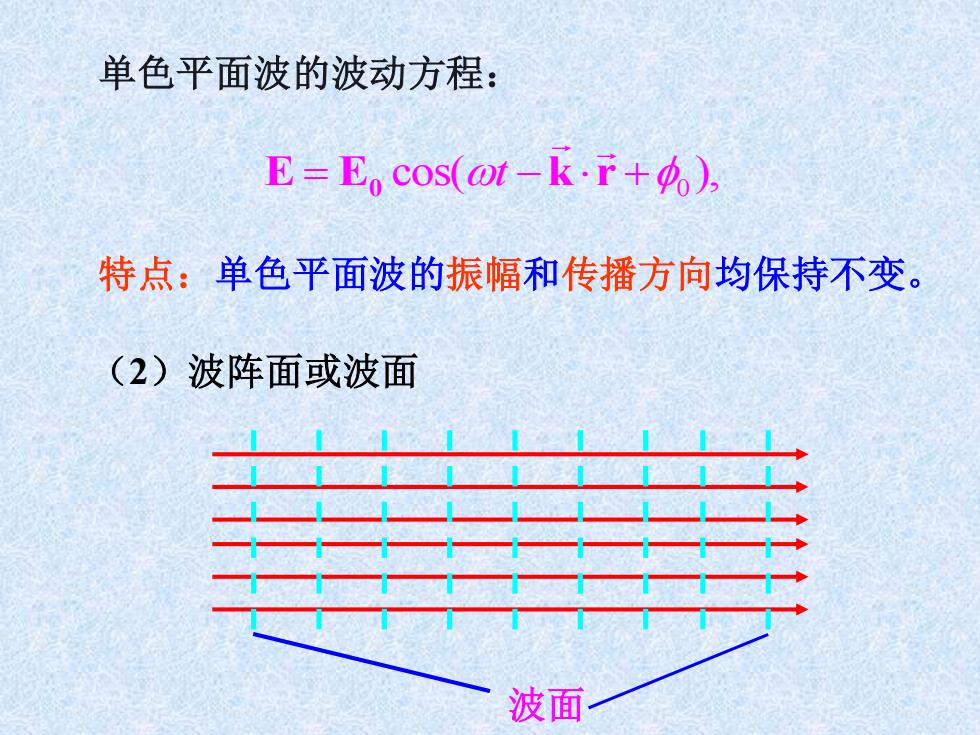
单色平面波的波动方程: cos( ), +0 E = E −k r 0 t 特点:单色平面波的振幅和传播方向均保持不变。 (2)波阵面或波面 波面

若平面波沿Z方向传播,则波动方程可表示为 E=Eo cos(ot-kz+), 2.单色球面波 从点光源发出的光在各向同性的均匀介质中传播, 其波面是以点光源为中心的球面,具有球对称性。 EA cos(o-kr) A:距点光源单位长距离处的光振幅
若平面波沿Z方向传播,则波动方程可表示为 cos( ), = − +0 t k z E E0 2. 单色球面波 从点光源发出的光在各向同性的均匀介质中传播, 其波面是以点光源为中心的球面,具有球对称性。 cos( ) 0 t k r r A E = − A0:距点光源单位长距离处的光振幅

即球面波的振幅与波传播的距 离r成反比。 补充:假设介质对光无吸收,根据能量守恒 4π21=4nr21或4πA=4πr24 4=4 令六单位长度,则4-4
O z y x Σ0 即球面波的振幅与波传播的距 Σ 离r成反比。 补充: 假设介质对光无吸收,根据能量守恒 r I r I 2 0 2 0 4 = 4 2 2 2 0 2 4 0 4 Ar 或 r A = r 0 0 r r A Ar = 令r0为单位长度,则 r A Ar 0 =

3.单色柱面波 柱面波是一个无限长的线光源 发出的光波,它的波面具有柱 面的形状。 三种单色波的波动方程可以统一写成: E=Acos(ot-无·r)
3. 单色柱面波 柱面波是一个无限长的线光源 发出的光波,它的波面具有柱 面的形状。 cos( ) 0 t k r r A E = − 三种单色波的波动方程可以统一写成: cos( ) ( ) E A t k r r = −

4.光波的复数表示形式 前面讲的是光波的一种数学描述方法,称为三角 函数表示法。为了运算方便,常把光波场的三角 函数表示式写成复数形式。 根据尤拉公式 exp(i)=cos0+isin 0 exp(-i0)=cos0-isin 0 三角函数cos0是复数exp(i0)或exp(-i0)的 实数部分,通常以符号R{野表示括号内复数Ψ的实 数部分
4. 光波的复数表示形式 前面讲的是光波的一种数学描述方法,称为三角 函数表示法。为了运算方便,常把光波场的三角 函数表示式写成复数形式。 根据尤拉公式 exp(i) = cos +isin exp(−i) = cos −isin 三角函数cos是复数exp(i )或exp(-i )的 实数部分,通常以符号Re {}表示括号内复数的实 数部分