
第四章 GNSS定位基本原理 式(4.2.6)中,δPm和δPom分别为对流层和电离层的 折射改正。设测站的近似坐标为(XpYp1Z,1) 其改正数为(6Xp1δ1δZn1),利用近似坐标将式 4.2.6)线性化可得伪距观测方程 +-”+ X91-X -Z d记,1-c-Pplo +(Bp+cot-prop-Opion+hplsin p)=0 (4.2.7) 式(4.2.7)中,(X,Y,Z)为卫星的瞬时坐标,而 V(X-X9)2+(Y-Y0)2+(Z-Z9)2 (4.2.8) 安徽理工大学导航定位技术应用研究所 U S 余学祥(0554)6633378xxyu9166@aliyun.com NPTAI
第四章 GNSS定位基本原理 式(4.2.6)中,δρtrop和δρion分别为对流层和电离层的 折射改正。设测站p1的近似坐标为(X0 p1 Y 0 p1 Z 0 p1), 其改正数为 (δXp1 δYp1 δZp1 ),利用近似坐标将式( 4.2.6)线性化可得伪距观测方程 sin ) 0 (4.2.7) ~ ( 1 1 1 1 1 1,0 1,0 0 1 1 1,0 0 1 1 1,0 0 1 + + − − + • = − − − + − + − i trop ion p p i i p i i p p p p i p i p p i p i p p i p c t h Z c t Z Z Y Y Y X X X 式(4.2.7)中,(X i ,Y i ,Z i)为卫星i的瞬时坐标,而 ( ) ( ) ( ) (4.2.8) 0 2 1 0 2 1 0 2 1,0 1 p i p i p i i p = X − X + Y −Y + Z − Z

第四章 GNSS定位基本原理 4.2.2载波相位测量的基本观测方程 以GS标准时为准,卫星在历元T发射的载波信号相位 为pφ(T),而测站p1的接收机在历元T1的参考载波信号相 位为pp1(Tp1,则相位差为 o(T)=p(T)-(T) (4.2.9 对于一个稳定性良好的振荡器来说,相位与频率之间有关 系 pt+△t)=p(t)+f·t (4.2.10) 式中,为信号频率,△为一微小时间间隔。则有 pn(Ti)=0'(T')+fT1-T') 于是由式(4.2.9)可得 Φ,(T)=p(Ti)-p'(T')=f(Ti-T')=ft1 (4.2.11)
第四章 GNSS定位基本原理 4.2.2 载波相位测量的基本观测方程 ( ) ( ) ( ) (4.2.9) 1 1 1 i i p p i p T = T − T 以GPS标准时为准,卫星i在历元T i发射的载波信号相位 为φi (T i ),而测站p1的接收机在历元Tp1的参考载波信号相 位为φp1 (Tp1 ),则相位差为 对于一个稳定性良好的振荡器来说,相位与频率之间有关 系 (t +t) =(t)+ f •t (4.2.10) 式中,f为信号频率,Δt为一微小时间间隔。则有 ( ) ( ) ( ) i p i i p1 Tp1 = T + f T 1 −T 于是由式(4.2.9)可得 ( ) ( ) ( ) ( ) (4.2.11) 1 1 1 1 1 i p i p i i p p i p T = T − T = f T −T = f •

第四章 GNSS定位基本原理 式(4.2.11)中的x是在卫星钟和接收机钟同步 的情况下,卫星信号的传播时间。由于卫星信号 的发射历元是未知的,因此需要根据已知的观测 历元t,(顾及对流层和电离层延迟改正)按下式计 算信号的传播时间: (4.2.12) 其中p为卫星与测站间的几何距离,p(dot)为 卫地距变率。 安徽理工大学导航定位技术应用研究所 余学祥(0554)6633378xxyu9166@aliyun.com NPTAI
式(4.2.11)中的τ是在卫星钟和接收机钟同步 的情况下,卫星信号的传播时间。由于卫星信号 的发射历元是未知的,因此需要根据已知的观测 历元t p1(顾及对流层和电离层延迟改正)按下式计 算信号的传播时间: ( ) (4.2.12) 1 1 ) 1 (1 1 1 1 1 1 p1 trop ion i p i p i p i p c t c c c = − − + + 其中ρ为卫星与测站间的几何距离,ρ(dot)为 卫地距变率。 第四章 GNSS定位基本原理
第四章 GNSS定位基本原理 由于卫星钟和接收机钟都不可避免地含有钟差的影响 ,在处理多测站多历元对不同卫星的同步观测结果时,必 须统一时间标准。由式(4.2.1)、(4.2.2)、(4.2.10 )及相位差的定义,可得卫星在历元发射的载波信号相 位p(ti),与测站p的在接收历元tn1的参考载波信号相位 Pp1(亿p1)之间的相位差为 ΦpI(tp1)=Φ1(T)+f(dp1-') (4.2.13) 考虑到式(4.2.11)有 安徽理工大学导航定位技术应用研究所 U S 余学祥(0554)6633378xxyu9166@aliyun.com NPTAI
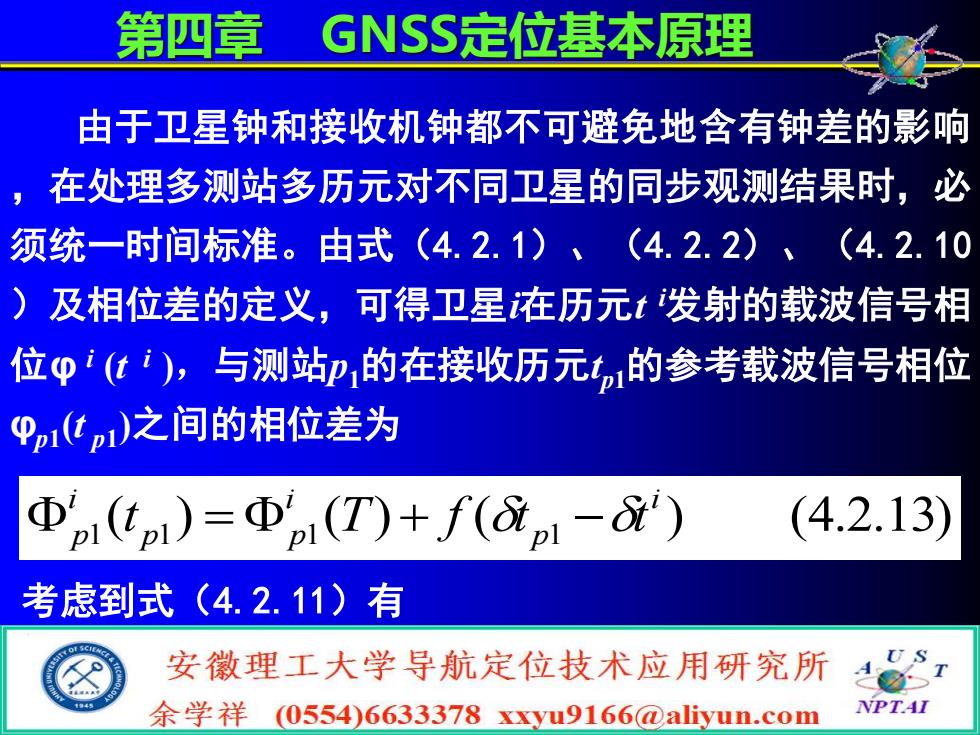
由于卫星钟和接收机钟都不可避免地含有钟差的影响 ,在处理多测站多历元对不同卫星的同步观测结果时,必 须统一时间标准。由式(4.2.1)、(4.2.2)、(4.2.10 )及相位差的定义,可得卫星i在历元t i发射的载波信号相 位φ i (t i ),与测站p1的在接收历元t p1的参考载波信号相位 φp1 (t p1 )之间的相位差为 ( ) ( ) ( ) (4.2.13) 1 1 1 1 i p i p p i p t = T + f t −t 考虑到式(4.2.11)有 第四章 GNSS定位基本原理

第四章 GNSS定位基本原理 Φn(i)=f●tl+f(d1-) (4.2.14 将式(4.2.12)代入式(4.2.14)得以观测历元为基础的载波 相位差 w,n)=p%0-p)+f0-2pa)du-f0+(⊙m+6a)(42.15) 因为通过测量接收机振荡器所产生的参考载波信号与 接收到的卫星载波信号之间的相位差,只能测定其不足二 整周的小数部分。若假设6p1(亿,)人、N1(t。)为起始历元t0 时相位差的小数部分及整周数,则起始历元时的总相位 差为 D,1(,)=9,1(Go)+Ni(4) (4.2.16 安徽理工大学导航定位技术应用研究所 余学祥 (0554)6633378 xxyu9166@aliyun.com NPTAI
( ) ( ) (4.2.14) 1 1 1 1 i p i p p i p t = f • + f t −t 将式(4.2.12)代入式(4.2.14)得以观测历元为基础的载波 相位差 ) ( ) (4.2.15) 1 ) (1 1 1 ( 1 ) 1 (1 1 1 1 trop ion i p i p i p i p p i p c f t f t c f c c f t = − + − − + + 因为通过测量接收机振荡器所产生的参考载波信号与 接收到的卫星载波信号之间的相位差,只能测定其不足一 整周的小数部分。若假设δφi p1 (t 0 )、N i p1 (t 0 )为起始历元t 0 时相位差的小数部分及整周数,则起始历元t 0时的总相位 差为 ( ) ( ) ( ) (4.2.16) 1 0 1 0 1 0 t t N t i p i p i p = + 第四章 GNSS定位基本原理