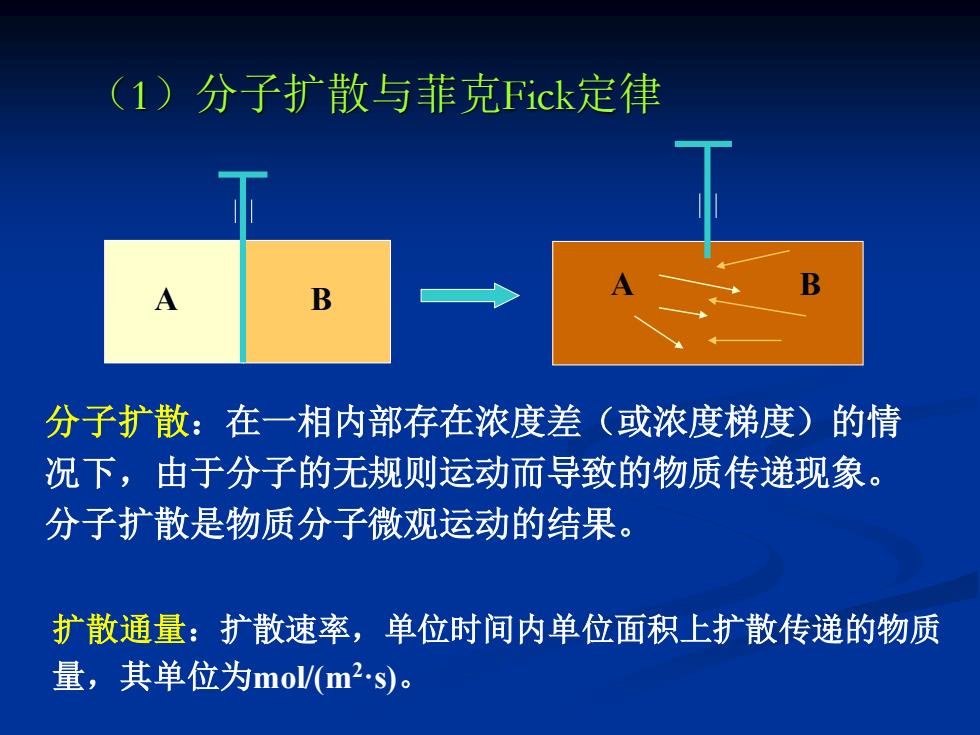
AA B B A B A B 分子扩散:在一相内部存在浓度差(或浓度梯度)的情 况下,由于分子的无规则运动而导致的物质传递现象。 分子扩散是物质分子微观运动的结果。 扩散通量:扩散速率,单位时间内单位面积上扩散传递的物质 量,其单位为mol/(m2·s)。 (1)分子扩散与菲克Fick定律
AA B B A B A B 分子扩散:在一相内部存在浓度差(或浓度梯度)的情 况下,由于分子的无规则运动而导致的物质传递现象。 分子扩散是物质分子微观运动的结果。 扩散通量:扩散速率,单位时间内单位面积上扩散传递的物质 量,其单位为mol/(m2·s)。 (1)分子扩散与菲克Fick定律

dz dC J D A A = − AB 式中 JA——物质A在z方向上的分子扩散通量,kmol/(m2 s) dCA/dz——物质A的浓度梯度,kmol/m4 DAB——物质A在介质B中的分子扩散系数,m2 /s 负号——表示扩散是沿着物质A浓度降低的方向进行的。 当物质A在介质B中发生扩散时,任一点处物质A的扩散通 量与该位置上A的浓度梯度成正比,即: 菲克(Fick)定律
dz dC J D A A = − AB 式中 JA——物质A在z方向上的分子扩散通量,kmol/(m2 s) dCA/dz——物质A的浓度梯度,kmol/m4 DAB——物质A在介质B中的分子扩散系数,m2 /s 负号——表示扩散是沿着物质A浓度降低的方向进行的。 当物质A在介质B中发生扩散时,任一点处物质A的扩散通 量与该位置上A的浓度梯度成正比,即: 菲克(Fick)定律
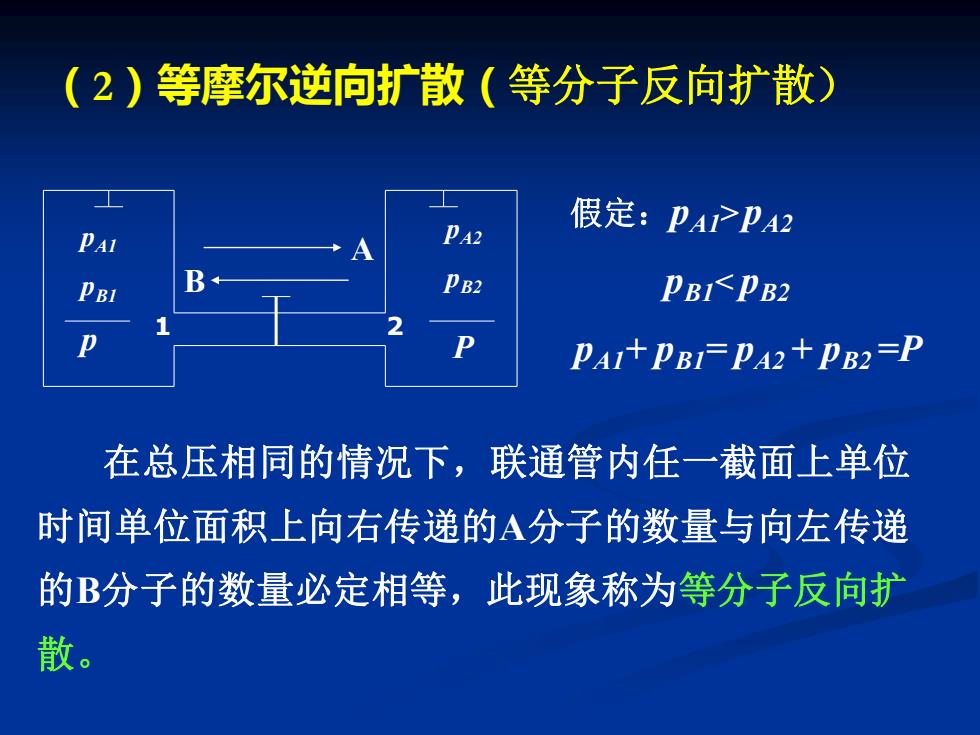
假定:pA1> pA2 pB1< pB2 pA1+ pB1= pA2 + pB2 =P pA1 pB1 pA2 pB2 p P A B 1 2 在总压相同的情况下,联通管内任一截面上单位 时间单位面积上向右传递的A分子的数量与向左传递 的B分子的数量必定相等,此现象称为等分子反向扩 散。 (2)等摩尔逆向扩散(等分子反向扩散)
假定:pA1> pA2 pB1< pB2 pA1+ pB1= pA2 + pB2 =P pA1 pB1 pA2 pB2 p P A B 1 2 在总压相同的情况下,联通管内任一截面上单位 时间单位面积上向右传递的A分子的数量与向左传递 的B分子的数量必定相等,此现象称为等分子反向扩 散。 (2)等摩尔逆向扩散(等分子反向扩散)

在任一固定的空间位置垂直于扩散方向的截面上,单位时 间通过单位面积的A物质的量,称为A的传递速率,以NA表示。 对于等分子反向扩散 JA= - JB 对于单纯的等分子反向扩散,物质A的传递速率应等于A的 扩散通量。 dz dp RT D dz dC N J D A A A = A = − = − 注意:在上述条件下,扩散为稳定过程,NA为常数; pA—z呈线性关系
在任一固定的空间位置垂直于扩散方向的截面上,单位时 间通过单位面积的A物质的量,称为A的传递速率,以NA表示。 对于等分子反向扩散 JA= - JB 对于单纯的等分子反向扩散,物质A的传递速率应等于A的 扩散通量。 dz dp RT D dz dC N J D A A A = A = − = − 注意:在上述条件下,扩散为稳定过程,NA为常数; pA—z呈线性关系

上式分离变量并积分, 积分条件为:z1=0,pA=pA1;z2=z,pA=pA2 ( ) A pA1 pA2 RTz D N = − P pA1 pB1 z1 P pB2 pA2 z2
上式分离变量并积分, 积分条件为:z1=0,pA=pA1;z2=z,pA=pA2 ( ) A pA1 pA2 RTz D N = − P pA1 pB1 z1 P pB2 pA2 z2