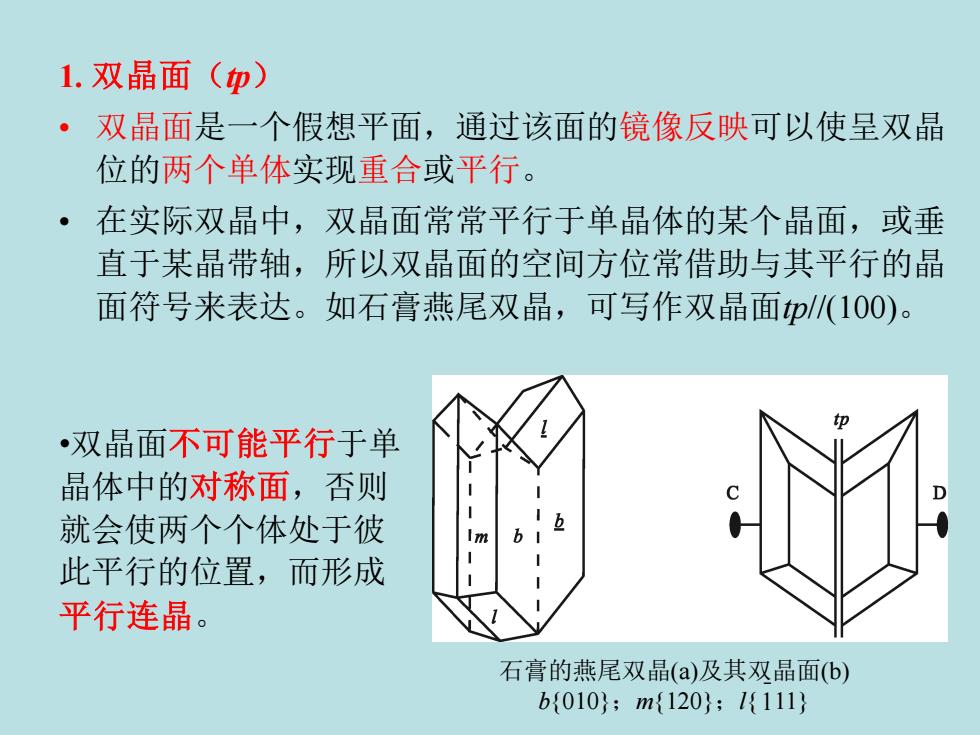
1.双晶面(tp)双晶面是一个假想平面,通过该面的镜像反映可以使呈双晶位的两个单体实现重合或平行在实际双晶中,双晶面常常平行于单晶体的某个晶面,或垂直于某晶带轴,所以双晶面的空间方位常借助与其平行的晶面符号来表达。如石膏燕尾双晶,可写作双晶面tp//(100)。tp·双晶面不可能平行于单晶体中的对称面,否则h就会使两个个体处于彼Im此平行的位置,而形成平行连晶石膏的燕尾双晶(a)及其双晶面(b)b(010):m/120):1(111)
1. 双晶面(tp) • 双晶面是一个假想平面,通过该面的镜像反映可以使呈双晶 位的两个单体实现重合或平行。 • 在实际双晶中,双晶面常常平行于单晶体的某个晶面,或垂 直于某晶带轴,所以双晶面的空间方位常借助与其平行的晶 面符号来表达。如石膏燕尾双晶,可写作双晶面tp//(100)。 •双晶面不可能平行于单 晶体中的对称面,否则 就会使两个个体处于彼 此平行的位置,而形成 平行连晶。 石膏的燕尾双晶(a)及其双晶面(b) b{010};m{120};l{ 11} − 1

日(tl)2.双晶轴,双晶轴为一假想直线,假设双晶的一个单体不动另一个单体围绕该直线旋转一定角度后(一般是180°),可与该单体重合或平行双晶轴总是垂直于单晶体的某个晶面,或平行于其中一个单晶体的某些晶棱或晶带轴,所以双晶轴的空间方位也借用与其垂直的晶面或平行的晶带轴的符号来表示。如,石膏燕尾双晶的双晶轴tl (100)。基转角为180°的双晶轴不能平行于单晶体的偶次轴,否则也将会形成平行连生
2. 双晶轴(tl) • 双晶轴为一假想直线,假设双晶的一个单体不动, 另一个单体围绕该直线旋转一定角度后(一般是 180º),可与该单体重合或平行。 • 双晶轴总是垂直于单晶体的某个晶面,或平行于 其中一个单晶体的某些晶棱或晶带轴,所以双晶 轴的空间方位也借用与其垂直的晶面或平行的晶 带轴的符号来表示。如,石膏燕尾双晶的双晶轴 tl⊥(100)。 • 基转角为180º的双晶轴不能平行于单晶体的偶次 轴,否则也将会形成平行连生

双晶要素石膏双晶面 P双晶轴BCA
石膏 双晶面 P 双晶轴 双晶要素

3.双晶中心(tc),双晶中心为一假想的几何点,通过该点将双晶中的一个晶体进行反伸操作后,两个单体实现相互重合或平行双晶中心只有在没有对称中心的晶体中出现,否则也将形成平行连生。,注:在实际的双晶分析中很少用到。双晶中可能存在的双晶面和双晶轴不止一个。一个双晶中单体间的取向关系只需描述其中一个双晶面或双晶轴就能确定,其他双晶要素往往省略
3. 双晶中心(tc) • 双晶中心为一假想的几何点,通过该点将双晶中的一个晶 体进行反伸操作后,两个单体实现相互重合或平行。 • 双晶中心只有在没有对称中心的晶体中出现,否则也将形 成平行连生。 • 注:在实际的双晶分析中很少用到。 • 双晶中可能存在的双晶面和双晶轴不止一个。一个双晶中 单体间的取向关系只需描述其中一个双晶面或双晶轴就能 确定,其他双晶要素往往省略