
U K 积分可得杆的总变形能 -2 2E1 2GI, 注:1)上式中忽略了剪切变形能 2) 若为非圆截面杆,则扭转变形能中的。 应改为4; 3)不同内力分量引起的变形能可以叠加, 同一内力分量的变形能不能叠加。 17
17 积分可得杆的总变形能 = l EA N x x U 2 ( )d 2 + l GI p T x x 2 ( )d 2 + l EI M x x 2 ( )d 2 注:1) 上式中忽略了剪切变形能; 2) 若为非圆截面杆,则扭转变形能中的I p 应改为I t ; 3) 不同内力分量引起的变形能可以叠加, 同一内力分量的变形能不能叠加
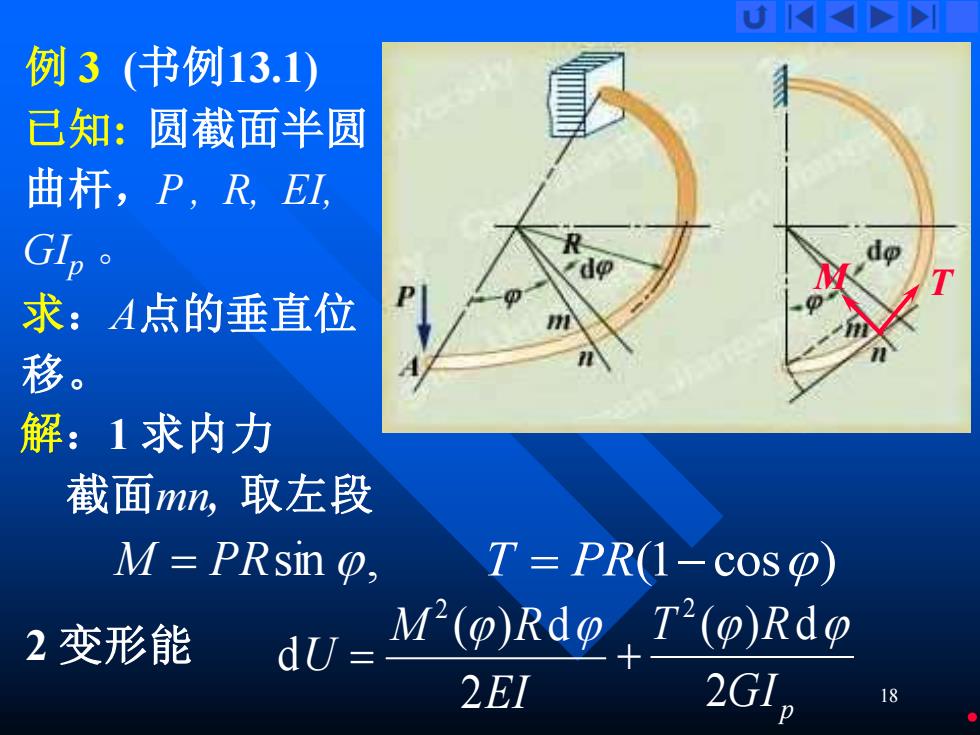
U K 例3(书例13.1) 己知:圆截面半圆 曲杆,P,REI, GL,° 求:A点的垂直位 移。 解:1求内力 截面mn,取左段 M=PRsin T=PR(1-cos) 2变形能 dU= M(p)Rdo T"(p)Rdp 2EI 2G1p 18
18 例 3 (书例13.1) 已知 : 圆截面半圆 曲杆,P , R, EI, GIp 。 求 : A点的垂直位 移。解:1 求内力 截面mn, 取左段 M T M = PRsin , T = PR ( 1 − cos ) 2 变形能 EI M R U 2( ) d d 2 = GI p T R 2( ) d 2 +
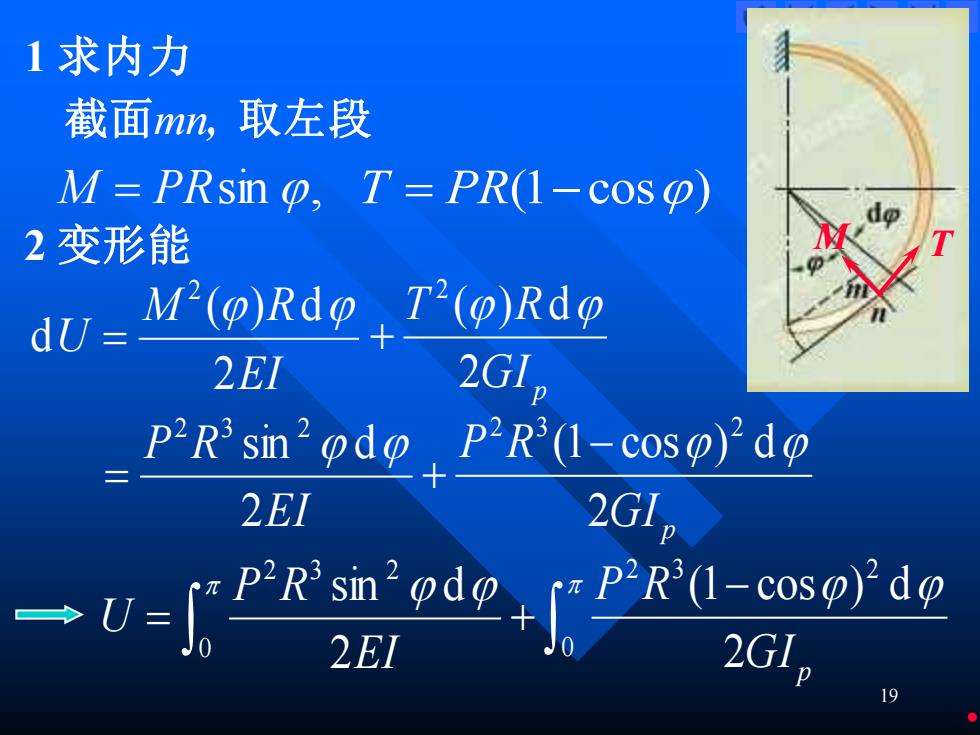
1求内力 截面mn, 取左段 M=PRsin p,T=PR(1-cosp) 2变形能 dU M'(P)Rdo T(o)Rdp 2EI 2G1, PRs P2R(1-coso)2do 2E1 2G1, 一r-rP0ePR0:a8e 2EI 2G1
19 1 求内力 截面mn, 取左段 M = PRsin , T = PR(1− cos) 2 变形能 EI M R U 2 ( ) d d 2 = GI p T R 2 ( ) d 2 + M T EI P R 2 sin d 2 3 2 = GI p P R 2 (1 cos ) d 2 3 2 − + = 0 2 3 2 2 sin d EI P R U − + 0 2 3 2 2 (1 cos ) d GI p P R

U KK --产02-r00 2GIp p2Rπ,3P2R3元 4E1 4G1, 3外力的功 W=2P8 由U=W,得: 2 do P2Rπ 3P2Rπ 2 4EI 4G1, 3PRπ δ4 PRπ, 2EI 2G1, 20
20 = 0 2 3 2 2 sin d EI P R U − + 0 2 3 2 2 (1 cos ) d GI p P R EI P R 4 2 3 = GI p P R 4 3 2 3 + 3 外力的功 W P A 2 1 = 由U=W,得: P A = 2 1 EI P R 4 2 3 GI p P R 4 3 2 3 + EI PR A 2 3 = GI p PR 2 3 3 +

作业 0第4版 013.1,13.3b),(c 21
21 作业 第4版 13.1, 13.3(b),(c)