
三、通过平壁的导热 1.单层平壁 如图所设,且假定入为常数, 则将一维稳态条件用于傅立叶定律: 9s- 1+dt 9s-1t dt 所以 9 本=-=cont ,t与X成线性关系。 或 qdx =-Adt 沿x方向定积分,得 6qc=-∫dn 而由一维稳态条件,知q与x无关, (d0=d0,q,=9=9, d02.) do do ds ds h 所以q哈d=-d 所以9=-5) 而 9s96 ds 所以d0=2.4-s b —单层平壁微分导热公式 沿平面定积分,得 0=或gs=分s b 所以Q=S.1-飞 一单层平壁导热公式 b
三、 通过平壁的导热 1.单层平壁 如图所设,且假定为常数, 则将一维稳态条件用于傅立叶定律: 得 所以 ,t与x成线性关系。 或 沿x方向定积分,得 而由一维稳态条件,知q与x无关, ( ) 所以 所以 而 所以 ——单层平壁微分导热公式 沿平面定积分,得 所以 ——单层平壁导热公式 z, t O x dx x b 1 t 2 t t t +dtdS n t q = − dx dt q = − const q dx dt = − = qdx = −dt = − 2 1 0 t t b qdx dt dS dQ q dS dQ dQ dQ q 2 2 1 1 2 1 = , = = = = − 2 1 0 t t b q dx dt b t t q ( ) 1 − 2 = dS dQ q = dS b t t dQ − = 1 2 − = − = Q S S dS b t t dS b t t dQ 0 1 2 0 1 2 0 b t t Q S 1 − 2 = b 1 dQ 2 dQ
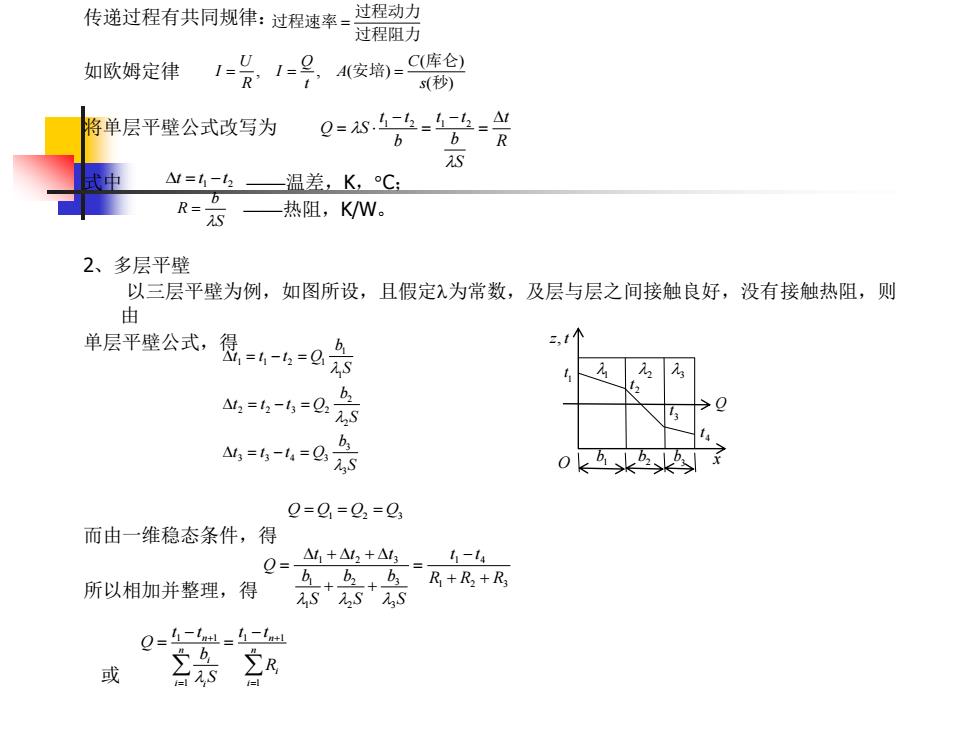
传递过程有共同规律:过程速率=过程动力 过程阻力 如欧姆定律 R 1=g 4(安培)=C库仑 s(秒) 将单层平壁公式改写为 Q=S.-6=-点-4 b b R AS 式中 M=4-2一温差,K,C: R=b —热阻,K/W。 S 2、多层平壁 以三层平壁为例,如图所设,且假定入为常数,及层与层之间接触良好,没有接触热阻,则 由 单层平壁公式, 很-4-5=0 b ,1个 △12=12-=Q2 12S >o A43=5-4=0 b S 0b≥6x 0=g=02=0 而由一维稳态条件,得 =A+A山,+A4,=1- 所以相加并整理,得 景+念+套+品+R Q=-=4-烈 或 籍风 l
传递过程有共同规律: 如欧姆定律 将单层平壁公式改写为 式中 ——温差,K,C; ——热阻,K/W。 2、多层平壁 以三层平壁为例,如图所设,且假定为常数,及层与层之间接触良好,没有接触热阻,则 由 单层平壁公式,得 而由一维稳态条件,得 所以相加并整理,得 或 ( ) ( ) , , ( ) 秒 库仑 安培 s C A t Q I R U I = = = 过程阻力 过程动力 过程速率 = R t S b t t b t t Q S = − = − = 1 2 1 2 1 2 t = t −t S b R = S b t t t Q S b t t t Q S b t t t Q 3 3 3 3 4 3 2 2 2 2 3 2 1 1 1 1 2 1 = − = = − = = − = Q = Q1 = Q2 = Q3 1 2 3 1 4 3 3 2 2 1 1 1 2 3 R R R t t S b S b S b t t t Q + + − = + + + + = = + = + − = − = n i i n n i i i n R t t S b t t Q 1 1 1 1 1 1 b1 b2 3 b 1 t 2 t 3 t 4 t z, t O x Q 1 2 3
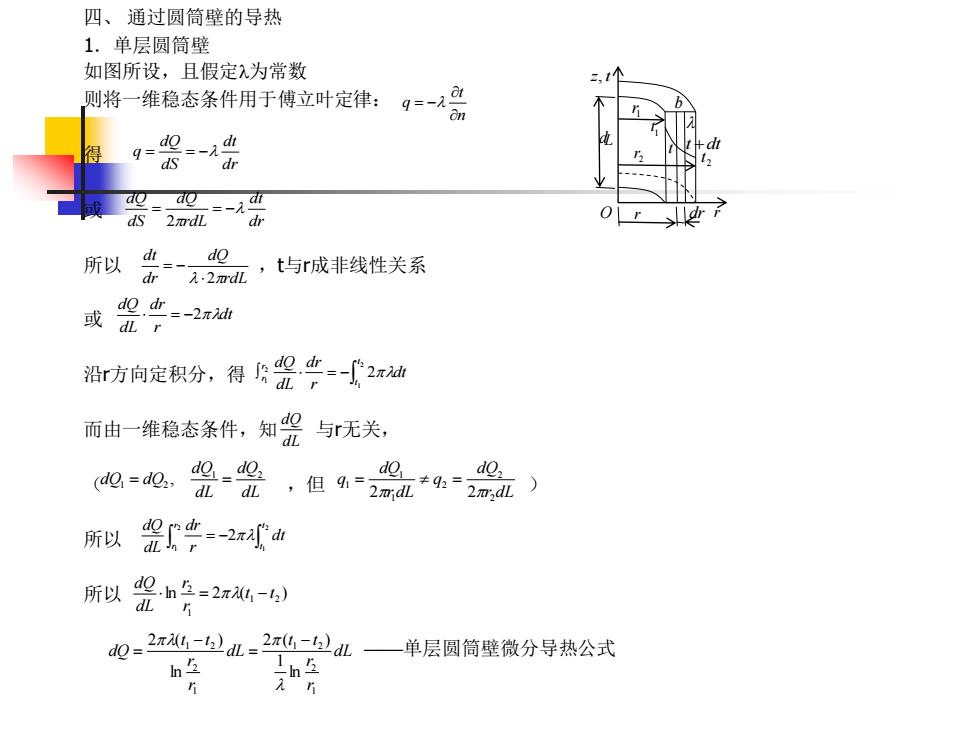
四、通过圆筒壁的导热 1.单层圆筒壁 如图所设,且假定为常数 则将一维稳态条件用于傅立叶定律:q=- On 得 9s9. ds dr dS 2mdL dr 所以-a№ t与r成非线性关系 d迴.d=-2x 或dLr 沿r方向定积分,得片皇中-2x灿 而由一维稳态条件,知9与r无关, dl. 电=0.光-是,但=2照 do do, 2m2d) 所以架中2 所以架冬2- d0=2m-2dL=2-dL一单层圆筒壁微分导热公式 In
四、 通过圆筒壁的导热 1.单层圆筒壁 如图所设,且假定为常数 则将一维稳态条件用于傅立叶定律: 得 或 所以 ,t与r成非线性关系 或 沿r方向定积分,得 而由一维稳态条件,知 与r无关, ( ,但 ) 所以 所以 ——单层圆筒壁微分导热公式 n t q = − dr dt dS dQ q = = − dr dt rdL dQ dS dQ = = − 2 rdL dQ dr dt 2 = − dt r dr dL dQ = −2 = − 2 1 2 1 2 t t r r dt r dr dL dQ dL dQ r dL dQ q r dL dQ q 2 2 2 1 1 1 2 2 = = dL dQ dL dQ dQ dQ 1 2 1 2 = , = = − 2 1 2 1 2 r r t t dt r dr dL dQ ln 2 ( ) 1 2 1 2 t t r r dL dQ = − dL r r t t dL r r t t dQ 1 2 1 2 1 2 1 2 ln 1 2 ( ) ln 2 ( ) − = − = z, t O r 1 t 2 t t t +dt 1 r 2 r r dr L b d

整理d0=.2n-2.4- 2πdL5 - 2ndLr d0=元,_.4-业=元.-5s. 单层圆筒壁微分导热公式 nS⅓-万 b ds 式中dS=2-a In ds 一对数平均微元面积,m2; ds 当dS,=dS2 时SM=dS1=dS2 沿柱面定积分,得 do-2-d-2fa h h 所以 0=2La=2_24-2 h专 h 一单层圆筒壁导热公式 5 整理 0=元.2%-2.1-4 h22-5 2xLn Q=S-3.-6=545=4= h当5-5 单层圆筒壁导热公式 b b R AS 式中 S=S-S 一对数平均面积,m2S当2 Sm时=S2 S △1=41-42 一温差,K,C R= —热阻,KWW
整理 ——单层圆筒壁微分导热公式 式中 ——对数平均微元面积,m2; 当 时 , 。 沿柱面定积分,得 所以 ——单层圆筒壁导热公式 整理 ——单层圆筒壁导热公式 式中 ——对数平均面积,m2;当 时, 。 ——温差,K,C; ——热阻,K/W。 2 1 1 2 1 2 2 1 2 2 ln 2 ( ) r r t t dLr dLr dL r r dQ − − − = dSm b t t r r t t dS dS dS dS dQ − = − − − = 1 2 2 1 1 2 1 2 2 1 ln 1 2 2 1 ln dS dS dS dS dSm − = dS1 = dS2 dSm = dS1 = dS2 − = − = Q L L dL r r t t dL r r t t dQ 0 1 2 1 2 0 1 2 1 2 0 ln 2 ( ) ln 2 ( ) 1 2 1 2 1 2 1 2 ln 1 2 ( ) ln 2 ( ) r r L t t r r L t t Q − = − = 2 1 1 2 1 2 2 1 2 2 ln 2 ( ) r r t t Lr Lr L r r Q − − − = R t S b t t b t t S r r t t S S S S Q m m = − = − = − − − = 1 2 1 2 2 1 1 2 1 2 2 1 ln 1 2 2 1 ln S S S S Sm − = S1 = S2 Sm = S1 = S2 1 2 t = t −t S b R =

课堂练习:设 入=。+at,试求单层圆筒壁的导热传热速率计算公式。 解:由9=-号 得 9= do dr dr do dr=2d dL r 沿r方向定积分,得 片2女2灿 器华-2af话+mh 所以 40.in52mkv+ae dL r h生=-226-0+号6-0 dL =22+a-4) 2 2l2+a1t 2 4-42) 得Q= 2l(+ai4-4)_2万4-2) In h点 h发 所以当,与t成线性关系时,只要将导热公式中的,用算术平均温度下的代替,即可 求解变导热系数的导热问题。否则,要用积分平均值代替
课堂练习:设 ,试求单层圆筒壁的导热传热速率计算公式。 解:由 得 沿r方向定积分,得 所以 得 所以当与t成线性关系时,只要将导热公式中的用算术平均温度下的代替,即可 求解变导热系数的导热问题。否则,要用积分平均值代替。 = + at 0 n t q = − dr dt dS dQ q = = − dr dt rdL dQ dS dQ = = − 2 dt r dr dL dQ = −2 = − 2 1 2 1 2 t t r r dt r dr dL dQ = − + 2 1 2 1 2 ( ) 0 r r t t at dt r dr dL dQ 2 1 ) 2 ln 2 ( 2 0 1 2 t t t a t r r dL dQ = − + ( ) 1 2 1 2 0 2 1 2 0 2 1 2 1 2 2 2 ( ) 2 ln 2 ( ) t t t t a t t a t t r r dL dQ − + = + = − − + − 1 2 1 2 1 2 0 1 2 1 2 1 2 1 2 0 ln 2 ( ) ln 2 ( )( ) ln ( ) 2 2 r r L t t r r L at t t r r t t t t L a Q − = + − = − + + =