评价标准 成锁构成 评价方式 评价依据 主要考核学生对每章节知识点的复习、理解和掌握程 课后作业 度, 每次作业单独评分, 每周检查作业1次,占平时 成绩60%。 平时成绩 主要考核学生对所学知识的理解能力及应用所学知识 (20%30%) 课堂交流 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩20% 出勤及随机 主要考核学生出勤情况及对当堂课程的接受能力,占 测验 平时成绩20% 期末老试 主要题型有填空题、选择题、计算题和综合题等。其 (70%~80%) 闭卷考试 中,基础知识题约占70%,能力题约占30%。 三、教学内容及要求 高等数学A1 教学 对应的 章节 主要内容 教学要求 学时 方法和手段 课稻 课内课后 目标 正确理解函数的概念、奇偶性 单调性、周期性和有界性。 正确理解复合函数、反函数 概念,会进行函数的复合运算。 3、熟悉基本初等函数的性质及 1函数 2吸限 图 会建立简单实际问题中的函数 3极限的性质关系式。 与运算 5、正确理解极限的概念:掌握极 14极限存在准 限四则运算法则:会求有理函数 测和两个重要 限 理论教 复习初 等数学 一章 6、正确理解两个极限存在准则 学12 函数与 1.5无穷小的比 了解用极限存在准则求极限的方 的有关 学时 1、2、3 知识 极限 法:掌握两个重要极限,并会运用 习顺设 1.6函数的连 两个重要极限求极限 2学时 完成课 与间断 正确理解无穷小量和无穷大 后作业 17闭区间上连的概念,掌握无穷小量的性质以及 续函数的性质 无穷小量阶的比较:孰采常用的 穷小量等价关系 并会运用无穷 量等价代换求极限。 8、正确理解函数在一占左连娃 右连续、连续和间断的概念,并会 判别函数的间断点及其类型 熟卷初等函数的连续性和闭 间上连续函数的性质。 21
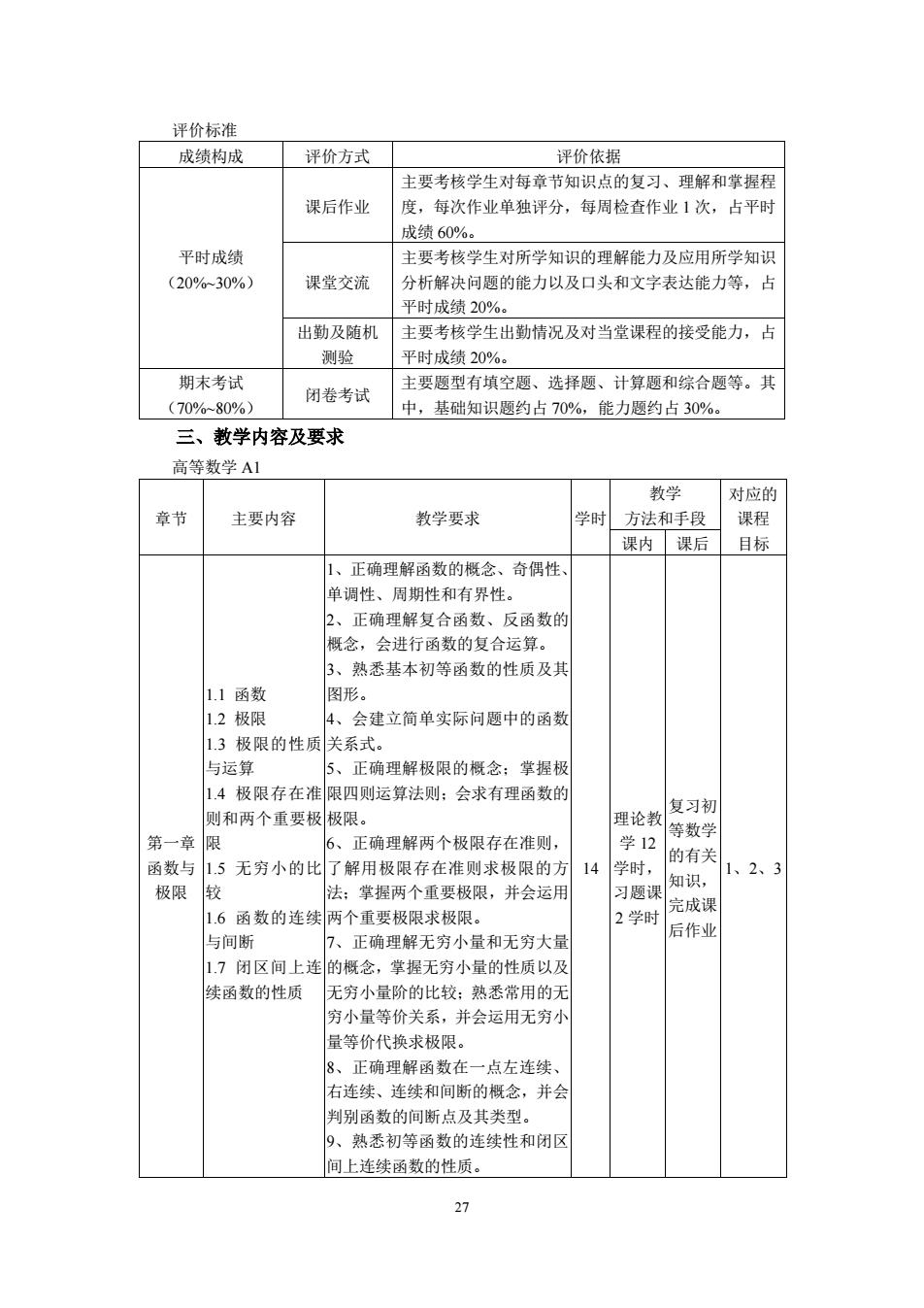
27 评价标准 成绩构成 评价方式 评价依据 平时成绩 (20%~30%) 课后作业 主要考核学生对每章节知识点的复习、理解和掌握程 度,每次作业单独评分,每周检查作业 1 次,占平时 成绩 60%。 课堂交流 主要考核学生对所学知识的理解能力及应用所学知识 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩 20%。 出勤及随机 测验 主要考核学生出勤情况及对当堂课程的接受能力,占 平时成绩 20%。 期末考试 (70%~80%) 闭卷考试 主要题型有填空题、选择题、计算题和综合题等。其 中,基础知识题约占 70%,能力题约占 30%。 三、教学内容及要求 高等数学 A1 章节 主要内容 教学要求 学时 教学 方法和手段 对应的 课程 课内 课后 目标 第一章 函数与 极限 1.1 函数 1.2 极限 1.3 极限的性质 与运算 1.4 极限存在准 则和两个重要极 限 1.5 无穷小的比 较 1.6 函数的连续 与间断 1.7 闭区间上连 续函数的性质 1、正确理解函数的概念、奇偶性、 单调性、周期性和有界性。 2、正确理解复合函数、反函数的 概念,会进行函数的复合运算。 3、熟悉基本初等函数的性质及其 图形。 4、会建立简单实际问题中的函数 关系式。 5、正确理解极限的概念;掌握极 限四则运算法则;会求有理函数的 极限。 6、正确理解两个极限存在准则, 了解用极限存在准则求极限的方 法;掌握两个重要极限,并会运用 两个重要极限求极限。 7、正确理解无穷小量和无穷大量 的概念,掌握无穷小量的性质以及 无穷小量阶的比较;熟悉常用的无 穷小量等价关系,并会运用无穷小 量等价代换求极限。 8、正确理解函数在一点左连续、 右连续、连续和间断的概念,并会 判别函数的间断点及其类型。 9、熟悉初等函数的连续性和闭区 间上连续函数的性质。 14 理论教 学 12 学时, 习题课 2 学时 复习初 等数学 的有关 知识, 完成课 后作业 1、2、3

正确理解导数和微分的概念 几何意义,熟悉函数可导性与连 性的关系,会用导数和微分的定义 求简单函数的导数和微分。 2、掌握导数的四则运算法则、复 合函数和反函数的求导法则, 掌握基本初等函数的导数及微分 公式:掌握微分的四则运算法则, 了解一阶微分形式不变性:会用求 导法则和求导公式计算初等函 21导数的概念 的导数或微分。 22求导法则 3、正确理解高阶导数的概念:会 23高阶导数与求函教的二阶、三阶导数和一些封 相关变化率 简单函数的n阶导数 2.4函数的微 会求隐函数和由参数方程所矿 在理论 第二章 25洛必达法则 定的函数的导数和高阶导数。 理论教 学习的 元函26微分中值定5、正确理解罗尔定理、拉格朗 学26 中值定理、柯西中值定理和泰勒叫 基 30 完成课 1、2 值定理,并会应用中值定理求解 后作 应用 2.8利用导数石 证明简单的中值问题。 4学时 业: 究函数的性态 、正确理解函数极值的概念和到 2.9平面曲线 别条件:掌握用导数判断函数的车 曲率 调性和求极值的方法:会判断函 的单调性,会求函数的极值。 7、会用导数判断函数图形的凹石 会求拐点:了解描绘函数的 线);会求解较简单的最大值和最 小值的应用问题。 8、正确理解罗必达法则,会用罗 必达法则求不定式的极限 9、了解曲线的曲率和曲率半径 概念,并会计算函数曲线的曲率和 曲率半 3.1定积分的概 正确理解不定积分的概念及超 今和性岳 在理论 第二 相论5 32微积分基本 堂据不定积分的基知分公式 函 定理 会用换元积分法和分部积分法 学2 学习的 数积 基础 33不定积分 学及 算不定积分:了解有理函数的积分 32 学时。 1、2、3 完成误 4定积分的 方法,会计算简单有理函数的不定 习趣 应用 4学时 后作 分 业 3.5 定积分应用3 正确理解定积分的概念及性质
28 第二章 一元函 数微分 学及其 应用 2.1 导数的概念 2.2 求导法则 2.3 高阶导数与 相关变化率 2.4 函数的微分 2.5 洛必达法则 2.6 微分中值定 理 2.7 泰勒公式 2.8 利用导数研 究函数的性态 2.9 平面曲线的 曲率 1、正确理解导数和微分的概念、 几何意义,熟悉函数可导性与连续 性的关系,会用导数和微分的定义 求简单函数的导数和微分。 2、掌握导数的四则运算法则、复 合函数和反函数的求导法则,熟练 掌握基本初等函数的导数及微分 公式;掌握微分的四则运算法则, 了解一阶微分形式不变性;会用求 导法则和求导公式计算初等函数 的导数或微分。 3、正确理解高阶导数的概念;会 求函数的二阶、三阶导数和一些较 简单函数的 n 阶导数。 4、会求隐函数和由参数方程所确 定的函数的导数和高阶导数。 5、正确理解罗尔定理、拉格朗日 中值定理、柯西中值定理和泰勒中 值定理,并会应用中值定理求解或 证明简单的中值问题。 6、正确理解函数极值的概念和判 别条件;掌握用导数判断函数的单 调性和求极值的方法;会判断函数 的单调性,会求函数的极值。 7、会用导数判断函数图形的凹凸 性;会求拐点;了解描绘函数的图 形的方法(包括水平和铅直渐近 线);会求解较简单的最大值和最 小值的应用问题。 8、正确理解罗必达法则,会用罗 必达法则求不定式的极限。 9、了解曲线的曲率和曲率半径的 概念,并会计算函数曲线的曲率和 曲率半径。 30 理论教 学 26 学时, 习题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 第三章 一元函 数积分 学及其 应用 3.1 定积分的概 念和性质 3.2 微积分基本 定理 3.3 不定积分 3.4 定积分的计 算 3.5 定积分应用 1、正确理解不定积分的概念及性 质。 2、掌握不定积分的基本积分公式; 会用换元积分法和分部积分法计 算不定积分;了解有理函数的积分 方法,会计算简单有理函数的不定 积分。 3、正确理解定积分的概念及性质; 32 理论教 学 28 学时, 习题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3

举例 孰暴疫明定积分函数 6广义积分 掌握定积分的基本积分公式 微积分基本定理和牛顿莱布尼 公式:会用换元积分法和分部积 法计算定积分。 了解无穷区间上的广义积分 无界函数广义积分的概念:会计算 较简单的广义积分。 6、会用定积分表达并计算一些钗 简单的几何量与物理量(如面积 体积、弧长、功、引力等)方法 、正确理解常微分方程的阶、解 通解、初始条件和特解等概念 2、掌握变量可分离微分方程及 阶线性微分方程的解法。 3、会解齐次方程、伯努力方程无 全微分方程:了解用变量代换求 4.1微分方程白 微分方程的基本思想方法。 甚本概今 4、会用降阶法求解下列微分方程 中较简单的方程: 在理企 42某些简单君 理论数 第四 分方程的初等积 y=f(.y) 学12 学习的 基础」 常微分 分法 学时 1、2、3 4.3建立微分 掌握二阶线性微分方程解的 完成调 方程 习顾调 构:会求解二阶常系数齐次线性很 后作 程方法简介 4.4高阶线性 分方程:了解高阶常系数齐次线性 2学时 业 微分方程 微分方程的解法 会求自由项形如: e[p,(x)cosox 7、会用微分方程解一些简单的几 何和物理问题。 合计 90 29
29 举例 3.6 广义积分 熟悉変限定积分函数。 4、掌握定积分的基本积分公式、 微积分基本定理和牛顿莱布尼茨 公式;会用换元积分法和分部积分 法计算定积分。 5、了解无穷区间上的广义积分和 无界函数广义积分的概念;会计算 较简单的广义积分。 6、会用定积分表达并计算一些较 简单的几何量与物理量(如面积、 体积、弧长、功、引力等)方法。 第四章 常微分 方程 4.1 微分方程的 基本概念 4.2 某些简单微 分方程的初等积 分法 4.3 建立微分方 程方法简介 4.4 高阶线性 微分方程 1、正确理解常微分方程的阶、解、 通解、初始条件和特解等概念。 2、掌握变量可分离微分方程及一 阶线性微分方程的解法。 3、会解齐次方程、伯努力方程和 全微分方程;了解用变量代换求解 微分方程的基本思想方法。 4、会用降阶法求解下列微分方程 中较简单的方程: ( ) ( ) n y fx = , y f xy ′′ ′ = (, ) 和 y f yy ′′ ′ = (, )。 5、掌握二阶线性微分方程解的结 构;会求解二阶常系数齐次线性微 分方程;了解高阶常系数齐次线性 微分方程的解法。 6 、会求自由项形如: x eλ , [ ( )cos x l e px x λ ω ( ) + p x n ⋅sin ] ωx 的二阶常系数非齐次线性 微分方程的特解与通解。 7、会用微分方程解一些简单的几 何和物理问题。 14 理论教 学 12 学时, 习题课 2 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 合 计 90 --
《高等数学B》教学大纲 (Advanced Mathematics B) ,基本信息 课程 B1420246(高等数学B1) 课程 编号 必修■选修口 B1420239(高等数学B2) 屈性 学分 9 总学时 理论 144 上机 0 实验 0 (6+3) (96+48) 学时 学时 学时 课程 公共基础■综合素质口大类基础口院内平台口专业基础口 类别 专业主干口 专业方向/特色口 专业任选口 顶峰课程口 先修 课程 开课 金融学、国际经济与留易、工商管理 信息工程学院 适用 专业 市场营销、会计学、旅游管理、酒店管理 课程负 刘自新 撰写人 刘自新 审核人 则家泰 责人 二、课程说明 1课程介绍 高等数学B是高等学校工管类、旅游类各专业必修的一门公共基础课。本 课程包括的主要内容有:一元函数的极限、连续、微积分及其应用:无穷级数、 空间解析几何、多元函数的极限、连续、微积分及其应用,常微分方程。通过本 课程的教学,使学生系统地掌握函数的极限、连续、微积分、无穷级数、空间解 析几何方面的基本概念、基本理论和基本方法,培养学生抽象概括能力、逻辑推 理能力、空间想象能力、综合分析能力以及运用所学知识解决实际问题的能力, 为后继课程的学习和将来从事科研和其它实际工作奠定必要的数学基础。 Advanced Mathematics B is an important public basic mathematics courses for all majors in engineering and tourism.The main contents of this course include:limit. continuity,calculus and its application of unary function;infinite series,spatial analytic geometry,limit,continuity,calculus and its application of multivariate function,ordinary differential equation.Through the teaching of this course,students can systematically master the basic concepts,basic theories and basic methods of the limit,continuity,calculus,infinite series and spatial analytic geometry,and cultivate studentsabstract generalization ability,logical reasoning ability,spatial imagination. comprehensive analytical ability,and the ability to apply what they have learned to solve practical problems,provide the necessary mathematical foundation for the study of subsequent courses and future research and other practical work 2.课程目标 目标1(知识目标):通过本课程的教学,使学生能够正确理解微积分的基
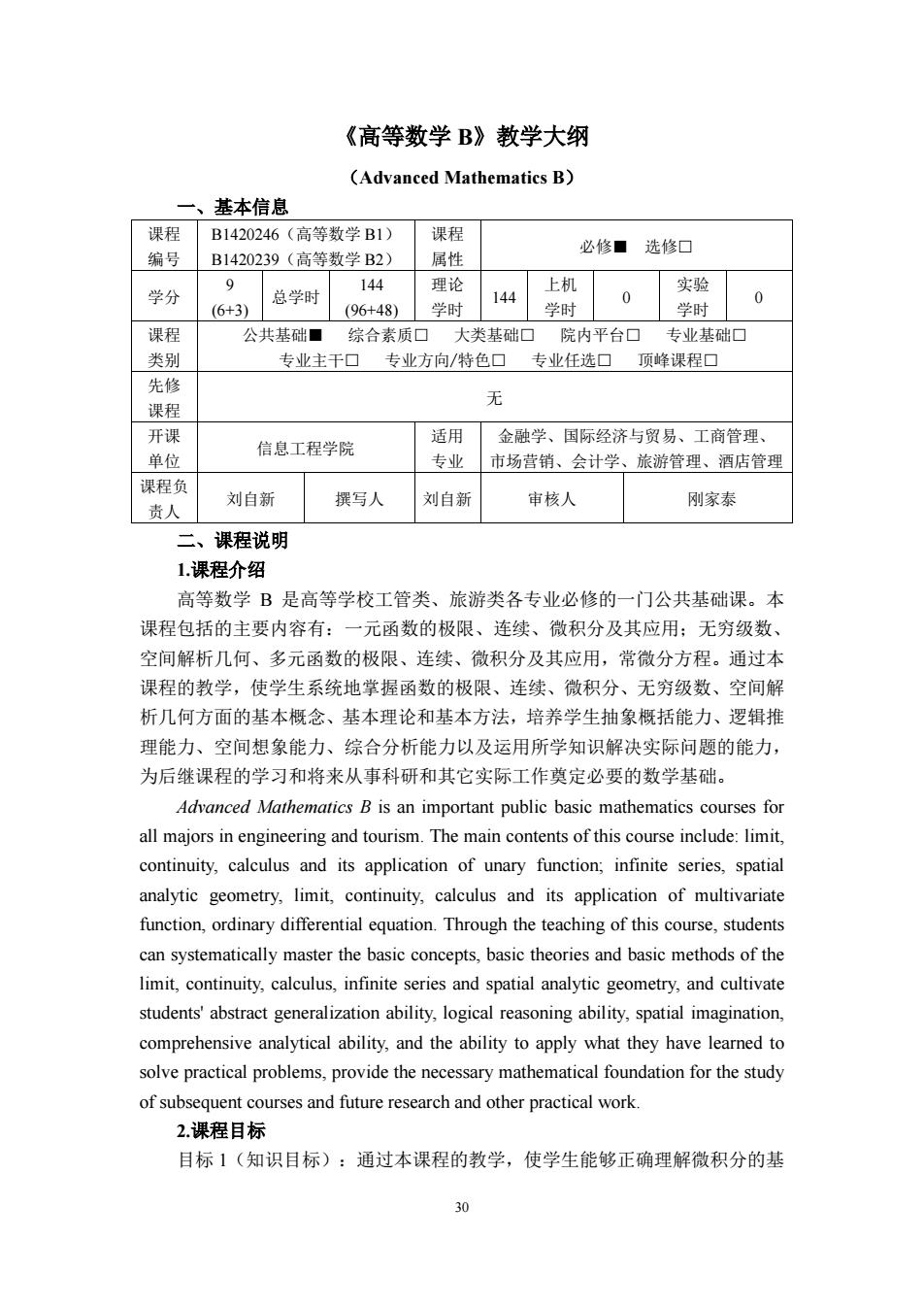
30 《高等数学 B》教学大纲 (Advanced Mathematics B) 一、基本信息 课程 编号 B1420246(高等数学 B1) B1420239(高等数学 B2) 课程 属性 必修■ 选修□ 学分 9 (6+3) 总学时 144 (96+48) 理论 学时 144 上机 学时 0 实验 学时 0 课程 类别 公共基础■ 综合素质□ 大类基础□ 院内平台□ 专业基础□ 专业主干□ 专业方向/特色□ 专业任选□ 顶峰课程□ 先修 课程 无 开课 单位 信息工程学院 适用 专业 金融学、国际经济与贸易、工商管理、 市场营销、会计学、旅游管理、酒店管理 课程负 责人 刘自新 撰写人 刘自新 审核人 刚家泰 二、课程说明 1.课程介绍 高等数学 B 是高等学校工管类、旅游类各专业必修的一门公共基础课。本 课程包括的主要内容有:一元函数的极限、连续、微积分及其应用;无穷级数、 空间解析几何、多元函数的极限、连续、微积分及其应用,常微分方程。通过本 课程的教学,使学生系统地掌握函数的极限、连续、微积分、无穷级数、空间解 析几何方面的基本概念、基本理论和基本方法,培养学生抽象概括能力、逻辑推 理能力、空间想象能力、综合分析能力以及运用所学知识解决实际问题的能力, 为后继课程的学习和将来从事科研和其它实际工作奠定必要的数学基础。 Advanced Mathematics B is an important public basic mathematics courses for all majors in engineering and tourism. The main contents of this course include: limit, continuity, calculus and its application of unary function; infinite series, spatial analytic geometry, limit, continuity, calculus and its application of multivariate function, ordinary differential equation. Through the teaching of this course, students can systematically master the basic concepts, basic theories and basic methods of the limit, continuity, calculus, infinite series and spatial analytic geometry, and cultivate students' abstract generalization ability, logical reasoning ability, spatial imagination, comprehensive analytical ability, and the ability to apply what they have learned to solve practical problems, provide the necessary mathematical foundation for the study of subsequent courses and future research and other practical work. 2.课程目标 目标 1(知识目标):通过本课程的教学,使学生能够正确理解微积分的基
本概念和基本理论,掌握微积分运算的基本方法,了解微积分在几何和经济上的 应用。 目标2(能力目标):通过本课程的教学,使学生具备科学研究中初步的微 积分的运算求解能力,培养学生的推理论证能力、抽象概括能力和运用数学技巧 简化数学运算的能力。 目标3(素质目标):通过本课程的教学,培养学生的数学思维能力和严谨 求实的科学态度,提高学生的数学素养,能够利用微分解决本专业中简单的实际 应用问题。 3.课程资源 (1)推荐参考教材及参考书目 类别 教材名称 主编 出版社 出版时间 参老教材 微积分 在域树顺 中国人民大学出版社2018.5 微积分 阁慧臻 大连理工大学出版社 2014.8 微积分及其应用 拉里J戈德斯坦等 中国人民大学出版社 2019.6 参考书目 微积分(第四版 赵树短胡显佑陆启 学习参考 良楮水增 中国人民大学出版社 2018.7 (2)课程网站 微积分基础北京大学_中国大学MOOC(慕课) https://www.icourse163.org/course/PKU-1002530002 高等数学(一)同济大学中国大学M0OC(慕课) https://www.icoursel63.org/course/TONGJI-53004 高等数学(二)_同济大学_中国大学MO0C(慕课 https://www.icoursel63.org/course/TONGJI-217012 高等数学(三)_同济大学_中国大学MOOC(慕课) https://www.icourse163.org/course/TONGJI-284001 高等数学(四)同济大学中国大学MOOC(慕课) https://www.icoursel63.org/course/TONGJI-1001569002 4.考核及成绩评价标准 考核方式:考试 评价标淮 高等数学B】 成绩构成 评价方式 评价依据 课后作业 主要考核学生对每章节知识点的复习、理解和掌握程 度,每次作业单独评分,每周检查作业1次,占平时 平时成绩 成绩60% (20%) 课堂交流 主要考核学生对所学知识的理解能力及应用所学知识 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩20%。 31
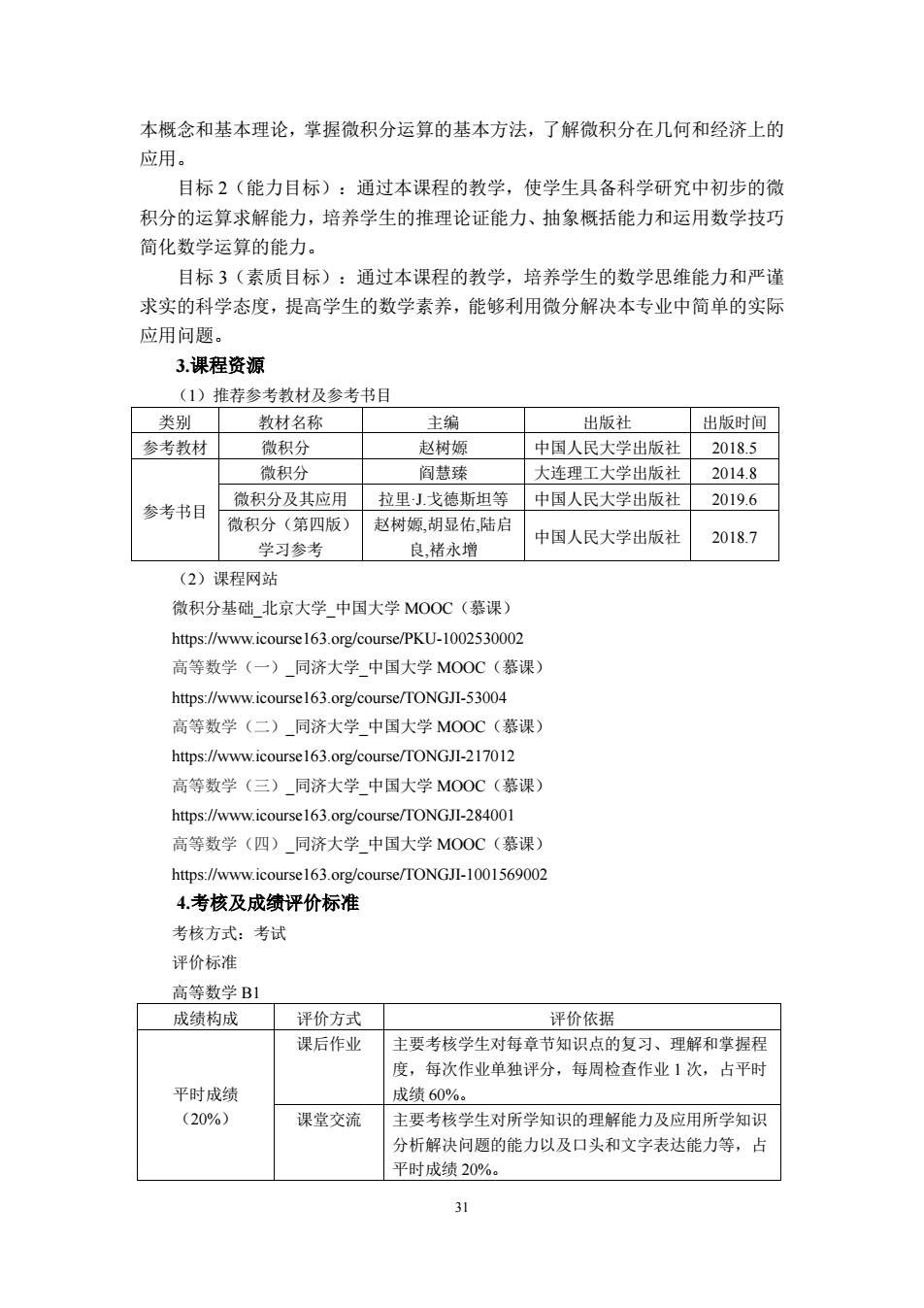
31 本概念和基本理论,掌握微积分运算的基本方法,了解微积分在几何和经济上的 应用。 目标 2(能力目标):通过本课程的教学,使学生具备科学研究中初步的微 积分的运算求解能力,培养学生的推理论证能力、抽象概括能力和运用数学技巧 简化数学运算的能力。 目标 3(素质目标):通过本课程的教学,培养学生的数学思维能力和严谨 求实的科学态度,提高学生的数学素养,能够利用微分解决本专业中简单的实际 应用问题。 3.课程资源 (1)推荐参考教材及参考书目 类别 教材名称 主编 出版社 出版时间 参考教材 微积分 赵树嫄 中国人民大学出版社 2018.5 参考书目 微积分 阎慧臻 大连理工大学出版社 2014.8 微积分及其应用 拉里·J.戈德斯坦等 中国人民大学出版社 2019.6 微积分(第四版) 学习参考 赵树嫄,胡显佑,陆启 良,褚永增 中国人民大学出版社 2018.7 (2)课程网站 微积分基础_北京大学_中国大学 MOOC(慕课) https://www.icourse163.org/course/PKU-1002530002 高等数学(一)_同济大学_中国大学 MOOC(慕课) https://www.icourse163.org/course/TONGJI-53004 高等数学(二)_同济大学_中国大学 MOOC(慕课) https://www.icourse163.org/course/TONGJI-217012 高等数学(三)_同济大学_中国大学 MOOC(慕课) https://www.icourse163.org/course/TONGJI-284001 高等数学(四)_同济大学_中国大学 MOOC(慕课) https://www.icourse163.org/course/TONGJI-1001569002 4.考核及成绩评价标准 考核方式:考试 评价标准 高等数学 B1 成绩构成 评价方式 评价依据 平时成绩 (20%) 课后作业 主要考核学生对每章节知识点的复习、理解和掌握程 度,每次作业单独评分,每周检查作业 1 次,占平时 成绩 60%。 课堂交流 主要考核学生对所学知识的理解能力及应用所学知识 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩 20%