出勤及随机 主要考核学生出勤情况及对当堂课程的接受能力,占 测验 平时成绩20%。 期末考试 闭卷考试 主要题型有填空题、选择题、计算题和综合题等。其 (80%) 中,基础知识题约占70%,能力题约占30%。 高等数学B2 成绩构成 评价方式 评价依据 主要考核学生对每章节知识点的复习、理解和掌握程 课后作业 度,每次作业单独评分,每周检查作业1次,占平时 成结60%。 平时成结 主要考核学生对所学知识的理解能力及应用所学知识 (30% 课堂交流 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩20% 出勤及随机 主要考核学生出勒情况及对当堂课程的接受能力,占 测验 平时成绩20% 期末考试 闭卷考试 主要题型有填空题、选择题、计算题和综合题等。其 (70%) 中,基础知识题约占70%,能力题约占30%。 三、教学内容及要求 高等数学B1 教学 对应的 章节 主要内容 教学要求 学时方法和手段 课程 课内课后目标 1集合 12实数集 通过对本章内容的教学, 3函数关系 生能铭掌握函数的奇偶性、宝 14分段函数 5建立函数关系 调性、围期性和有界性 。能 列题 理解复合函数及分段函数的 复习初 了解反函数及隐函数的相 第一章 16函数的几种简单 理论 等数学 函数 教学 的有关 2 2能够堂郴基木初等函数的松 1.7反函数与复合 质及其图形。理解初等函数 知识 函数 概念 1.8初等函数 3会建立简单应用问题中的 9函数图形的简单 数关系式 组合与变换 21数列的极限 通过本章内容的教学,学生 在理诊 2.2函数的极阳 能够理解极限的概念,理解 理论教 学习的 2.3变量的极 数左极限与右极限的概念 14学 极限 4无穷大量与无 及极限存在与左、右极限之 16 时 基础」 2、 连续 穷小量 的关系。 题 完成溪 后作 2.5极限的运算法则2.能够掌握极限的性质及四则 学时 2.6两个重要的极限运算法则。掌握极限存在的两
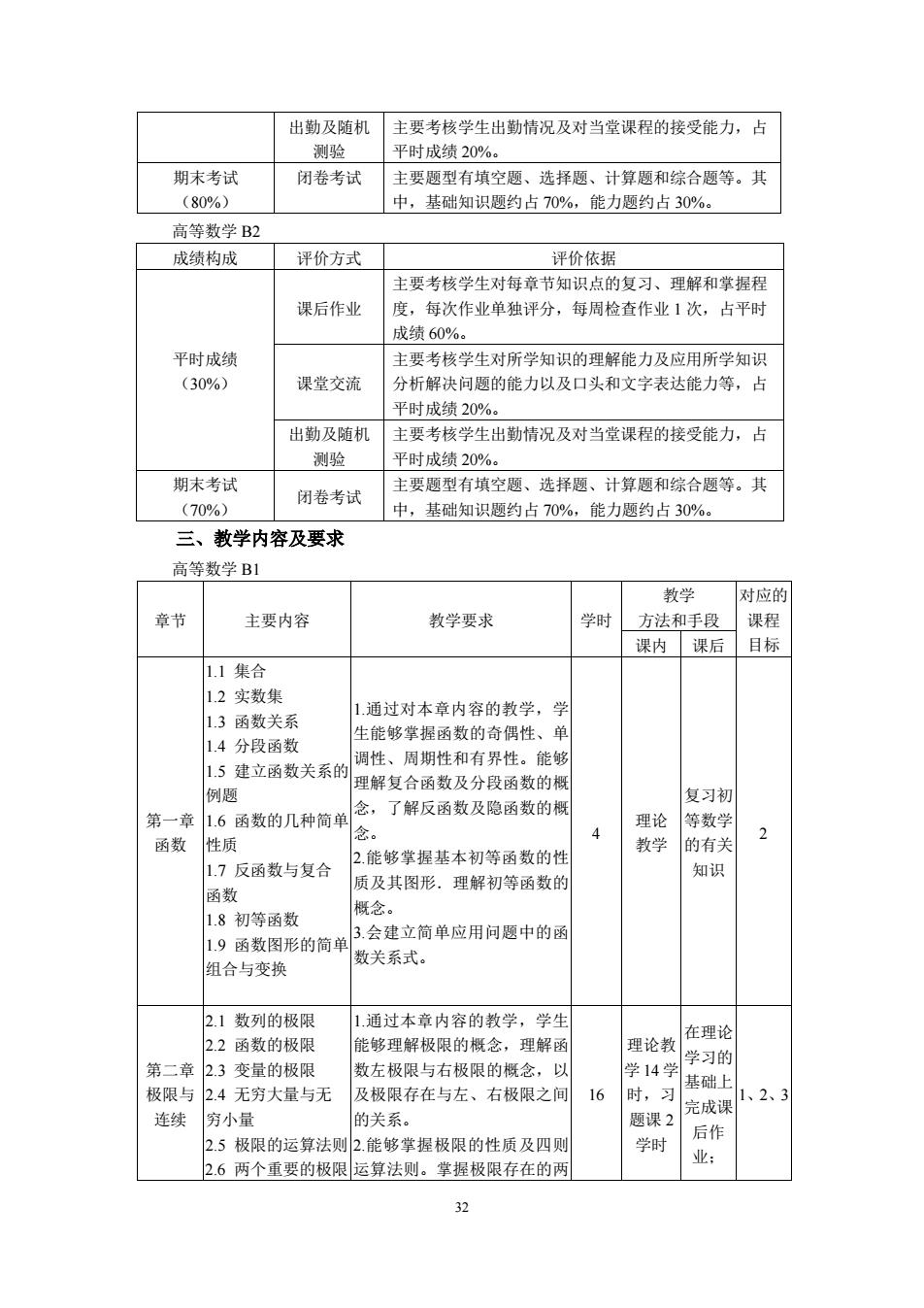
32 出勤及随机 测验 主要考核学生出勤情况及对当堂课程的接受能力,占 平时成绩 20%。 期末考试 (80%) 闭卷考试 主要题型有填空题、选择题、计算题和综合题等。其 中,基础知识题约占 70%,能力题约占 30%。 高等数学 B2 成绩构成 评价方式 评价依据 平时成绩 (30%) 课后作业 主要考核学生对每章节知识点的复习、理解和掌握程 度,每次作业单独评分,每周检查作业 1 次,占平时 成绩 60%。 课堂交流 主要考核学生对所学知识的理解能力及应用所学知识 分析解决问题的能力以及口头和文字表达能力等,占 平时成绩 20%。 出勤及随机 测验 主要考核学生出勤情况及对当堂课程的接受能力,占 平时成绩 20%。 期末考试 (70%) 闭卷考试 主要题型有填空题、选择题、计算题和综合题等。其 中,基础知识题约占 70%,能力题约占 30%。 三、教学内容及要求 高等数学 B1 章节 主要内容 教学要求 学时 教学 方法和手段 对应的 课程 课内 课后 目标 第一章 函数 1.1 集合 1.2 实数集 1.3 函数关系 1.4 分段函数 1.5 建立函数关系的 例题 1.6 函数的几种简单 性质 1.7 反函数与复合 函数 1.8 初等函数 1.9 函数图形的简单 组合与变换 1.通过对本章内容的教学,学 生能够掌握函数的奇偶性、单 调性、周期性和有界性。能够 理解复合函数及分段函数的概 念,了解反函数及隐函数的概 念。 2.能够掌握基本初等函数的性 质及其图形.理解初等函数的 概念。 3.会建立简单应用问题中的函 数关系式。 4 理论 教学 复习初 等数学 的有关 知识 2 第二章 极限与 连续 2.1 数列的极限 2.2 函数的极限 2.3 变量的极限 2.4 无穷大量与无 穷小量 2.5 极限的运算法则 2.6 两个重要的极限 1.通过本章内容的教学,学生 能够理解极限的概念,理解函 数左极限与右极限的概念,以 及极限存在与左、右极限之间 的关系。 2.能够掌握极限的性质及四则 运算法则。掌握极限存在的两 16 理论教 学 14 学 时,习 题课 2 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3
2.7利用等价无穷小个法则,并会利用它们求极限 量代换求极限 会利用两个重要极限求极限 8函数的连续性 3.能够理解无穷小、无穷大日 概念,堂握无穷小阶的比较 法,会用箅价无穷小求极限 4能够理解函数连续性的概 (含左连续与右连续的概念, 判别函数间断点的类型和讨论 函数的连续性。 5.了解连续函数的性质和初等 函数的连续性,了解闭区间 连续函数的性质(有界性、最大 值、最小值定理和介值定理)及 其简单的应用。 1.通过本章的教学,学生能 理解导数和微分的概念,理 导数与微分的关系,理解导智 的几何意义,会求平面曲线自 切线方程,了解导数的经济 义,理解函数的可导性与连续 性之间的关系。 3.1引出导数概念 会用基本初等函数的导数 导数的四则运算法则和 伤例题 合函数的求导法则求函数的导 理论毂 在理论 32导数的概今 学习的 第三章 新 学16兰 33导数的基本公 基础上 导数上 能铭了螺微分的四则运算 与运算法则 20 时,习 元成课 1、2、 微分 3.4高阶导数 则和 阶微分形式的不变性 后作 了解微分 学时 3.5微分 会求函数的微分, 业: 近似计算中的应用。 4.了解高阶导数的概念 会 简单函数的高阶导数 5.会求分段函数的一阶、二 导数。 6会求隐函数的一阶 、二阶号 数 会求反函数的导数 7.会求由参数方程确定的函药 的导数。 41中值定理 1能铭理解罗尔定理和拉格 在理论 第四 42洛必达法则 理论载 中 日中值定理的条件和结论, 学习的 4.3函数的增减性 握其简单的应用。 理与导 18 时, 习 基础上 1、2、3 4.4函数的极值 2.能够了解并会用柯西中值定 完成课 数的应 题课 45最大值与最小 理 用 后作 值,极值的应用问题 3.会用洛必达法则求未定式极 学时 33
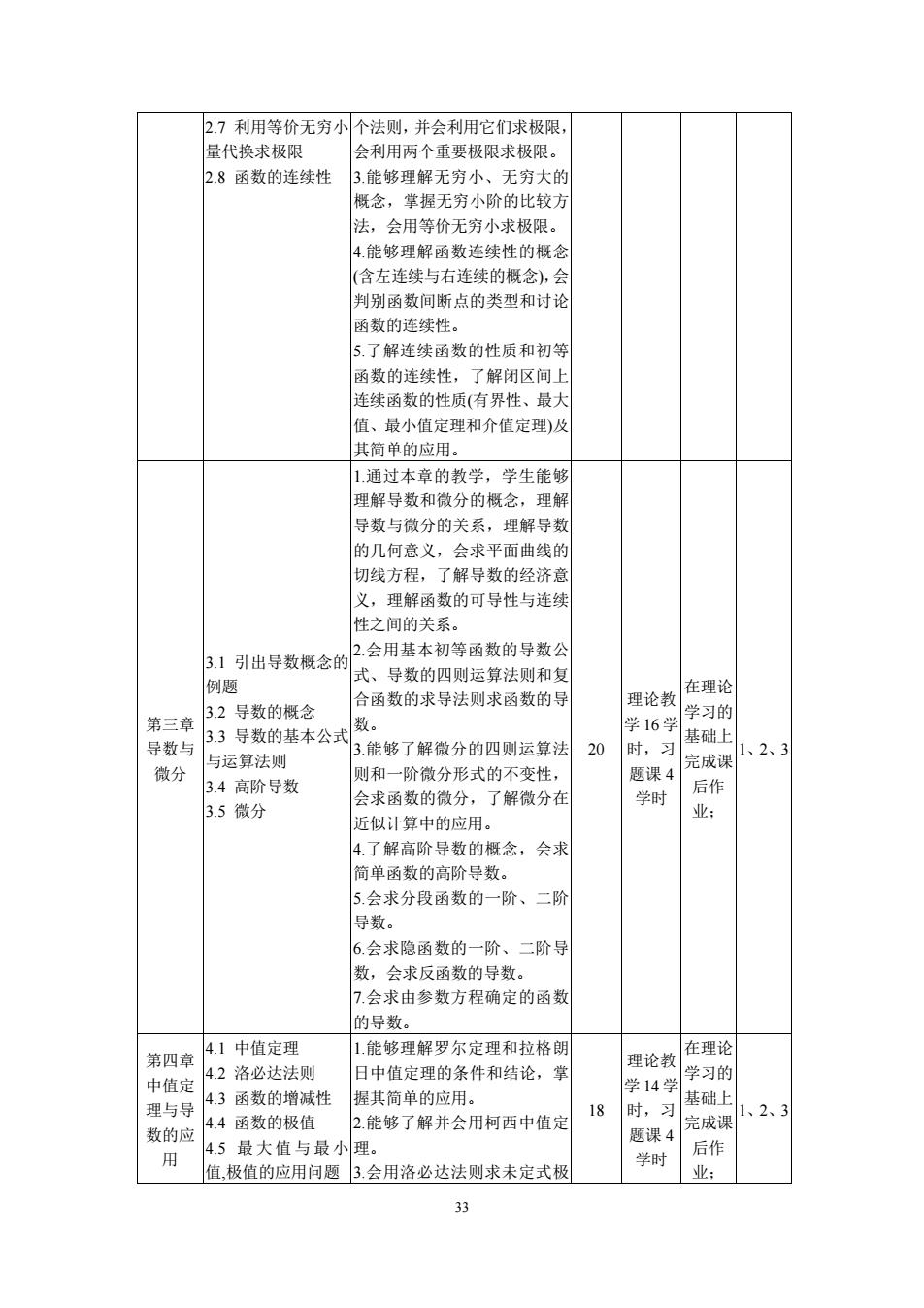
33 2.7 利用等价无穷小 量代换求极限 2.8 函数的连续性 个法则,并会利用它们求极限, 会利用两个重要极限求极限。 3.能够理解无穷小、无穷大的 概念,掌握无穷小阶的比较方 法,会用等价无穷小求极限。 4.能够理解函数连续性的概念 (含左连续与右连续的概念),会 判别函数间断点的类型和讨论 函数的连续性。 5.了解连续函数的性质和初等 函数的连续性,了解闭区间上 连续函数的性质(有界性、最大 值、最小值定理和介值定理)及 其简单的应用。 第三章 导数与 微分 3.1 引出导数概念的 例题 3.2 导数的概念 3.3 导数的基本公式 与运算法则 3.4 高阶导数 3.5 微分 1.通过本章的教学,学生能够 理解导数和微分的概念,理解 导数与微分的关系,理解导数 的几何意义,会求平面曲线的 切线方程,了解导数的经济意 义,理解函数的可导性与连续 性之间的关系。 2.会用基本初等函数的导数公 式、导数的四则运算法则和复 合函数的求导法则求函数的导 数。 3.能够了解微分的四则运算法 则和一阶微分形式的不变性, 会求函数的微分,了解微分在 近似计算中的应用。 4.了解高阶导数的概念,会求 简单函数的高阶导数。 5.会求分段函数的一阶、二阶 导数。 6.会求隐函数的一阶、二阶导 数,会求反函数的导数。 7.会求由参数方程确定的函数 的导数。 20 理论教 学 16 学 时,习 题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 第四章 中值定 理与导 数的应 用 4.1 中值定理 4.2 洛必达法则 4.3 函数的增减性 4.4 函数的极值 4.5 最大值与最小 值,极值的应用问题 1.能够理解罗尔定理和拉格朗 日中值定理的条件和结论,掌 握其简单的应用。 2.能够了解并会用柯西中值定 理。 3.会用洛必达法则求未定式极 18 理论教 学 14 学 时,习 题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3
4.6曲线的凹向与 拐点 .能够理解函数的极值概念 47函数图形的作法 会用导数判断函数的单调性不 4.8变化率及相对变求函数极值的方法,会求闭区 化率在经济中的应间上连缝函数的是大情和是 用 边际分析与弹 性分析介绍 5.会用导数判断函数图形的日 向和拐点,会求函数图形的水 平、铅直和斜渐诉线,会描么 某些简单函数的图形。 1,能够理解原函数概念和不月 5.1不定积分的概今 积分概念。 在理论 52不定积分的性厨 理论教 2堂握不定积分的基本性质 第五章 5.3基本积分公式 不定积分的基本公式, 4 学习的 不定 5.4换元积分法 时, 基础 1、2、3 3,用换元积分法与分部积分 完成误 分 5.5分部积分法 求不定积分。 题课4 后作 5.6综合杂例 学时 4合求简单的有理函数的 1能够理解定积分的概念和挂 61引出定积分概多 本性质,了解积分中值定理。 的例 2合求变上限定积分定义的 :定积分的定义 数的求导 掌握牛顿一莱布厅 3定积分的基本性茨公式。 3.会用换元积分法与分部积分 在理论 理论教 4微积分基本定理法求定积分 学习的 第六 定积分的换元 理解广义积分的概念并会 16学 时 基础」 1、2、3 定积分 分法 算广义积分,了解厂函数的和 6.6定积分的分部积 课4 完成课 分 学时 后作 分法 了解定积分的近似计算法 6.7定积分的应用 6.会用定积分计算 些几何 6.8广义积分与1 (平面图形的面积、旋转体 函数 体积)。 门会用积分学原理解决一些 济方面应用题, 合计 96
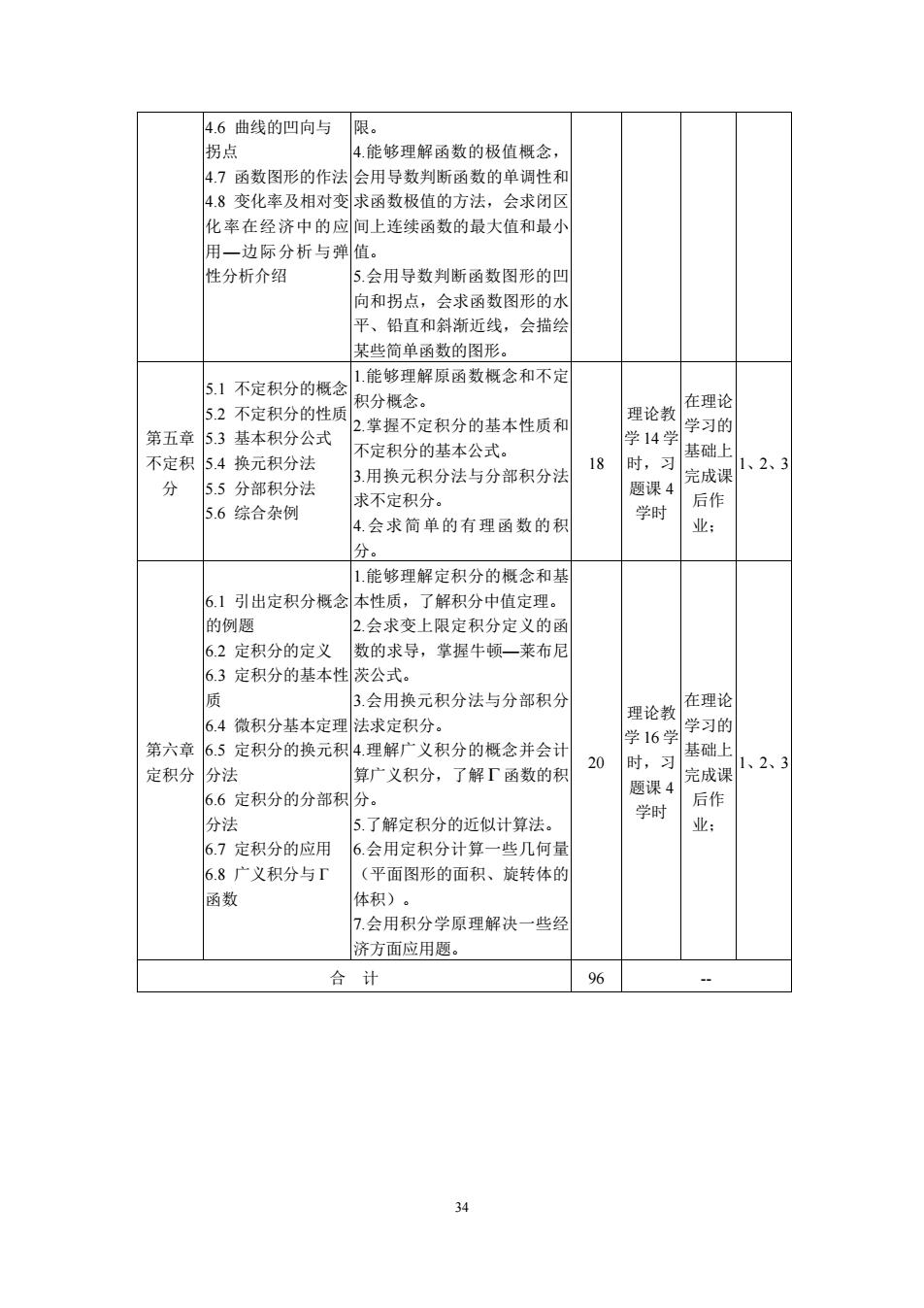
34 4.6 曲线的凹向与 拐点 4.7 函数图形的作法 4.8 变化率及相对变 化率在经济中的应 用—边际分析与弹 性分析介绍 限。 4.能够理解函数的极值概念, 会用导数判断函数的单调性和 求函数极值的方法,会求闭区 间上连续函数的最大值和最小 值。 5.会用导数判断函数图形的凹 向和拐点,会求函数图形的水 平、铅直和斜渐近线,会描绘 某些简单函数的图形。 第五章 不定积 分 5.1 不定积分的概念 5.2 不定积分的性质 5.3 基本积分公式 5.4 换元积分法 5.5 分部积分法 5.6 综合杂例 1.能够理解原函数概念和不定 积分概念。 2.掌握不定积分的基本性质和 不定积分的基本公式。 3.用换元积分法与分部积分法 求不定积分。 4.会求简单的有理函数的积 分。 18 理论教 学 14 学 时,习 题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 第六章 定积分 6.1 引出定积分概念 的例题 6.2 定积分的定义 6.3 定积分的基本性 质 6.4 微积分基本定理 6.5 定积分的换元积 分法 6.6 定积分的分部积 分法 6.7 定积分的应用 6.8 广义积分与 Γ 函数 1.能够理解定积分的概念和基 本性质,了解积分中值定理。 2.会求变上限定积分定义的函 数的求导,掌握牛顿—莱布尼 茨公式。 3.会用换元积分法与分部积分 法求定积分。 4.理解广义积分的概念并会计 算广义积分,了解 Γ 函数的积 分。 5.了解定积分的近似计算法。 6.会用定积分计算一些几何量 (平面图形的面积、旋转体的 体积)。 7.会用积分学原理解决一些经 济方面应用题。 20 理论教 学 16 学 时,习 题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 合 计 96 --
高等数学B2 教学 对应的 章节 主要内容 教学要求 学时方法和手段 课程 课内课后 目标 通过对常数项级数收敛、发散 及收敛级数的和的概念以及级数 基本性质的学习,学生能判断简年 吸数的敛散性 2通过对正项级数的比较判别法 7.1无穷级数的 概念 比值判别法、根值判法学习,学生 能根据常见的几何级数与P级数 基本性质 收敛与发散的条件,判断正项级 的敛散性。 73正项级数 3.能根据莱布尼茨定理判断交错级 7.4任意项级数 阻诊教 复习初 数的敛散性。 绝对收敛 等数量 第七章 75幂级数 4能根据相关定理判断任意项级菱 学16 的有关 无穷 的绝对收敛与条件收敛 1、2、3 7.6勒公式 学时 知识, 数 泰勒级数 5.会求幂级数的收敛半径、收敛区 习题谋 完成舆 间和收敛域。 2学时 7.7某些初等 后作业 的幂级数展 了解幂级数在其收敛区间内的 些基本性质,会求一些幂级数在此 78系级数的下 敛区间内的和函数,并会由此求出 某些数项级数的和。 用举例 了解泰勒中值定理及泰勒级数 能够利用e 、s1nx、和(1+x) 的麦克劳林展开式,将一些简单医 数间接展开成幂级数。 9.了解幂级数在近似计算上的简 立用。 8.I空间解析几1能够理解二元函数的几何意义, 何简介 了解二元函数的极限与连续性 82多元函数的概念 概念 2.会求多元函数的偏导数 二阶1 83二元函数的导数和全微分,了解全微分在近化 在理论 理论教 极阻与连续 计算中的应用。 学习的 第八章 学16 多元函 8.4偏导数与全3.会求多元复合函数的偏导数及附 基础上 函数的偏导数 20 、2、 8.5复合函数日 4.理解二元函数极值和条件极值 后作 4学时 微分法与隐函数概念,掌握二元函数极值存在的心 业 的微分法 要条件,了解一元函数极值存在 6 二元函数 充分条件 会求 元函数的极值 设值 会用拉格朗日乘数法求条件极值 8.7二重积分 会求简单多元函数的最大值和最 35
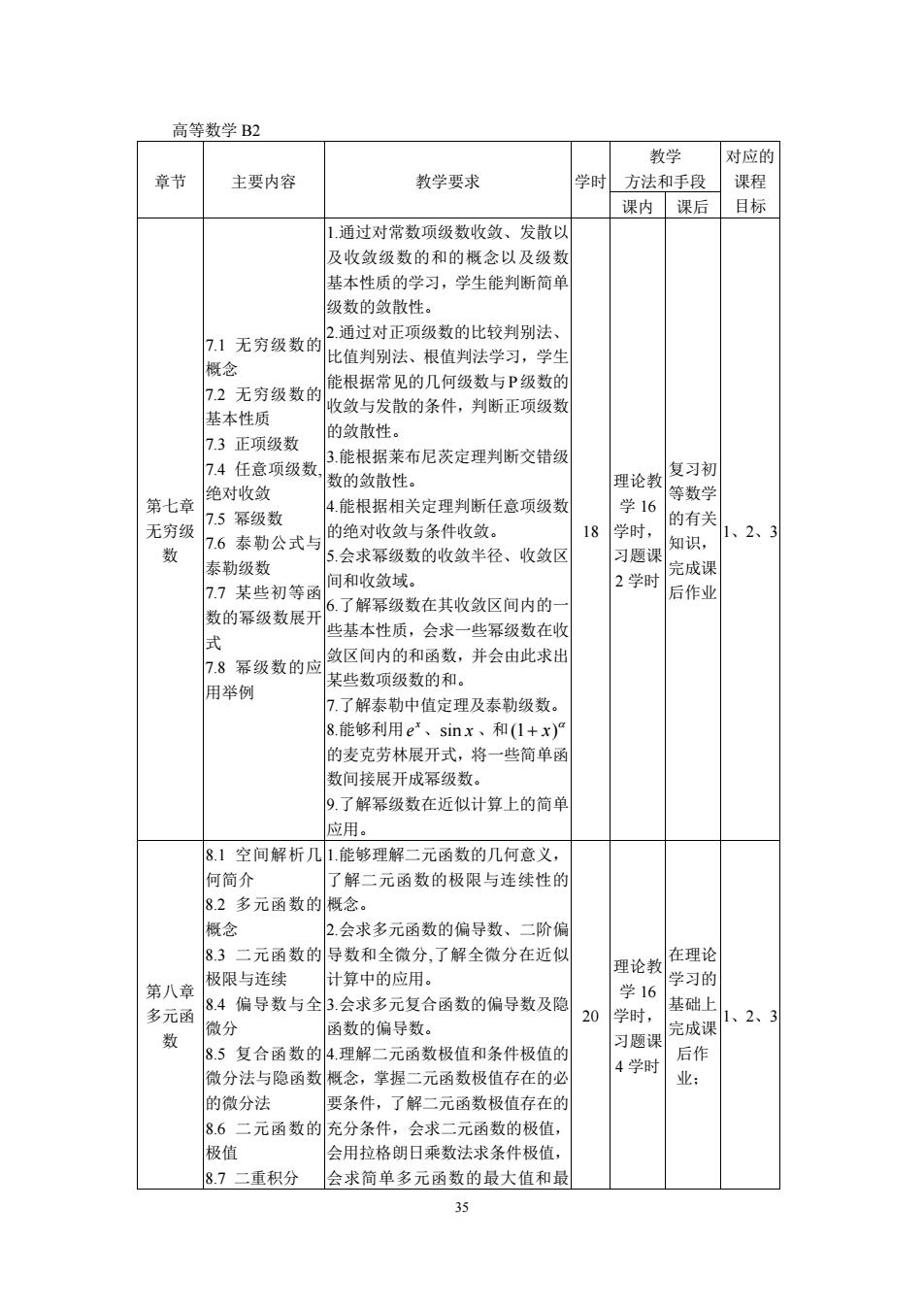
35 高等数学 B2 章节 主要内容 教学要求 学时 教学 方法和手段 对应的 课程 课内 课后 目标 第七章 无穷级 数 7.1 无穷级数的 概念 7.2 无穷级数的 基本性质 7.3 正项级数 7.4 任意项级数, 绝对收敛 7.5 幂级数 7.6 泰勒公式与 泰勒级数 7.7 某些初等函 数的幂级数展开 式 7.8 幂级数的应 用举例 1.通过对常数项级数收敛、发散以 及收敛级数的和的概念以及级数 基本性质的学习,学生能判断简单 级数的敛散性。 2.通过对正项级数的比较判别法、 比值判别法、根值判法学习,学生 能根据常见的几何级数与P级数的 收敛与发散的条件,判断正项级数 的敛散性。 3.能根据莱布尼茨定理判断交错级 数的敛散性。 4.能根据相关定理判断任意项级数 的绝对收敛与条件收敛。 5.会求幂级数的收敛半径、收敛区 间和收敛域。 6.了解幂级数在其收敛区间内的一 些基本性质,会求一些幂级数在收 敛区间内的和函数,并会由此求出 某些数项级数的和。 7.了解泰勒中值定理及泰勒级数。 8.能够利用 x e 、sin x 、和(1 ) x α + 的麦克劳林展开式,将一些简单函 数间接展开成幂级数。 9.了解幂级数在近似计算上的简单 应用。 18 理论教 学 16 学时, 习题课 2 学时 复习初 等数学 的有关 知识, 完成课 后作业 1、2、3 第八章 多元函 数 8.1 空间解析几 何简介 8.2 多元函数的 概念 8.3 二元函数的 极限与连续 8.4 偏导数与全 微分 8.5 复合函数的 微分法与隐函数 的微分法 8.6 二元函数的 极值 8.7 二重积分 1.能够理解二元函数的几何意义, 了解二元函数的极限与连续性的 概念。 2.会求多元函数的偏导数、二阶偏 导数和全微分,了解全微分在近似 计算中的应用。 3.会求多元复合函数的偏导数及隐 函数的偏导数。 4.理解二元函数极值和条件极值的 概念,掌握二元函数极值存在的必 要条件,了解二元函数极值存在的 充分条件,会求二元函数的极值, 会用拉格朗日乘数法求条件极值, 会求简单多元函数的最大值和最 20 理论教 学 16 学时, 习题课 4 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3
小值,并会解决一些简单的应用问 5理解二重积分的概念,掌握二耳 积分的性质。会利用直角坐标和极 坐标计算二重积分 理解微分方程及其解、阶、 通解 初始条件和特解等概念。 9.1微分方程的2.会求解可分离变量方程、齐次方 船概令 程及一阶线性方程】 一阶微分方 会用降阶法解下列方程: 程 y=f(x),y"-fx,y)利 .3几种二阶微y=fy,y) 在理诊 理论教 分方程 学习的 第九章 4.会解二阶常系数齐次线性微分 二阶常系数程, 会用参数变异法求解 一些简单 基础」 常做分 10 1、2、3 线性微分方程 的二阶常系数非齐次线性微分方 完成误 方程 95差分方程 的程的特解和通解。 题课2 5.会用微分方程(或方程组)解决 学时 后作 一船概令 业 .6 些简单的应用问题 常系数线性差分 6.理解差分方程及其解、阶、通解 方程 初始条件和特解等概念。 7会解一阶和一阶常系数线性差 方程 合计 48 6
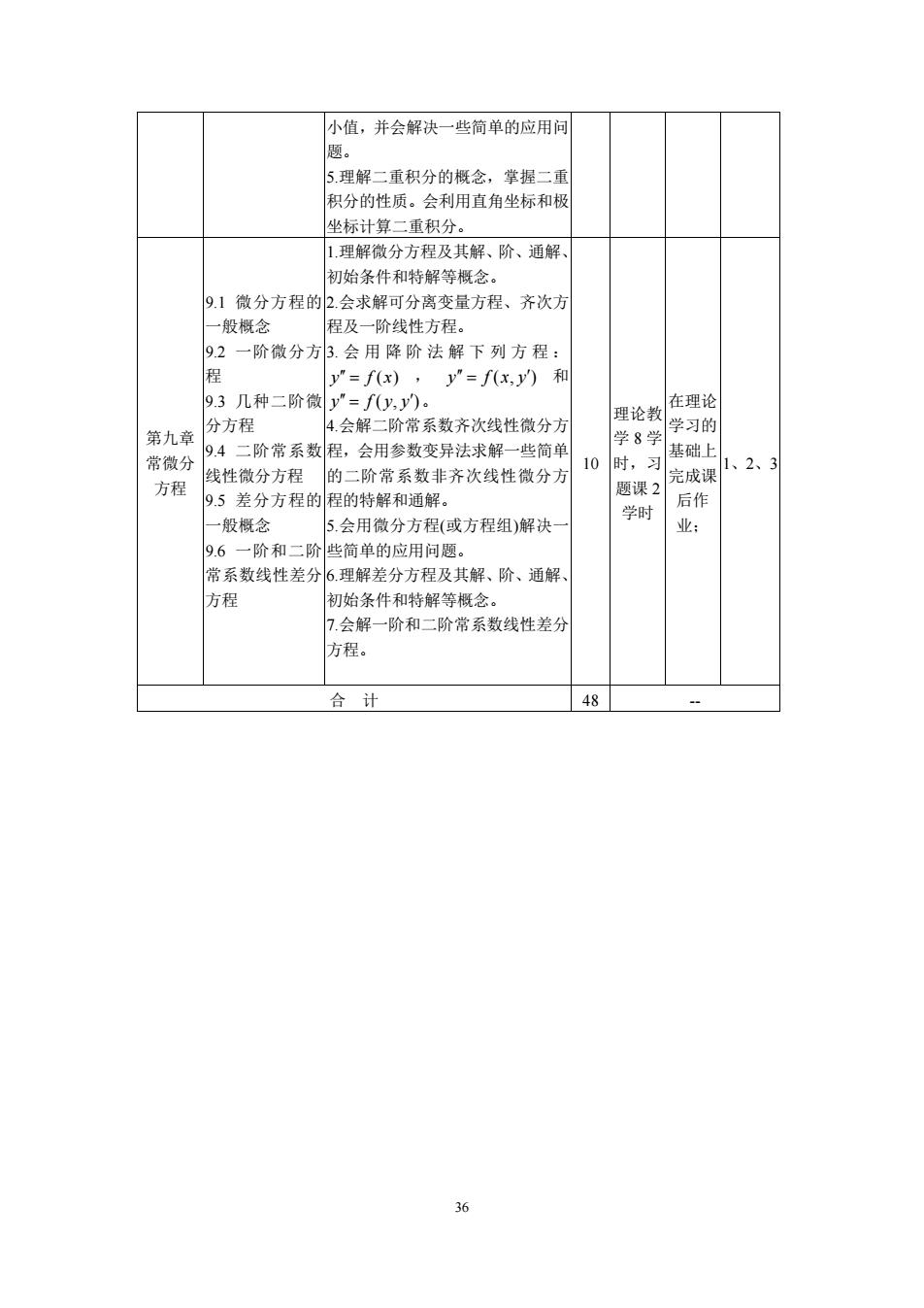
36 小值,并会解决一些简单的应用问 题。 5.理解二重积分的概念,掌握二重 积分的性质。会利用直角坐标和极 坐标计算二重积分。 第九章 常微分 方程 9.1 微分方程的 一般概念 9.2 一阶微分方 程 9.3 几种二阶微 分方程 9.4 二阶常系数 线性微分方程 9.5 差分方程的 一般概念 9.6 一阶和二阶 常系数线性差分 方程 1.理解微分方程及其解、阶、通解、 初始条件和特解等概念。 2.会求解可分离变量方程、齐次方 程及一阶线性方程。 3. 会用降阶法解下列方程: y fx ′′ = ( ) , y f xy ′′ ′ = (, ) 和 y f yy ′′ ′ = (, )。 4.会解二阶常系数齐次线性微分方 程,会用参数变异法求解一些简单 的二阶常系数非齐次线性微分方 程的特解和通解。 5.会用微分方程(或方程组)解决一 些简单的应用问题。 6.理解差分方程及其解、阶、通解、 初始条件和特解等概念。 7.会解一阶和二阶常系数线性差分 方程。 10 理论教 学 8 学 时,习 题课 2 学时 在理论 学习的 基础上 完成课 后作 业; 1、2、3 合 计 48 --