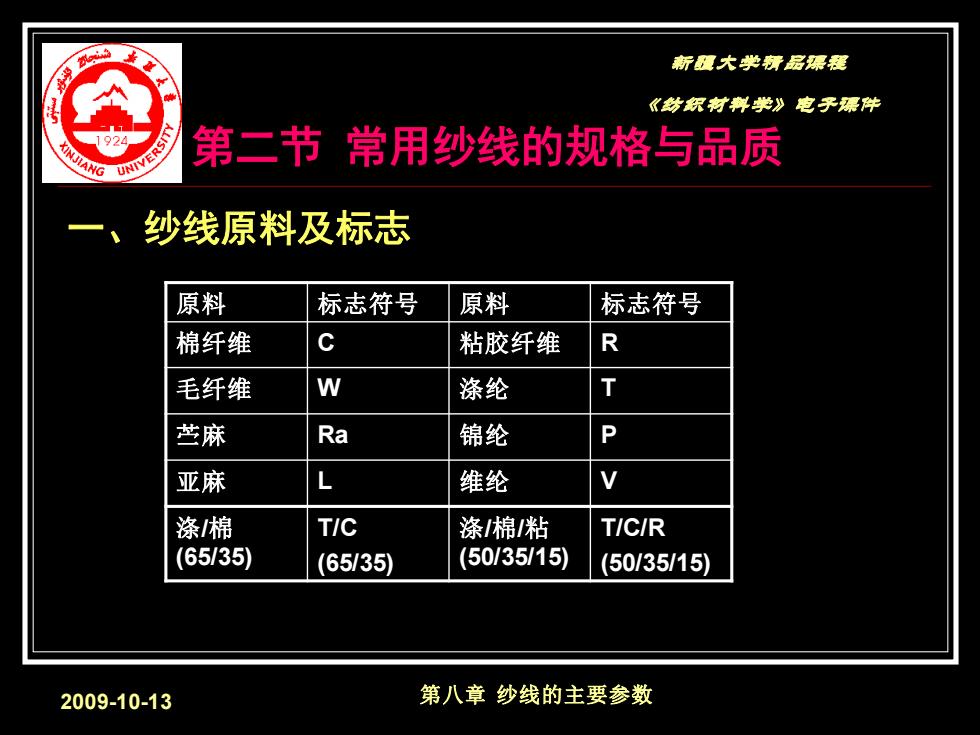
新程大学精品渠程 《梦织材料学》电子暴件 1924 第二节常用纱线的规格与品质 ANG 纱线原料及标志 原料 标志符号 原料 标志符号 棉纤维 c 粘胶纤维 R 毛纤维 W 涤纶 T 苎麻 Ra 锦纶 P 亚麻 L 维纶 V 涤棉 T/C 涤棉/粘 T/C/R (65/35) (65/35) (50/35/15) (50/35/15) 2009-10-13 第八章纱线的主要参数
新疆大学精品课程 《纺织材料学》电子课件 2009-10-13 第八章 纱线的主要参数 第二节 常用纱线的规格与品质 一、纱线原料及标志 原料 标志符号 原料 标志符号 棉纤维 C 粘胶纤维 R 毛纤维 W 涤纶 T 苎麻 Ra 锦纶 P 亚麻 L 维纶 V 涤/棉 (65/35) T/C (65/35) 涤/棉/粘 (50/35/15) T/C/R (50/35/15)

新大典研品渠程 棉纱主要品种 《梦织树料学》电子课件 1924 名称 细度范围 适用 1.根据细度 粗特纱 >32tex 粗厚织物 中特纱 22~31tex 中厚织物 细特纱 10-21tex 细薄织物 特细特纱 5~10tex 精细面料 超细特纱 <5tex 超薄面料 普梳纱范围 针织纱 中粗特纱 2.根据用途 毛巾被单 粗特 中平布等 中特 机织纱 细平布等 细特 府绸、巴厘纱等 细特 工业用纱 中粗特纱 2009-10-13 第八章纱线的主要参数
新疆大学精品课程 《纺织材料学》电子课件 2009-10-13 第八章 纱线的主要参数 二、棉纱主要品种 1.根据细度 2.根据用途 名称 细度范围 适用 粗特纱 >32tex 粗厚织物 中特纱 22~31tex 中厚织物 细特纱 10~21tex 细薄织物 特细特纱 5~10tex 精细面料 超细特纱 <5tex 超薄面料 普梳纱范围 针织纱 中粗特纱 机织纱 毛巾被单 粗特 中平布等 中特 细平布等 细特 府绸、巴厘纱等 细特 工业用纱 中粗特纱

新程大学精品渠程 《梦织材料学》电子课件 1924 三、毛纱注要品种 毛纱品种特点: 加工系统 精梳毛纱 粗梳毛纱 半精梳毛纱 绒线 规格tex 5.5-28 50-250 10-33 针织绒细<125 手编绒线粗>142 细羊毛 纤维粗短 用细羊毛和 用羊毛和晴纶制成 纤维平直 纤维平直度差 化纤采用较 结构蓬松柔软保暖 特点 抱合紧密 茸毛多 短工艺加工 细度均匀 不光滑 性能介于前 两者之间 外观光洁 强度高 2009-10-13 第八章纱线的主要参数
新疆大学精品课程 《纺织材料学》电子课件 2009-10-13 第八章 纱线的主要参数 三、毛纱主要品种 毛纱品种特点: 加工系统 精梳毛纱 粗梳毛纱 半精梳毛纱 绒线 规格tex 5.5~28 50~250 10~33 针织绒细<125 手编绒线粗>142 特点 细羊毛 纤维平直 抱合紧密 细度均匀 外观光洁 强度高 纤维粗短 纤维平直度差 茸毛多 不光滑 用细羊毛和 化纤采用较 短工艺加工 性能介于前 两者之间 用羊毛和晴纶制成 结构蓬松柔软保暖

新大典研品渠程 《纺织材舞学》电子渠件 第三节纱线的条干均匀度 纱线的细度不匀 1.细度不匀率指标 (1)平均差系数U(现停用) 指各数据与平均数之差的绝对值的 12x- -×100% 平均值对数据平均值的百分比。 (2)变异系数CV 又称离散系数,指均方差σ对平均值x的百分比。 (当试样数n<50) CV= g-100 x-210m-10 2009-10-13 第八章纱线的主要参数
新疆大学精品课程 《纺织材料学》电子课件 2009-10-13 第八章 纱线的主要参数 第三节 纱线的条干均匀度 一、纱线的细度不匀 1. 细度不匀率指标 ⑴ 平均差系数U(现停用) 指各数据与平均数之差的绝对值的 平均值对数据平均值的百分比。 ⑵ 变异系数CV 又称离散系数, 指均方差σ 对平均值x 的百分比。 (当试样数n<50)

新程大学精品渠程 《梦织材料学》电子课件 1924 ■片段内线密度变异系数 CL)=g10,a,=1 S[x()-xa x L ■片段间质量变异系数 2k- CB(L)=2100,o,=V W-1 总变异系数 CV(L)]+[CB(L)]=[CV()]=[CB(0)] ∑X ■片段间质量变异 00 系数简化计算 CB(L)=x100= X N-1 2009-10-13 第八章纱线的主要参数
新疆大学精品课程 《纺织材料学》电子课件 2009-10-13 第八章 纱线的主要参数 ◼ 片段内线密度变异系数 ◼ 片段间质量变异系数 ◼ 总变异系数 ◼ 片段间质量变异 系数简化计算 ( ) 2 2 1 2 ( ) 100, 1 N i i x x CB L x N = − = = − ( ) 2 1 1 ( ) 100, x l x dl CV L x L − = = ( ) 2 2 1 2 ( ) 100, 1 N i i x x CB L x N = − = = − ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 0 100 100 1 i i CV L CB L CV CB X X N CB L x X N + = = − = = −