
7.3.1引言.192 7.3.2聚合物溶液理论.193 7.3.3聚合物溶液的渗透压.200 7.3.4 聚合物溶液的相平衡 202 7.3.5聚合物凝胶 205 7.4非平衡态热力学初步 7.4.1 引言 206 742局部平衡假设. 207 7.4.3 不可逆过程的熵产 . 208 7.4.4非平衡态的线性区墙 210 74.5最小熵产原理. 211 7.4.6非平衡态的非线性区域 212 7.4.7应用 213 7.5环境热力学简介. 215 7.5.1引言.215 7.5.2分配系数.215 7.5.3化学物质在环境中的分布 221 7.5.4生物体内化学物质的积累和放大效应 224 参考文就. 225 第8章常用热力学基础数据 227 8.1引言 227 8.2热力学数据杏阅方法与工具.227 8.2.1数据手册. 227 228 8.3热力学数据的估算 229 83.1对应态原理. 229 8.3.2基团贡献油 236 8.3.3混合物热力学数据的估算 259 参考文献: 265 附录 267 附录A纯物质的物理性质表 267 A-1正常沸点、临界参数和偏心因子. 26 A-2Ant0ine方程常数.,. 267 A-3修正的Rackett方程 268 A-4理想气体摩尔热容.”269 附录B三参数对应态普遍化热力学性质表. 269 B1压缩因子.*.t. 270 B2. 272 B3熵. 274
7.3. 1 引言 . . . 92 7.3.2 聚合物溶液理论 . 93 7. 3.3 聚合物溶液的渗透压 . . . 200 7.3.4 聚合物溶液的相平衡 . 202 7.3.5 聚合物凝胶 . 205 7. 4 非平衡态热力学初步 . . . 206 7. 4.1 引言 . . . 206 7. 4.2 局部平衡假设. . . . 207 7. 4.3 不可逆过程的烟产 . 20 7.4.4 非平衡态的线性区域 . . . 21 7. 4.5 最小熔产原理 . . . . 211 7. 4. 6 非平衡态的非线性区域 . 212 7.4.7 应用. . . . 213 7. 5 环境热力学简介. . 21 7. 5. 1 引言 . . . 21 7. 5.2 分配系数 . . . . . 215 7.5. 3 化学物质在环境中的分布. . 221 7. 5. 4 生物体内化学物质的积累和放大效应. . 224 参考文献. . . . . . . . . . . . . . . . . . . . . . . . . . . . 225 常用热力学基础数据. . 227 8. 1 引言 . 227 8. 2 热力学数据查阅方法与工具 . 227 8. 2.1 数据手册 . 227 8.2. 2 数据库 . 22 8. 3 热力学数据的估算 . 229 8. 3.1 对应态原理 . 229 8. 3. 2 基团贡献法 . 236 8. 3. 3 混合物热力学数据的估算 . . 259 参考文献 . . . . . . 265 附录 . 267 附录 纯物质的物理性质表 . . 267 A-1 正常沸点、临界参数和偏心因子 . . . 267 A-2 toine 方程常数. 267 A-3 修正的 ac ett 方程 . 268 A-4 理想气体摩尔热容 . . 269 附录 三参数对应态普遍化热力学性质表 . . . 269 B-1 压缩因子 . . . . 270 B-2 治. . . . 272 B-3 . . . . . 274

B-4逸度.276 B5比定压热容. 278 附录C水的性质表. 280 280 C2过热水蒸气 281 C-3过冷液体水. 284 附录D热力学性质图 285 附录E若干公式的推导. 289 E-1 式(4-69)的推导 289 E-2式(470)的推导.,. 289 E-3 证明. 290 附录F热力学性质计算软件.+.“+. 290 f-]项目. 290 F-2子菜单 291 参考文献 291 主要符号表 292
B-4 逸度. . . . . 27 B-5 比定压热容. . . 278 附录 水的性质表 . . 280 C-1 饱和水. . . . 280 习过热水蒸 . . . . . . 28 C-3 过冷液体水. . . . 84 附录 热力学性质图 . . . . . . 285 附录 若干 式的推导 . . . 289 E-1 (4 69 )的推导 . . . . . 289 之式 (4 70) 的推导 . . 289 E-3 证明. . . . 290 附录 热力学性质计算软件. . . . 290 F-1 项目 . 29 号子菜单. . . 291 参考文献 . . . . . . . . . . . . . 291 主要符号表. . . 292

第1章 绪 论 1.1目的、意义和范围 热力学的原始含义就像其英文字面(Thermo-dynamics)所示,是讨论热与功的转化规 律。经典热力学建筑在热力学的三个基本定律之上,运用数学方法,得到热力学性质之间的 依赖关系,简单地讲,这种依赖关系就是经典热力学的原理。经典热力学原理在解决工程实 际问题中有重要价值。 学习本课程的主要目的是运用经典热力学原理来解决实际问题。具体地讲,所解决的实 际问题可以归纳为三类: ①过程进行的可行性分析和能量有效利用: ②平衡问题,特别是相平衡: ③平衡状态下的热力学性质计算。 热力学性质计算在解决以上三类实际问题中都具有重要的作用,特别是流体的热力学性 质随着温度、压力、相态、组成等的变化。基于热力学原理的物性计算在本教材中将受到特 别的重视。 化工过程经常要与物性打交道。从混合物获得纯组分必须由一定的分离过程来完成,如 蒸馏、萃取、结晶等过程的基础就是相平衡及其相平衡状态下的各相的性质。研究流体相平 衡、力、V、T、焙、熵等热力学性质及其它们之间的相互关系是分离过程设计、优化和操 作中不可缺少的基础工作。化学反应过程也是同样离不开热力学性质的计算。 本课程与《物理化学》关系密切,《物理化学》的热力学部分已经介绍了经典热力学的 基本原理和理想系统(如理想气体和理想溶液等)的模型,本课程将在此基础上,重点转移 到更接近实际的系统。实际过程所涉及的系统如此复杂,温度、压力范围如此宽广,化学】 程师们不能再用简单的理想气体和理想溶液模型计算,基于分子间相互作用的理论方法尚不 完善,结合半经验模型的经典热力学仍是解决实际问题的有效手段 实际操作过程虽然不可能在平衡条件下进行,但是,代表着极限状态的热力学平衡数据 是对实际过程进行可行性分析、提高设计水平、优化操作条件不可缺少的依据 化工热力学的意义还可以从其他角度来认识。 人们有兴趣将热力学性质与压力、温度和组成等能直接测量的物理量联系起来。理论和 实验均表明,在平衡状态下,均相系统的热力学性质都能唯一地表达成压力、温度和组成的 函数(不计重力场、磁场、电场和表面张力等的影响)。温度T、压力力和组成常被选作均 相性质的独立变量。例如,均相定组成系统的摩尔体积就可以表达成为T,p的函数
1. 1 目的‘意义相范圈 热力学的原始含义就像其英文字面 (Thermo-dynamics) 所示,是讨论热与功的转化规 律。经典热力学建筑在热力学的 个基本定律之上,运用数学方法,得到热力学性质之间的 依赖关系,简单地讲,这种依赖关系就是经典热力学的原理 经典热力学原理在解决工程实 际问题中有重要价值。 学习本课程的主要目的是运用经典热力学原理来解决实际问题。具体地讲,所解决的实 际问题可以归纳为 类: ①过程进行的可行性分析和能量有效利用; 平衡问题,特别是相平衡; ③平衡状态下的热力学性质计算 热力学性质计算在解决以上三类实际问题中都具有重要的作用,特别是流体的热力学性 质随着温度、压力、相态、组成等的变化 基于热力学原理的物性计算在本教材中将受到特 别的重视。 化工过程经常要与物性打交道。从混合物获得纯组分必须由 定的分离过程来完成,如 蒸馆、萃取、结晶等过程的基础就是相平衡及其相平衡状态下的各相的性质 研究流体相平 衡、 、焰、情等热力学性质及其它们之间的相互关系是分离过程设计、优化和操 作中不可缺少的基础工作 化学反应过程也是同样离不开热力学性质的计算 本课程与 物理化学 关系密切, << 物理化学 的热力学部分己经介绍了经典热力学的 基本原理和理想系统(如理想气体和理想溶液等)的模型,本课程将在此基础上,重点转移 到更接近实际的系统 实际过程所涉及的系统如此复杂,温度、压力范围如此宽广,化学工 程师们不能再用简单的理想气体和理想溶液模型计算,基于分子间相互作用的理论方法尚不 完善,结合半经验模型的经典热力学仍是解决实际问题的有效手段 实际操作过程虽然不可能在平衡条件下进行,但是,代表着极限状态的热力学平衡数据 是对实际过程进行可行性分析、提高设计水平、优化操作条件不可缺少的依据 化工热力学的意义还可以从其他角度来认识 人们有兴趣将热力学性质与压力、温度和组成等能直接测量的物理量联系起来 理论和 实验均表明,在平衡状态下,均相系统的热力学性质都能唯一地表达成压力、温度和组成的 函数(不计重力场、磁场、电场和表面张力等的影响) 温度 、压力 和组成常被选作均 相性质的独立变量。例如,均相定组成系统的摩尔体积就可以表达成为 的函数

2化工热力学 V=V(T,p) (1-1) 同样,其他的摩尔性质M(如M=U,H,S,A,G,C.),也能相应表示为 M=M (T,p) (1-2) 式(1-1)和式(1-2)是不同性质之间的联系,经典热力学将给出它们之间的依赖关系。 从而为物性间的相互推算提供基础。物性推算是一项既有实际意义又有理论价值的工作,原 因如下 实验数据往往是不完整的。经典热力学原理给我们提供了各种热力学性质之间的依赖关 系[见式(1-2)]。这种关系对于实现不同的热力学性质之间的推算具有重要的价值。例如 从局部的实验数据推算系统完整的信息;从常温、常压下的物性数据来推算苛刻条件下的数 据;从容易获得的物性数据来推算较难测定的数据;从纯物质的性质求取混合物的性质等 所有这些都可以为我们获取有用的物性数据节省大量的人力、物力、财力和时间。 实验数据中可能存在误差。经典热力学提供的各种性质之间的普遍化关系式还是一种检 验实验数据质量的手段,从而对实验数据做出评价和筛选。 经典热力学所提供的如式(1-2)那样的方程只是规定了热力学性质恋化必须遵循的依输 关系,并非是性质之间的具体函数形式。可以想像,热力学性质之间的具体函数形式由系统 的特征所决定。系统的特征的本质是分子间的相互作用,属于统计力学的范畴。实际应用 中,常采用半经验模型来表达系统的特征。所以,经典热力学解决具体系统的物性推算问题 必须与表达系统特征的模型相结合。这是经典热力学的局限之一,但也是化工热力学解决实 际问题的特色之一 随着科学技术的高速发展,电子计算机的泛应用,自动化程度的不断提高,人们对热 力学性质需求也提出了更高的要求。如表现在热力学性质数据的高精度,不仅需要离散的 局部的信息,而且要求获得解析化的、系统的信息。所以热力学数据及模型化愈来愈受到重 视。在有些化工过程设计和模拟的计算程序中,热力学性质计算模块所占的时间已经超过 一半 从推算热力学性质所需要输入的信息量来考察,相律已经指出,一旦给定了自由度个数 的强度性质,系统的状态将被确定下来,系统的其他强度性质也随之而确定了。我们称给定 的用来确定系统的强度性质为独立变量,而系统其余的强度性质称为从属变量 由此可知。式(11)和式(1-2)中的自变量并非一定要取T,p,也可以是T,V,原则 上可以是任何两个强度性质,但是取T,p或T,V无疑是最有意义的,因为相对于其他性 质,T,p,V是最容易获得的性质,从能够直接测量的性质推算难以直接测量的性质是重 要的目标之 实际上,经典热力学还做不到仅从独立变量就能求出从属变量,原因是反映系统特征的 模型并非如此完美,需要有自由度个数之外的强度性质来辅助确定模型参数。尽管如此,经 典热力学仍然在物性推算中起到十分重要的作用。 我们可以认为,化工热力学就是运用经典热力学的原理,结合反映系统特征的模型(有 时也用强度性质数据),解决工业过程(特别是化工过程)中热力学性质的计算、相平衡和 化学平衡计算、能量的有效利用等实际问题。 1.2化工热力学的内容及安排 由上可知,经典热力学原理,必须结合反映系统特征的模型,才能应用于解决化工过程
2 I 化工 V=V(T ) (1-1) 同样,其他的摩尔性质 M( M=U ,也能相应表示 M=M ) (1-2) 式(1 1) 和式(1 2) 是不同性质之间的联系, 典热力 学将给出它们之间 的依赖关系, 从而为物性间的相互推算提供基础 物性推算是 既有实际 又有理论价值的 作,原 因如下 实验数据往往是不完整的 。经典热力学原理给我们提供了各种热力学性质之间 的依赖关 见式(1 2) ]。 这种关系对于实现不同的热力 学性质之间的推算具有重要的价值 如, 从局部的实验数据推 系统完 的信息;从常温、常压下的物性数据来 算苛刻条件下的数 据;从容易获得的物性数据来推算较难测定的数据;从纯物质的性质求取?昆合物的性质等, 所有这些都可以为我们获取有用的物性数据节省大 的人力、物力、 力和时间 实验数据中可能存在误差 。经典热力学提供的各种性质之间的普遍化关系式还是一种检 验实验数据质 的手段,从而对实验数据做出评价和筛选 经典热力学所提供的如式(1-2) 那样的方程只是规定了热力学性质变化必须遵循的依赖 关系,并非是性质之间的具体函数形式 可以想像,热力学性质之间的具体函数 式由系统 的特征所决定 系统的特征的本质是分子间的相互作用,属于统计 学的范畴 实际应 中,常采用半经验模型来表达系统的特征 所以, 典热力 学解决具体系统的物性推算问题 必须与表达系统特征的模型相结合 这是经典热力 的局限之 ,但也是 力学 决实 际问题的特色之一 科学技术 高速发展 电子计算机的广泛应用,自动 度的不断提高,人们对热 力学性质需求也提出了更高的要求。如表现在热力学性质数据的高精度,不仅 要离散的、 局部的信息,而且要求获得解析化的、系统的信息 所以热力 学数据及模型化愈来愈受到重 。在有些化工过程设计和模拟的计算程序中 热力学性质计算模 所占的时间已经超过 半。 从推算热 学性质所需 输入 信息 察, 律已 指出 旦给 了自由度个数 强度性质 系统的状态将被确定下来 系统的其他强度性质也随之 确定了 我们称 的用来确定系统的强度性质为独立变量 ,而系统其 的强度性质称为从属变量 由此可知 式(1 和式(1 2) 中的自 变量并非 定要取 ,户,也可以是 上可以 任何两个强度性质 ,但是取 无疑是 因为相对 其他性 质, 是最容易获得的性质 ,从能够直接测 的性质推 难以直接 性质是重 目标之一 实际上,经典热力学还做不到仅从独立变量就能求出从属变量,原因是反映系统特 非如此完美 需要有自 度个数之外的强度性质来辅助确定模型 管如 此, 典热力学仍然在物性推算中起到十分重要的作用 我们可以认为,化工热力 运用 典热力 原理, 结合反映系统特征的模型( 时也用强 性质数据) 解决工 过程(特别 化工过 )中热力 性质的计 、相平衡 平衡计算、能 有效利用 实际 1.2 化工热元学的内窑li 安排 由上可知, 典热力 原理 ,必须结 反映 统特征的模型 能应用于解决 工过程
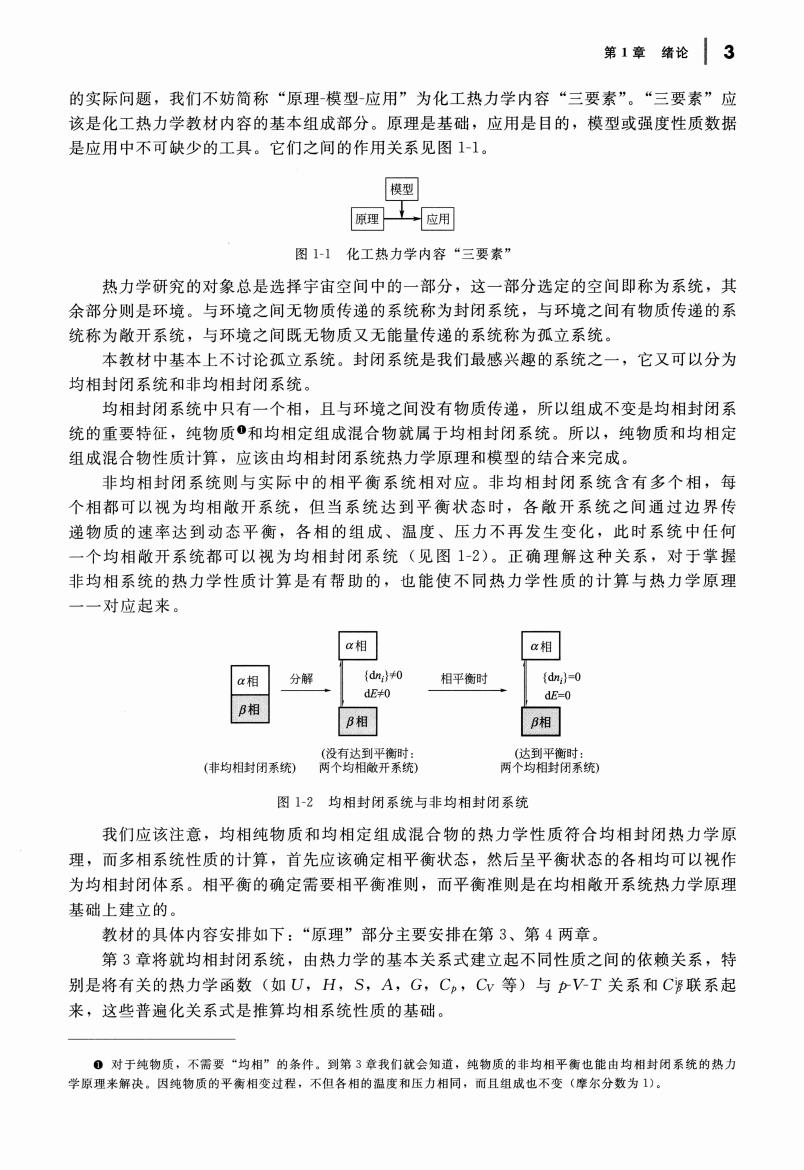
第1章绪论3 的实际问题,我们不妨简称“原理模型应用”为化工热力学内容“三要素”。“三要素”应 该是化工热力学教材内容的基本组成部分。原理是基础,应用是目的,模型或强度性质数据 是应用中不可缺少的工具。它们之间的作用关系见图1-1。 模型 保理工应用 图1-1化工热力学内容“三要索” 热力学研究的对象总是选择宇宙空间中的一部分,这一部分选定的空间即称为系统,其 余部分则是环境。与环境之间无物质传递的系统称为封闭系统,与环境之间有物质传递的系 统称为散开系统,与环境之间既无物质又无能量传递的系统称为孤立系统 本教材中基本上不讨论孤立系统。封闭系统是我们最感兴趣的系统之一,它又可以分为 均相封闭系统和非均相封闭系统。 均相封闭系统中只有一个相,且与环境之间没有物质传递,所以组成不变是均相封闭系 统的重要特征,纯物质·和均相定组成混合物就属于均相封闭系统。所以,纯物质和均相定 组成混合物性质计算,应该由均相封闭系统热力学原理和模型的结合来完成。 非均相封闭系统则与实际中的相平衡系统相对应。非均相封闭系统含有多个相,每 个相都可以视为均相敏开系统,但当系统达到平衡状态时,各散开系统之间通过边界传 递物质的速率达到动态平衡,各相的组成、温度、压力不再发生变化,此时系统中任何 ,个均相敞开系统都可以视为均相封闭系统(见图1-2)。正确理解这种关系,对于掌握 非均相系统的热力学性质计算是有帮助的,也能使不同热力学性质的计算与热力学原理 一对应起来 a相 a相 a相 分解 相平衡时 dE B相 B相 P相 (非均相封闭系统 相开 两均相闲养纺 图1-2均相封闭系统与非均相封闭系统 我们应该注意,均相纯物质和均相定组成混合物的热力学性质符合均相封闭热力学原 理,而多相系统性质的计算,首先应该确定相平衡状态,然后呈平衡状态的各相均可以视作 为均相封闭体系。相平衡的确定需要相平衡准则,而平衡准则是在均相敞开系统热力学原理 基础上建立的 教材的具体内容安排如下:“原理”部分主要安排在第3、第4两章。 第3章将就均相封闭系统,由热力学的基本关系式建立起不同性质之间的依赖关系,特 别是将有关的热力学函数(如U,H,S,A,G,Cp,Cv等)与pVT关系和C谬联系起 来,这些普遍化关系式是推算均相系统性质的基础 0对于纯物质,不需要“均相”的条件。到第3章我们就会知道,纯物质的非均相平衡也能由均相封闭系统的热力 学原理来解决。因纯物质的平衡相变过程,不但各相的湿度和压力相同,雨且组成也不变(摩尔分数为1)
章绪论 3 的实际问题,我们不妨简称"原理 模型-应用"为化工热力学内容"三要素"。"三要素"应 该是化工热力学教材内容的基本组成部分。原理是基础,应用是目的,模型或强度性质数据 是应用中不可缺少的工具 它们之间的作用关系见图 化工热力学内容" 要素" 热力学研究的对象总是选择宇宙空间中的一部分,这一部分选定的空间即称为系统,其 余部分则是环境 与环境之间无物质传递的系统称为封闭系统,与环境之间有物质传递的系 统称为敞开系统,与环境之间既无物质又无能量传递的系统称为孤立系统。 本教材中基本上不讨论孤立系统 封闭系统是我们最感兴趣的系统之一,它又可以分为 均相封闭系统和非均相封闭系统 均相封闭系统中只有一个相,且与环境之间没有物质传递,所以组成不变是均相封闭系 统的重要特征,纯物质 和均相定组成混合物就属于均相封闭系统。所以,纯物质和均相定 组成混合物性质计算,应该由均相封闭系统热力学原理和模型的结合来完成。 非均相封闭系统则与实际中的相平衡系统相对应。非均相封闭系统含有多个相,每 个相都可以视为均相敞开系统,但当系统达到平衡状态时,各敞开系统之间通过边界传 递物质的速率达到动态平衡,各相的组成、温度、压力不再发生变化,此时系统中任何 一个均相敞开系统都可以视为均相封闭系统(见图 1-2 正确理解这种关系,对于掌握 非均相系统的热力学性质计算是有帮助的,也能使不同热力学性质的计算与热力学原理 一一对应起来 国主巴 相平衡时 (没有达到平衡时 (达到平衡时 (非均相封闭系统) 两个均相敞开系统) 两个均相封闭系统) 均相封闭系统与非均相封闭系统 我们应该注意,均相纯物质和均相定组成混合物的热力学性质符合均相封闭热力学原 理,而多相系统性质的计算,首先应该确定相平衡状态,然后呈平衡状态的各相均可以视作 为均相封闭体系 相平衡的确定需要相平衡准则,而平衡准则是在均相敞开系统热力学原理 基础上建立的 教材的具体内容安排如下"原理"部分主要安排在第 、第 两章。 章将就均相封闭系统,由热力学的基本关系式建立起不同性质之间的依赖关系,特 别是将有关的热力学函数(如 H , S , A , G, Cv 等)与 p- 关系和 01 联系起 来,这些普遍化关系式是推算均相系统性质的基础 对于纯物质,不需 "均相"的条件 到第 我们就 知道,纯物质的非均相平衡也能由均相封闭系统的热力 原理来解决 因纯物质的平衡相 过程,不但各相的温度和压力相同,而且组成也不变(摩尔分数为