
/依次处理a表中的数据元素 for (int i =1;i<=La.Count()-1;++i) intj▣g; /查看b表中有无与a表中相同的数据元素 for (j=0;j<=Lb.Count()-1;++j) /有相同的数据元素 if (La.getdata(i)==Lb.getdata(j)) break; 1 //没有相同的数据元素, /将a表中的数据元素附加到b表的末尾。 if(j Lb.Count()-1) Lb.Append(La.getdata(i)); Lb.printlist(); return Lb; 算法的时间复杂度是O(m*n,m是La的表长,n是Lb的表长。 线性表采用顺序存储方式时缺点: (1)需要一组编号连续的存储单元 线性表的顺序存储:把线性表的数据元素放在一组编号连续的存储单元中。但是,计算 机的内存里往往有很多小的空间。线性表L采用顺序存储时这些零碎的小空间得不到充分利 用。 (2)删除、插入操作需大量移动数据元素。 为克服这两个缺点,下一节讨论线性表的另一种存储方式链式存储。 2.3线性表的链式表示和实现 2.3.1基本术语 1.线性表的链式存储 3
31 //依次处理 a 表中的数据元素 for (int i =1; i <= La.Count() - 1; ++i) { int j = 0; //查看 b 表中有无与 a 表中相同的数据元素 for (j = 0; j <= Lb.Count() - 1; ++j) { //有相同的数据元素 if (La.getdata(i)==Lb.getdata(j)) { break; } } //没有相同的数据元素, //将 a 表中的数据元素附加到 b 表的末尾。 if(j > Lb.Count()- 1) { Lb.Append(La.getdata(i)); } } Lb.printlist(); return Lb; } 算法的时间复杂度是O(m*n),m是La的表长,n是Lb的表长。 线性表采用顺序存储方式时,缺点: (1)需要一组编号连续的存储单元 线性表的顺序存储:把线性表的数据元素放在一组编号连续的存储单元中。但是,计算 机的内存里往往有很多小的空间。线性表 L 采用顺序存储时这些零碎的小空间得不到充分利 用。 (2)删除、插入操作需大量移动数据元素。 为克服这两个缺点,下一节讨论线性表的另一种存储方式-链式存储。 2.3 线性表的链式表示和实现 2.3.1 基本术语 1.线性表的链式存储
线性表的链式存储是指用一组任意的存储单元(可以不连续)存储线性表中的数据元素。 以线性表L=(A,B.C)为例,对比着讲。 L(,B,C)数据类型是字符型,字符型数据占用一个存储单元,即一个字节。 线性表的顺序存储是指用一组连续的存储单元存储线性表中的数据元素。采用顺序存储 方式时,数据的存储是有规律的,计算机可以通过数据元素自身的地址计算出它的后继元素 地址,从而找到它的后继元素 A B . L 假设数据元素A的存储地址是L,它的后继元素的存储地址是:L+L,L+】地址里面存放着 B,表明A的后继元素就是B 己知数据元素B的存储地址是L+1,它的后继元素的存储地址是L+2. L+2地址里面存放着C,表明B的后继元素就是C 线性表采用链式存储时是用一组任意的存储单元存放它的数据元素,数据的存储毫无规 律可言,计算机通过数据元素自身的地址无法计算出它的后继元素地址,从而无法找到它的 后继元素是谁。 .C A B 8 64 128 所以,我们需要在它的后面附加一个指针域(引用域),存储它的后继元素的地址,指向它 的后继元素。 C NULL .A128 .B8. 8 64 128 查找元素后继时,利用指针(引用)提供的后继元素地址,从而找到它的后继元素。 例如: 数据元素A,利用指针提供的后继元素地址128,可以确认它的后继是B。 数据元素B,利用指针提供的后继元素地址8,可以确认它的后继是C。 从此可以看出链式存储的一个优点:线性表的数据元素不必放在地址连续的存储单元中, 零碎空间能得到充分的利用。 在JAVA语言中,内存单元的编号8,64,128对用户屏蔽(也就是8,64,128不需要
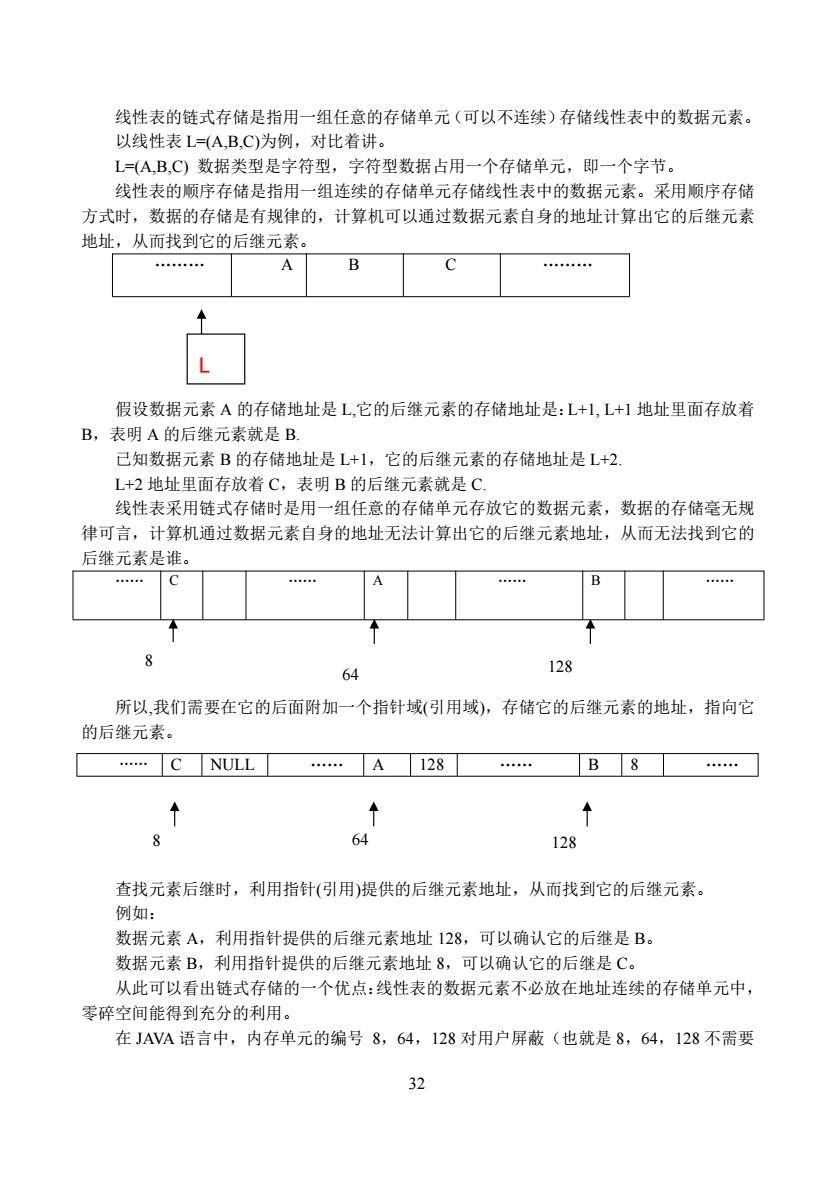
32 线性表的链式存储是指用一组任意的存储单元(可以不连续)存储线性表中的数据元素。 以线性表 L=(A,B,C)为例,对比着讲。 L=(A,B,C) 数据类型是字符型,字符型数据占用一个存储单元,即一个字节。 线性表的顺序存储是指用一组连续的存储单元存储线性表中的数据元素。采用顺序存储 方式时,数据的存储是有规律的,计算机可以通过数据元素自身的地址计算出它的后继元素 地址,从而找到它的后继元素。 . A B C . L 假设数据元素 A 的存储地址是 L,它的后继元素的存储地址是:L+1, L+1 地址里面存放着 B,表明 A 的后继元素就是 B. 已知数据元素 B 的存储地址是 L+1,它的后继元素的存储地址是 L+2. L+2 地址里面存放着 C,表明 B 的后继元素就是 C. 线性表采用链式存储时是用一组任意的存储单元存放它的数据元素,数据的存储毫无规 律可言,计算机通过数据元素自身的地址无法计算出它的后继元素地址,从而无法找到它的 后继元素是谁。 . C . A . B . 所以,我们需要在它的后面附加一个指针域(引用域),存储它的后继元素的地址,指向它 的后继元素。 查找元素后继时,利用指针(引用)提供的后继元素地址,从而找到它的后继元素。 例如: 数据元素 A,利用指针提供的后继元素地址 128,可以确认它的后继是 B。 数据元素 B,利用指针提供的后继元素地址 8,可以确认它的后继是 C。 从此可以看出链式存储的一个优点:线性表的数据元素不必放在地址连续的存储单元中, 零碎空间能得到充分的利用。 在 JAVA 语言中,内存单元的编号 8,64,128 对用户屏蔽(也就是 8,64,128 不需要 . C NULL . A 128 . B 8 . 8 64 128 8 64 128

我们知道),线性表的链式存储结构可以用如下形式表示: A →B NULL 箭头代表指针(引用),指向下一个元素的存储位置 一个蓝色的方块称为一个结点,它包含数据和指针(引用)两部分。 2.结点:数据和指针(引用)的组合。 Data next 数据部分命名为data:用米存放线性表中数据元素。 指针(引用)部分命名为next:存放下一个结点的地址: 3.链表:整个线性表的链式存储结构,上述两个箭头连接的三个方块称之为一个链表。 L=(a1,a2,am)的链式存储结构如下图所示: am→a2→ +anΛ 只要我们知道第一个结点的地址,找到第一个元素,我们就能顺藤摸瓜,找到线性表的 所有元素。这个地址称为线性表的头指针,书上用head表示。 head +a→a2 anΛ 为了操作上的方便,可以在第一个结点之前增加一个头结点。头结点的类型与其他结点 ·样,分为数据部分和引用(指针)部分。头结点的数据部分为空或存放线性表的元素个数 头结点的引用(指针)指向线性表的第一个数据元素。 head-→an□a .anΛ 带头结点的链表 以下基本操作的实现都是在带头结点的链表存储结构下实现的,带头结点的链表怎麽个 方便法,以删除操作为例来讲。 带头结点的链表中删除第一个元素:head指针不用变:带头结点的链表中删除其他元素: hcad指针也不用变。带头结点的链表存储结构处理第一个元素的操作不存在特殊性。 不带头结点的链表中别除第一个元素al,需要修改hcad指针为第二个结点的地址。不 33
33 我们知道),线性表的链式存储结构可以用如下形式表示: A B C NULL 箭头代表指针(引用),指向下一个元素的存储位置 一个蓝色的方块称为一个结点,它包含数据和指针(引用)两部分。 2.结点:数据和指针(引用)的组合。 数据部分命名为 data:用来存放线性表中数据元素。 指针(引用)部分命名为 next:存放下一个结点的地址。 3.链表:整个线性表的链式存储结构,上述两个箭头连接的三个方块称之为一个链表。 L= (a , a ,., a ) 1 2 n 的链式存储结构如下图所示: a1 a2 an ∧ 只要我们知道第一个结点的地址,找到第一个元素,我们就能顺藤摸瓜,找到线性表的 所有元素。这个地址称为线性表的头指针,书上用 head 表示。 head a1 a2 an ∧ 为了操作上的方便,可以在第一个结点之前增加一个头结点。头结点的类型与其他结点 一样,分为数据部分和引用(指针)部分。头结点的数据部分为空或存放线性表的元素个数。 头结点的引用(指针)指向线性表的第一个数据元素。 head a1 a2 an ∧ 以下基本操作的实现都是在带头结点的链表存储结构下实现的,带头结点的链表怎麽个 方便法,以删除操作为例来讲。 带头结点的链表中删除第一个元素:head 指针不用变;带头结点的链表中删除其他元素: head 指针也不用变。带头结点的链表存储结构处理第一个元素的操作不存在特殊性。 不带头结点的链表中删除第一个元素 a1,需要修改 head 指针为第二个结点的地址。不 Data next next 带头结点的链表
带头结点的链表中别除其他元素:head指针不用变:处理第一个元素的操作存在特殊性。 接下来讨论在链式存储结构下基本操作的实现。因为插入和删除操作较为重要,相对来 说也比较复杂,先重点分析一下插入和删除两种操作。 2.3.2链式存储结构下基本操作分析 1.删除操作线性表L中删除第ⅰ个元素 链式存储结构下从链表中把第ⅰ个结点摘除即可。 +1 (1)找到第l个结点r和第i个结点p (2)令i-l个结点r的引用(指针)域指向第i+1个结点:第i-1个元素的后继就成了i+1, 第ⅰ个元素就从线性表中删除了 (3)释放第ⅰ个结点所占用的内存空间 链式存储结构下删除操作效率分析:只需修改一次指针;不论线性表多大,即使10000个 元素,也还是修改一次指针。 ·插入操作(前插)在线性表的第ⅰ个位置插入数据元素x 链式存储结构下也就是在链表的第ⅰ个位置插入结点q i+1 34
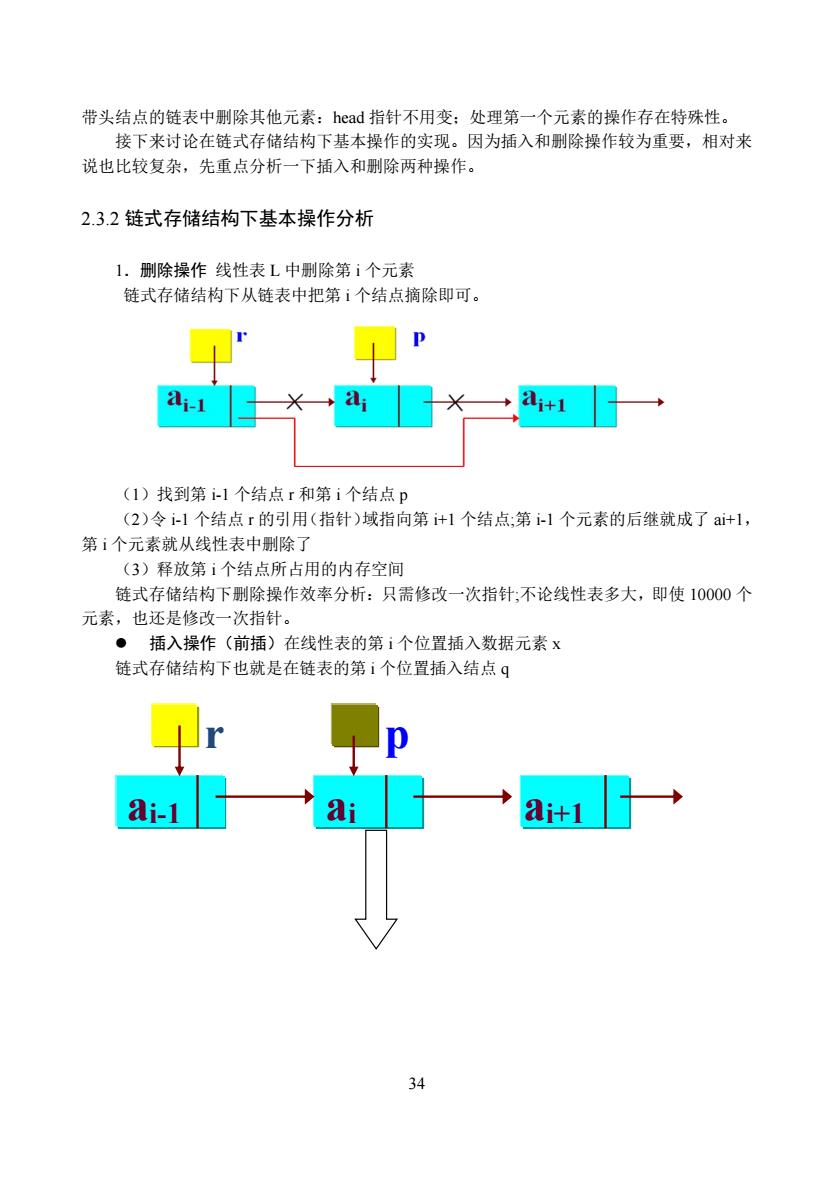
34 带头结点的链表中删除其他元素:head 指针不用变;处理第一个元素的操作存在特殊性。 接下来讨论在链式存储结构下基本操作的实现。因为插入和删除操作较为重要,相对来 说也比较复杂,先重点分析一下插入和删除两种操作。 2.3.2 链式存储结构下基本操作分析 1.删除操作 线性表 L 中删除第 i 个元素 链式存储结构下从链表中把第 i 个结点摘除即可。 (1)找到第 i-1 个结点 r 和第 i 个结点 p (2)令 i-1 个结点 r 的引用(指针)域指向第 i+1 个结点;第 i-1 个元素的后继就成了 ai+1, 第 i 个元素就从线性表中删除了 (3)释放第 i 个结点所占用的内存空间 链式存储结构下删除操作效率分析:只需修改一次指针;不论线性表多大,即使 10000 个 元素,也还是修改一次指针。 插入操作(前插)在线性表的第 i 个位置插入数据元素 x 链式存储结构下也就是在链表的第 i 个位置插入结点 q r p ai-1 ai ai+1

i-1 q (1)建立新结点q,令q的数据域等于x (2)找到第-1个结点r和第i个结点p (3)令第-1个结点r的指针域指向新结点q, 令新结点g的指针域指向结点P 这样a-l的后继就成了x,x的后继就成了ai,成功得在线性表的第i个位置插入了数 据元素x 效率分析:只需修改两次指针, 不论线性表多大,即使10000个元素,也还是修改两次指针。 2.3.3源码实现 1.几点说明 (1)线性表的数据类型是T: (2)结点的表示 数据和引用的组合。因为是两项的组合,所以我们用一个类来表示:类中包含data和next 两项 Data next public class Node<T> public Tdata:/lW数据部分,存放线性表的某一个数据元素 public Node<T>next;∥引用部分,指示下一个结点的地址 (3)线性表的表示
35 (1)建立新结点 q,令 q 的数据域等于 x (2)找到第 i-1 个结点 r 和第 i 个结点 p (3)令第 i-1 个结点 r 的指针域指向新结点 q , 令新结点 q 的指针域指向结点 p 这样 ai-1 的后继就成了 x,x 的后继就成了 ai,成功得在线性表的第 i 个位置插入了数 据元素 x 效率分析:只需修改两次指针; 不论线性表多大,即使 10000 个元素,也还是修改两次指针。 2.3.3源码实现 1.几点说明: (1)线性表的数据类型是 T; (2)结点的表示 数据和引用的组合。因为是两项的组合,所以我们用一个类来表示:类中包含 data 和 next 两项.public class Node<T> { public T data; ///数据部分,存放线性表的某一个数据元素 public Node<T> next; // 引用部分,指示下一个结点的地址 }; (3)线性表的表示 Data next next