
方差分析的具体做法 1.这种方法是将k个处理的观测值作为一个整体 看待; 2.把观测值总变异的平方和及自由度分解为相应 于不同变异来源的平方和及自由度,进而获得不 同变异来源总体方差估计值: 3.通过计算这些总体方差的估计值的适当比值, 就能检验各样本所属总体平均数是否相等
1.这种方法是将 k 个处理的观测值作为一个整体 看待; 2.把观测值总变异的平方和及自由度分解为相应 于不同变异来源的平方和及自由度,进而获得不 同变异来源总体方差估计值; 3. 通过计算这些总体方差的估计值的适当比值, 就能检验各样本所属总体平均数是否相等。 方差分析的具体做法
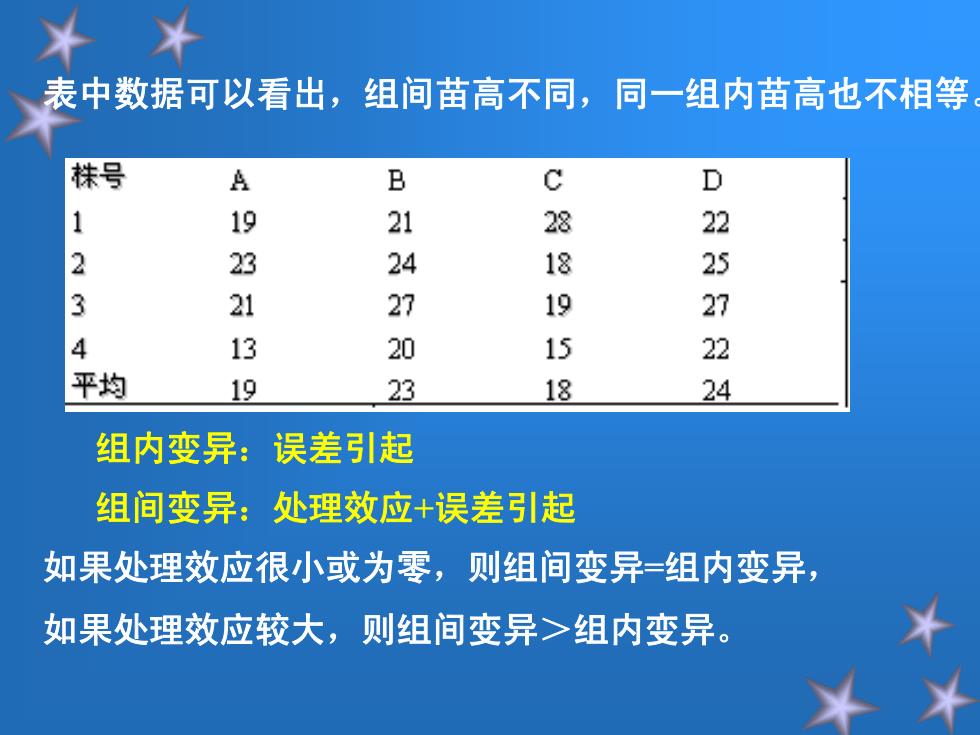
表中数据可以看出,组间苗高不同,同一组内苗高也不相等 株号 A B C D 1 19 21 28 22 2 23 24 18 25 3 21 27 19 27 4 13 20 15 22 平均 19 23 18 24 组内变异: 误差引起 组间变异:处理效应+误差引起 如果处理效应很小或为零,则组间变异=组内变异, 如果处理效应较大,则组间变异>组内变异
表中数据可以看出,组间苗高不同,同一组内苗高也不相等 。 组内变异:误差引起 组间变异:处理效应 +误差引起 如果处理效应很小或为零,则组间变异 =组内变异, 如果处理效应较大,则组间变异>组内变异

Question:怎样比较两个变异的大小? 才
Question:怎样比较两个变异的大小?

比较两个方差的齐性-F检验 σ组内是随机误差σ2 2 组间 组内 σ2组间是随机误差+处理效应 组间 组内 Ho: 处理效应为零 O组内 2 则 组间 2 D组内 当F>Fa时,P<0.05,拒绝H,处理效应显著。 当F<Fa时,P>0.05,接受H,处理效应不显著 哪种处理效果最好?做平均数间的两两比较多重比较
2组内 是随机误差2 2组间 是随机误差+处理效应 HO:处理效应为零 则 当F> F时,P<0.05 , 拒绝H0 ,处理效应显著。 当F< F时,P>0.05 ,接受H0 ,处理效应不显著. 哪种处理效果最好?做平均数间的两两比较-多重比较。 2 2 2 2 S S F 组间 组内 组间 组内 222 组间 组内 2 2 S F S 组间 组内 比较两个方差的齐性-F检验

方差分析的基本出发点在变异性上,故叫做 方差分析。 基本思路是分析变异产生的来源,构建它 们的方差,利用F检验来分析各组平均数之 间的差异显著性
方差分析的基本出发点在变异性上,故叫做 方差分析。 基本思路是分析变异产生的来源,构建它 们的方差,利用F检验来分析各组平均数之 间的差异显著性