《数据库系统概念 Database System Concepts》原书教学资源（第五版，PPT课件讲稿，英文版）Chapter 14 Query Optimization

Equivalence Rules (Cont.) 8.The projection operation distributes over the theta join operation as follows: (a)if 0 involves only attributes from L1L2: Πu,(E凶gE2)=(Π，(E)凶g(Π，(E2) (b)Consider a join E1NXe E2. Let L1 and L2 be sets of attributes from E1 and E2,respectively. Let L3 be attributes of E1 that are involved in join condition 0,but are not in LL2,and let L be attributes of E2 that are involved in join condition 0,but are not in L1 L2. Πu,(E,凶gE2)=Πu(Πu(E)凶（Π2u,(E2) Database System Concepts-5thEdition,Oct 5,2006. 14.12 @Silberschatz,Korth and Sudarshan

Database System Concepts - 5 14.12 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Equivalence Rules (Cont.) 8. The projection operation distributes over the theta join operation as follows: (a) if  involves only attributes from L1  L2 : (b) Consider a join E1  E2 . Let L1 and L2 be sets of attributes from E1 and E2 , respectively. Let L3 be attributes of E1 that are involved in join condition , but are not in L1  L2 , and let L4 be attributes of E2 that are involved in join condition , but are not in L1  L2 . ( ) ( ( )) ( ( )) L1L2 E1 E2 = L1 E1  L2 E2 ( ) (( ( )) ( ( ))) L1L2 E1 E2 L1L2 L1L3 E1 L2 L4 E2  =  

Equivalence Rules (Cont.) 9.The set operations union and intersection are commutative E10E2=E2UE1 E1∩E2=E2∩E1 (set difference is not commutative). 10.Set union and intersection are associative. (E10E2)UE3=E10(E2UE3) (E1∩E2)∩E3=E1∩(E2∩E3) 11.The selection operation distributes over and-. 0(E1-E2)=0(E1)-σ(E2) and similarly for and in place of Also: O6(E1-E2)=O(E1)-E2 and similarly for in place of -but not for 12.The projection operation distributes over union Π(E1UE2)=(Π(E1)U((E2) Database System Concepts-5th Edition,Oct 5,2006. 14.13 ©Silberschat乜，Korth and Sudarshan

Database System Concepts - 5 14.13 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Equivalence Rules (Cont.) 9. The set operations union and intersection are commutative E1  E2 = E2  E1 E1  E2 = E2  E1 (set difference is not commutative). 10. Set union and intersection are associative. (E1  E2 )  E3 = E1  (E2  E3 ) (E1  E2 )  E3 = E1  (E2  E3 ) 11. The selection operation distributes over ,  and –.  (E1 – E2 ) =  (E1 ) –  (E2 ) and similarly for  and  in place of – Also:  (E1 – E2 ) =  (E1 ) – E2 and similarly for  in place of –, but not for  12. The projection operation distributes over union L (E1  E2 ) = (L (E1 ))  (L (E2 ))

Transformation Example:Pushing Selections Query:Find the names of all customers who have an account at some branch located in Brooklyn. IIcustomer_name(pranch_city=Brooklyn (branch (account depositor))) Transformation using rule 7a. Πcustomer_name (branch_city=Brooklyn(branch)) ☒(account凶depositor) Performing the selection as early as possible reduces the size of the relation to be joined. Database System Concepts-5th Edition,Oct 5,2006. 14.14 ©Silberschat乜，Korth and Sudarshan

Database System Concepts - 5 14.14 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Transformation Example: Pushing Selections Query: Find the names of all customers who have an account at some branch located in Brooklyn. customer_name(branch_city = “Brooklyn” (branch (account depositor))) Transformation using rule 7a. customer_name ((branch_city =“Brooklyn” (branch)) (account depositor)) Performing the selection as early as possible reduces the size of the relation to be joined

Example with Multiple Transformations Query:Find the names of all customers with an account at a Brooklyn branch whose account balance is over $1000. IIcustomer_name(branch_city=Brooklyn"balance>1000 (branch (account depositor))) Transformation using join associatively(Rule 6a): IIcustomer_name(branch_city="Brooklyn"balance>1000 (branch☒account)X depositor） Second form provides an opportunity to apply the"perform selections early"rule,resulting in the subexpression branch_city='Brooklyn"(branch)balance>1000(account) Thus a sequence of transformations can be useful Database System Concepts-5th Edition,Oct 5,2006. 14.15 ©Silberschat乜，Korth and Sudarshan

Database System Concepts - 5 14.15 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Example with Multiple Transformations Query: Find the names of all customers with an account at a Brooklyn branch whose account balance is over $1000. customer_name( (branch_city = “Brooklyn”  balance > 1000 (branch (account depositor))) Transformation using join associatively (Rule 6a): customer_name((branch_city = “Brooklyn”  balance > 1000 (branch account)) depositor) Second form provides an opportunity to apply the “perform selections early” rule, resulting in the subexpression branch_city = “Brooklyn” (branch)  balance > 1000 (account) Thus a sequence of transformations can be useful

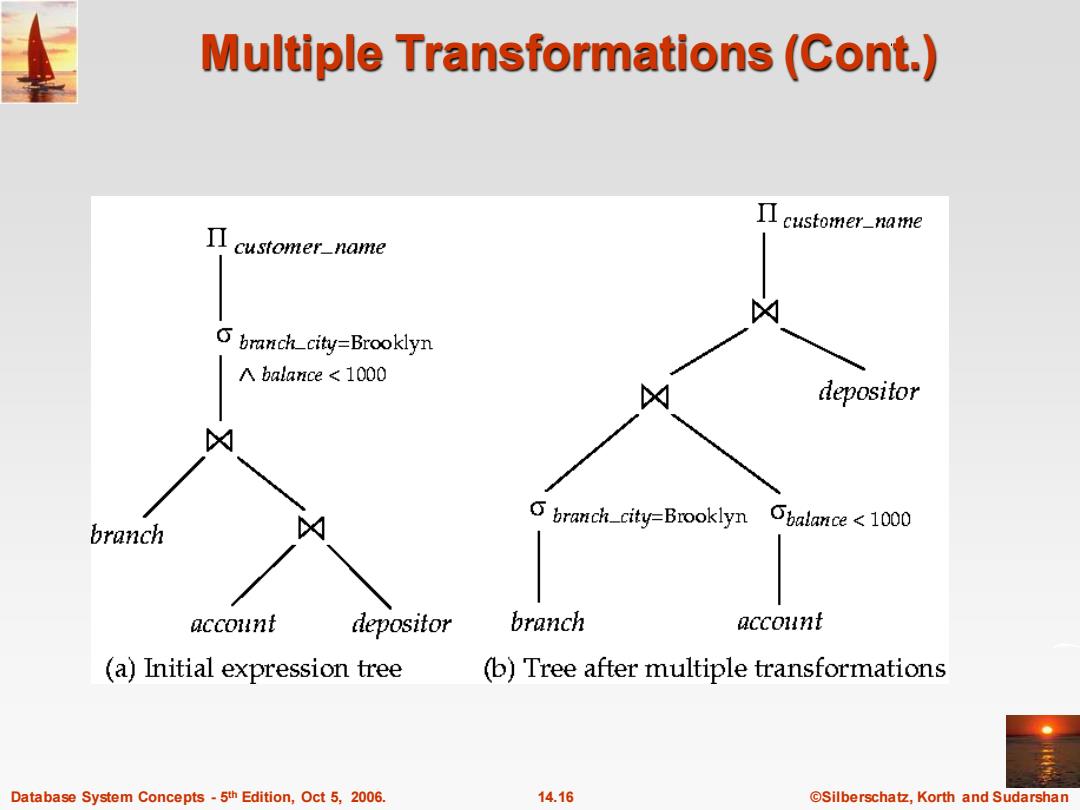
Multiple Transformations(Cont.) customer_name Π customer_name branch_city=Brooklyn A balance 1000 depositor branch_city=Brooklyn Obalance<1000 branch account depositor branch account (a)Initial expression tree (b)Tree after multiple transformations Database System Concepts-5th Edition,Oct 5,2006. 14.16 ©Silberschat乜，Korth and Sudarshan

Database System Concepts - 5 14.16 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Multiple Transformations (Cont.)