
Limited Dependency ·k-CNF:Φ=C1AC2A…∧Cm k variables Φ=(x1Vx2Vx3)Λ(x1Vx2Vx4)A(3Vx4Vx5) Dependency degree d: each clause intersects d other clauses uniform random1,...,[T,F),each clause is violated w.p.2- (union bound)m2-k<1 → Pr[no clause is violated ]>0 LLL)e(d+1)2-k≤1 4d2-k≤1
• -CNF: • uniform random , each clause is violated w.p. k Φ = C1 ∧ C2 ∧ ⋯ ∧ Cm Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) x1, …, xn ∈ {�, �} 2−k Limited Dependency k variables ⟹ Pr[ no clause is violated ] > 0 (union bound) m2−k < 1 } (“local” union bound?) d2−k < 1 (LLL) e(d + 1)2−k ≤ 1 Dependency degree : each clause intersects other clauses d ≤ d 4d2−k ≤ 1

Lovasz Local Lemma (LLL) ·“Bad"events A1,,Am,where all Pr[A]≤p Dependency degree d: each A;is“dependent"of≤d other events Lovasz Local Lemma [Lovasz and Erd6s 1973;Lovasz 1977]: ep(d+)≤1→ ·The“LLL”condition: Bad events are not too possible to occur individually. Bad events are not too dependent with each other
Lovász Local Lemma [Lovász and Erdős 1973; Lovász 1977]: ep(d + 1) ≤ 1 • “Bad” events A , where all 1,…, Am Pr[Aj ] ≤ p Lovász Local Lemma (LLL) ⟹ Pr [ m ⋀ i=1 Ai ] > 0 Dependency degree : each is “dependent” of other events d Ai ≤ d • The “LLL” condition: • Bad events are not too possible to occur individually. • Bad events are not too dependent with each other

Dependency Graph .“Bad"events A1,,Am Dependency degree d: each A;is mutually independent of all except d other events Definition(independence): A is independent of B if Pr[A B]Pr[A]or B is impossible. Ao is mutually independent of A1,...,Am if Ao is independent of every event B=B1A…ΛBnm,where each B=A;orAi
• “Bad” events A , 1,…, Am Dependency Graph Dependency degree : each is mutually independent of all except other events d Ai ≤ d Definition (independence): is independent of if or is impossible. is mutually independent of if is independent of every event , where each or . A B Pr[A ∣ B] = Pr[A] B A0 A1, …, Am A0 B = B1 ∧ ⋯ ∧ Bm Bi = Ai Ai
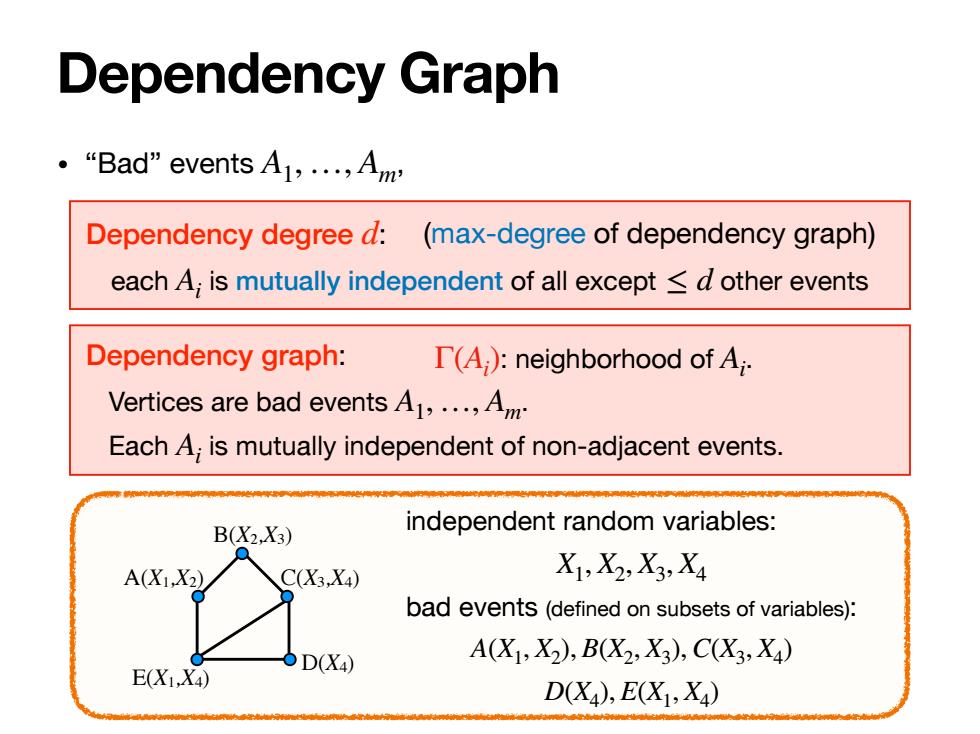
Dependency Graph 。Bad"events A1,,Am Dependency degree d:(max-degree of dependency graph) each A;is mutually independent of all except d other events Dependency graph: T(A,):neighborhood of A; Vertices are bad events A1,....A Each A;is mutually independent of non-adjacent events. B(X2.X3) independent random variables: A(X1,X2) C(X3,X4) X1,X2,X3,X4 bad events (defined on subsets of variables): E(X1,Xa) D(X4) A(X1,X2),B(X2,X3),CX3,X4) D(X4),E(X1,X4)
Dependency Graph Dependency degree : each is mutually independent of all except other events d Ai ≤ d Dependency graph: Vertices are bad events . Each is mutually independent of non-adjacent events. A1, …, Am Ai (max-degree of dependency graph) A(X1,X2) B(X2,X3) C(X3,X4) E(X1,X4) D(X4) independent random variables: bad events (defined on subsets of variables): X1, X2, X3, X4 A(X1, X2), B(X2, X3),C(X3, X4) D(X4), E(X1, X4) Γ(A : neighborhood of . i ) Ai • “Bad” events A , 1,…, Am

Lovasz Local Lemma (LLL) A1,...,A has a dependency graph given by neighborhoods I(): A;is mutually independent of all A;(A) Lovasz Local Lemma: p≌max;Pr[Ai]and d≌max;|(Al ep(d+1)≤1→Pr[∧1A>0
Lovász Local Lemma: p ≜ max and i Pr[Ai ] d ≜ maxi |Γ(Ai )| ep(d + 1) ≤ 1 ⟹ Pr[⋀m i=1Ai] > 0 Lovász Local Lemma (LLL) • has a dependency graph given by neighborhoods : is mutually independent of all A1, …, Am Γ( ⋅ ) Ai Aj ∉ Γ(Ai )