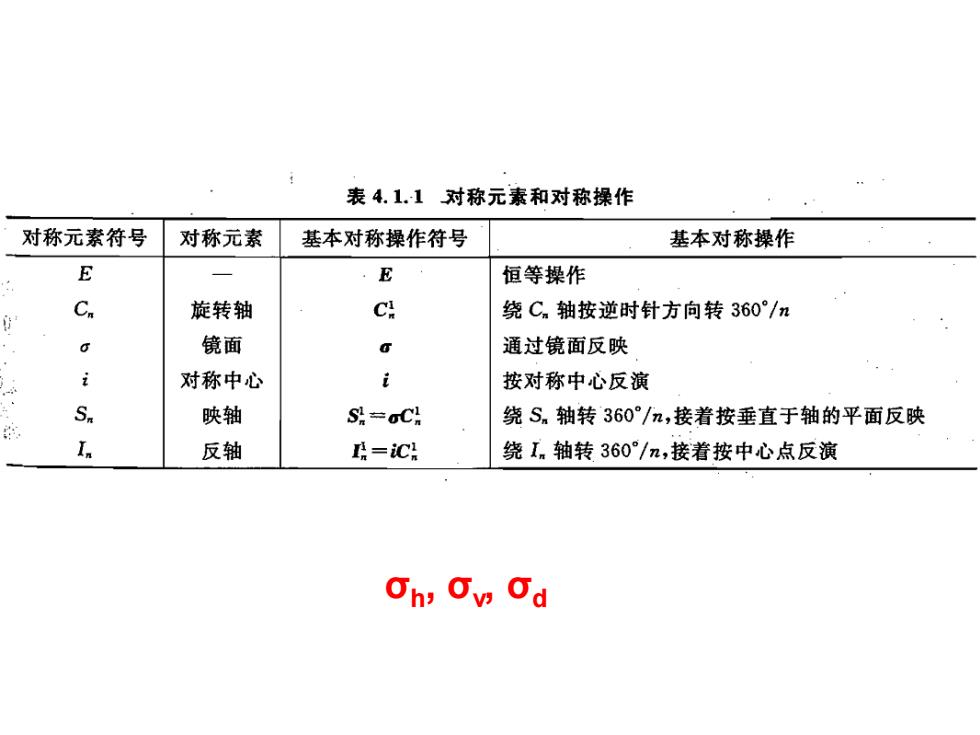
表4.1.1对称元素和对称操作 对称元素符号 对称元素 基本对称操作符号 基本对称操作 E E 恒等操作 C. 旋转轴 c 绕C.轴按逆时针方向转360°/n 镜面 6 通过镜面反映 对称中心 按对称中心反演 Sn 映轴 S.=oCl 绕S.轴转360°/n,接着按垂直于轴的平面反映 反轴 县=C 绕In轴转360°/n,接着按中心点反演 Oh,Ov Od
σh , σv , σd

七种晶系 对称条件 晶系 1(E)或1() 三斜、七个晶系:根据晶胞的类型,找相应特征对称元素,可以把 32个点群划分为七个晶系。特征对称元素中,高轴次的个 2(C2)或2(m) 单斜 数愈多,对称性高。晶系从对称性由高到低的划分。 两个2(c2)或2(m) 正交 划分的法:首先规定每个晶系的特征对称元素,不是该晶系 的晶体的全部对称元素,而是一些有代表性的对称元素(该晶 系所有点群共有的对称元素), 4(C4)或4S43) 四方 例如,立方晶系的特征对称元素是4条沿正方体体对角线3; 3(C3)或3S65) 三方 六方晶系特征对称元素是六重对称轴(包括旋转轴、螺旋轴或反轴) 然后,将晶体归入对称性尽可能高的晶系。对称性最高的晶系是 立方晶系,依次往下是六方、四方、三方、正交、单斜、三斜. 6(C6)或6(S35) 六方 每个品系的品胞都是具有特定边角关系的平行六面体.每种晶系 四个三次轴 立方 都有自己的特征对称元素,相应地就有一定的晶胞类型
七种晶系 对称条件 晶系 特点 四个三次轴 三 斜 单 斜 正 交 四 方 三 方 六 方 立 方 1(E)或1(i) 2(C2 )或2(m) 两个2(C2 )或2(m) 4(C4 )或4(S4 3 ) 3(C3 )或3(S6 5 ) 6(C6 )或6(S3 5 ) a ≠ b ≠ c, ≠ ≠ a ≠ b ≠ c, = = 90o ≠ a ≠ b ≠ c, = = = 90o a = b ≠ c, = = = 90o a = b ≠ c, = = 90o , = 120o a = b = c, = = = 90o a = b = c, = = 菱形 a = b ≠ c, = = 90o , = 120o
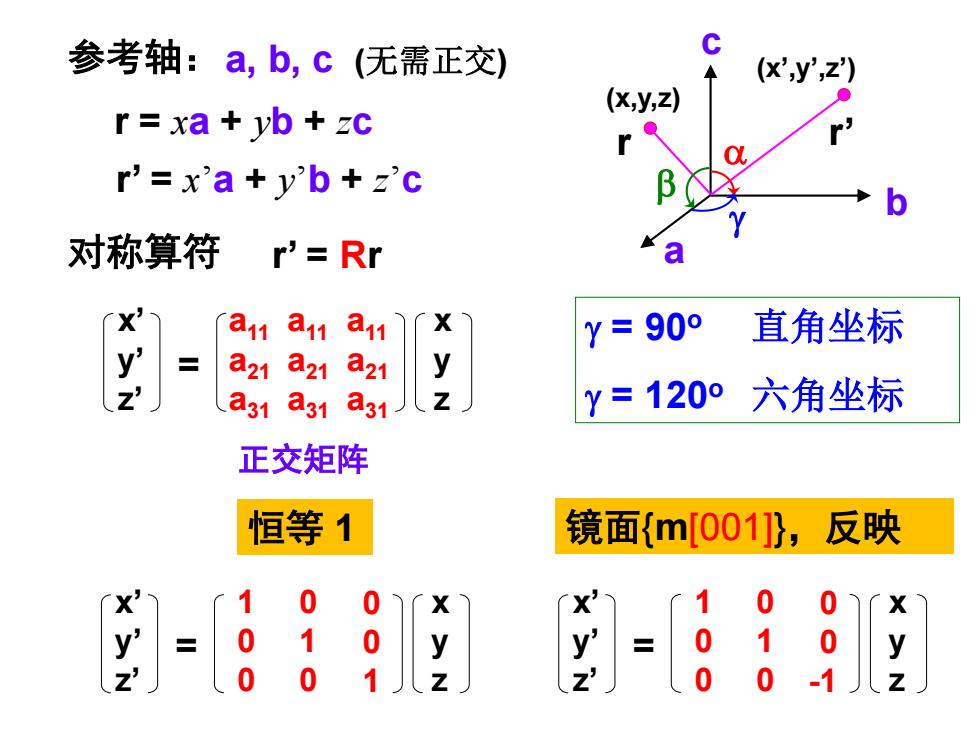
参考轴:a,b,c(无需正交) (x',y,z) (x,y,z) r=xa+yb+zc r'=x'a+y'b+z'c 对称算符 r'=Rr a a11 a11a11 Y=90° 直角坐标 y a21a21a21 y a31a31a31 Y=120°六角坐标 正交矩阵 恒等1 镜面{m001},反映 xy 1 0 0 0 1 y 1 0 0 7 0 1
恒等 1 镜面{m[001]},反映 x’ y’ z’ x y z -1 -0 -0 -0 -1 -0 -0 -0 -1 = x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 参考轴: 对称算符 r’ = Rr a, b, c (无需正交) x’ y’ z’ x y z a11 a21 a31 a11 a21 a31 a11 a21 a31 = r = xa + yb + zc r’ = x’a + y’b + z’c (x,y,z) (x’,y’,z’) r r’ a b c = 90o 直角坐标 = 120o 六角坐标 正交矩阵
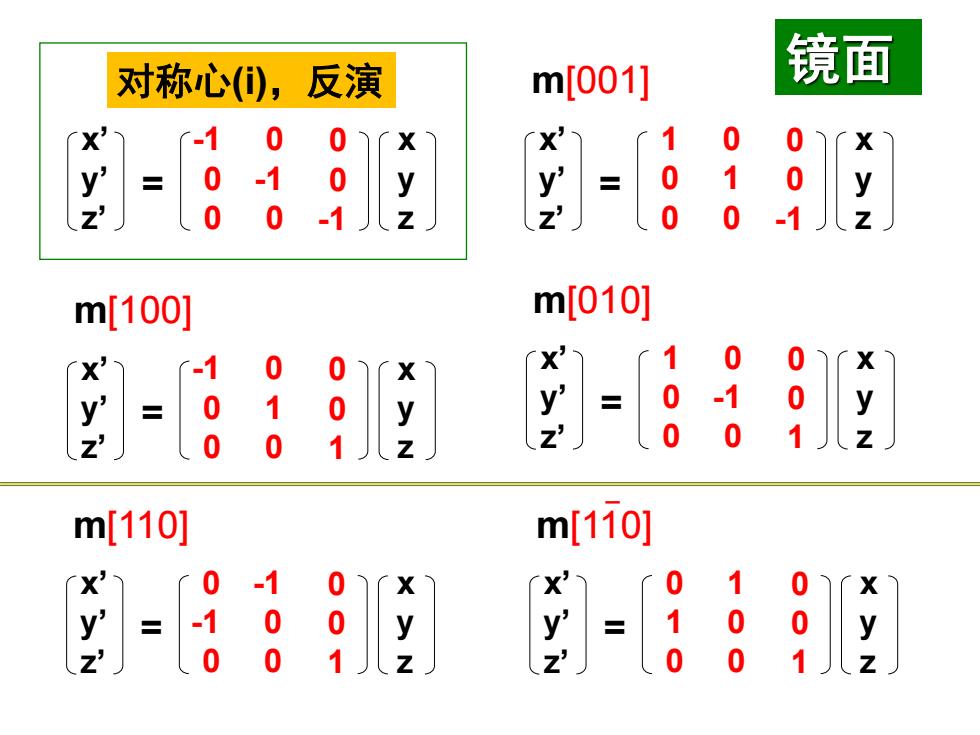
对称心①,反演 m[001] 镜面 1 0 X' 1 0 0 0 1 0 0 -1 0 0 .1 m[100] m[010] -1 0 0 1 0 X 0 y 0 1 0 0 -1 0 y 0 0 1 0 0 1 m[110] m[110] 0 -1 0 X 0 1 0 0 y 0 0 0 1
对称心(i),反演 x’ y’ z’ x y z -1 -0 -0 -0 -1 -0 -0 -0 -1 = m[001] x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 m[100] x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 m[010] x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 m[110] x’ y’ z’ x y z = -0 -1 -0 -1 -0 -0 -0 -0 -1 m[110] x’ y’ z’ x y z = -0 -1 -0 -1 -0 -0 -0 -0 -1 镜面
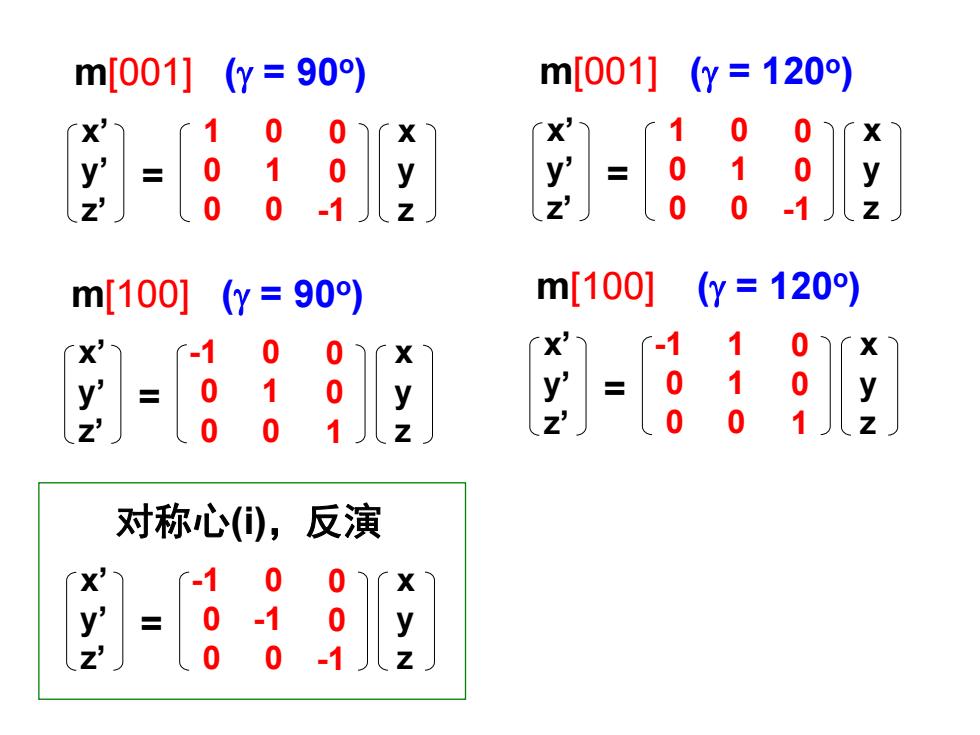
m[001](y=90) m[001] (y=120) 0 0 1 0 0 1 1 0 0 1 0 1 m[100](y=90) m[100](y=120) -1 0 对称心), 反演 0 0 .1
m[001] ( = 90o) x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 m[001] ( = 120o) x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 对称心(i),反演 x’ y’ z’ x y z -1 -0 -0 -0 -1 -0 -0 -0 -1 = m[100] ( = 90o) x’ y’ z’ x y z = -1 -0 -0 -0 -1 -0 -0 -0 -1 m[100] ( = 120o) x’ y’ z’ x y z = -1 -0 -0 -1 -1 -0 -0 -0 -1