
七种晶系 对称条件 晶系 特点 1(E)或1) 三斜 a≠b≠C,a+B≠y 2(c2)或2(m) 单斜 a+b≠c,=B=900+y 两个2(c2)或2(m) 正交 a+b≠c,x=B=y=900 4(C4或4(S4) 四方 a=b≠c,a=B=y=900 3(C3)或3S65) 三方 a=b≠C,ax=B=90,y=120° M=b=C,=B=Y菱形 6(C6)或6(S35) 六方 a=b≠C,ax=B=90,y=120 四个三次轴 立方 a=b=G,a=B=y=90°
七种晶系 对称条件 晶系 特点 四个三次轴 三 斜 单 斜 正 交 四 方 三 方 六 方 立 方 1(E)或1(i) 2(C2 )或2(m) 两个2(C2 )或2(m) 4(C4 )或4(S4 3 ) 3(C3 )或3(S6 5 ) 6(C6 )或6(S3 5 ) a ≠ b ≠ c, ≠ ≠ a ≠ b ≠ c, = = 90o ≠ a ≠ b ≠ c, = = = 90o a = b ≠ c, = = = 90o a = b ≠ c, = = 90o , = 120o a = b = c, = = = 90o a = b = c, = = 菱形 a = b ≠ c, = = 90o , = 120o

晶体的对称性 对称性:指该物体(或图形)是出两个或两个以上的部分组成,借助 某些辅助性的、假想的儿何要素(点、线、面)变换一下(线性变换) ,各部分调换位置之后整个物体(或图形)保持不变的性质,是品体的 基本性质之一: 若十个相问部分→对称元素>变换 →重合复原 对称元素:假想的儿何要素(点、线、面),分为宏观对称元素和微 观对称元素 旋转 对称
晶体的对称性

晶体的对称性 宏观对称元素: 由于晶体中的某部分为有限的几何图形, 具有点对称性 宏观对称元素。 对称中心i 反演 反映面 17m 反映 M 旋转轴n 旋转 L(a) 反轴n 旋转反演L(a1 微观对称元素:由于晶体的周期性结构,是无限的几何图 形,具有微观对称性 微观对称元素。 点阵 平移 T 螺旋轴nm 螺旋旋转 T(1)L(a) 由于微观对称操作中的平移量是极其微小的,宏观 观察时根本不可能分辨出来.所以,螺旋轴和滑移面 在宏观对称性中也会分别”退化”为旋转轴和镜面
晶体的对称性

晶体对称的特点:晶体外形的对称性(宏观对称 性)决定于晶体内部结构的对称性(微观对称性)。所有的晶 体结构都是对称的。晶体外形是有限图形,宏观对称是有限的, 而微观对称被视作无限的。晶体的对称不仅体现在外形上,同 时也体现在物理性质上。 我们必须记住:对于晶体结构,所讨论的是单胞连同其中所含 实体的对称性,而不是阵点排成的裸单胞的对称性 重要概念:对称操作、点对称操作、对称元素、参考轴、 对称操作算符、真旋转、非真旋转、操作符号 点对称操作: 恒等,旋转轴,对称中心,镜面, 映轴,反轴
重要概念:对称操作、点对称操作、对称元素、参考轴、 对称操作算符、真旋转、非真旋转、操作符号 晶体对称的特点:晶体外形的对称性(宏观对称 性)决定于晶体内部结构的对称性(微观对称性)。所有的晶 体结构都是对称的。晶体外形是有限图形,宏观对称是有限的, 而微观对称被视作无限的。晶体的对称不仅体现在外形上,同 时也体现在物理性质上。 我们必须记住:对于晶体结构,所讨论的是单胞连同其中所含 实体的对称性,而不是阵点排成的裸单胞的对称性 点对称操作: 恒等,旋转轴,对称中心,镜面, 映轴,反轴
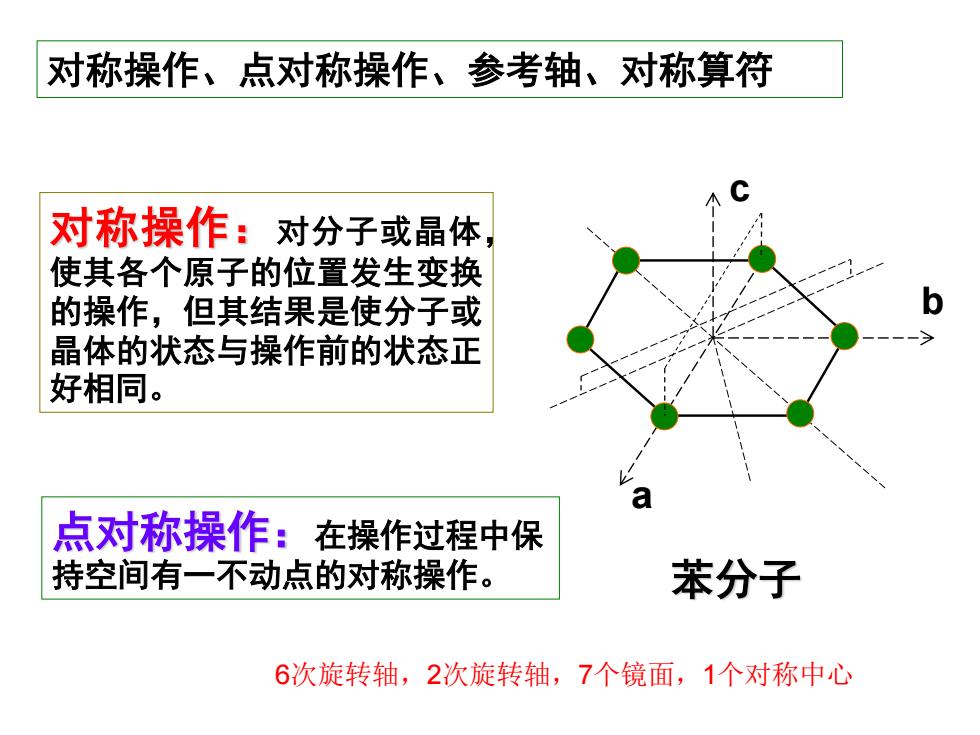
对称操作、点对称操作、参考轴、对称算符 对称操作:对分子或晶体 使其各个原子的位置发生变换 的操作,但其结果是使分子或 晶体的状态与操作前的状态正 好相同。 点对称操作:在操作过程中保 持空间有一不动点的对称操作。 苯分子 6次旋转轴,2次旋转轴,7个镜面,1个对称中心
对称操作、点对称操作、参考轴、对称算符 对称操作:对分子或晶体, 使其各个原子的位置发生变换 的操作,但其结果是使分子或 晶体的状态与操作前的状态正 好相同。 点对称操作:在操作过程中保 持空间有一不动点的对称操作。 苯分子 b a c 6次旋转轴,2次旋转轴,7个镜面,1个对称中心