
(二)正态分布的性质 (1)若X服从正态分布,则对任意的常数a(a0)、b,Z=aX+b也服 从正态分布。 (2)若X、Y服从正态分布,则对任意的常数a,b(a、b不全为0), Z=aX+bY也服从正态分布。 (3)若X1,X2,.,X,服从正态分布,且相互独立,则对任意n个常 数a1,42,.,an(不全为0),Za1X+a2X++anXn也服从正 态分布。 6
(二)正态分布的性质 (1)若X 服从正态分布,则对任意的常数 a( a ≠0)、b,Z=aX+b也服 从正态分布。 (2)若X 、Y服从正态分布,则对任意的常数 a、b( a 、b不全为0), Z=aX+bY也服从正态分布。 (3)若X 1, X 2,., X n服从正态分布,且相互独立,则对任意n个常 数 a1, a2 ,., an ( 不全为0),Z= a1 X1+ a2 X2+.+ an Xn也服从正 态分布。 6

(三)正态分布的数学期望和方差 X)- -(x-4)2 =(,4Xg+u=a v(X)=x2f(x)dx-u -(x-42 e 202 dx-u2=o2 在正态分布中,数学期望值和方差σ2分别为位置参数和形状参数,记 为X≈N(u,σ2)
(三)正态分布的数学期望和方差 e d x x E X xf x d x x e d x x x 2 1 2 ( ) 2 2 2 1 ( ) ( ) 2 2 2 2 2 2 2 2 2 1 x e dx V( X ) x f ( x )dx ( x ) 在正态分布中,数学期望值μ和方差σ 2分别为位置参数和形状参数,记 为X~N(μ, σ 2 ) 7
(四)标准正态分布 标准正态分布:X~N(0,1) p (x) =0=1 -x δ 标准正态分布概率密度函数0(x): 由于对称性、面积为1p(一x)=1一9(x)
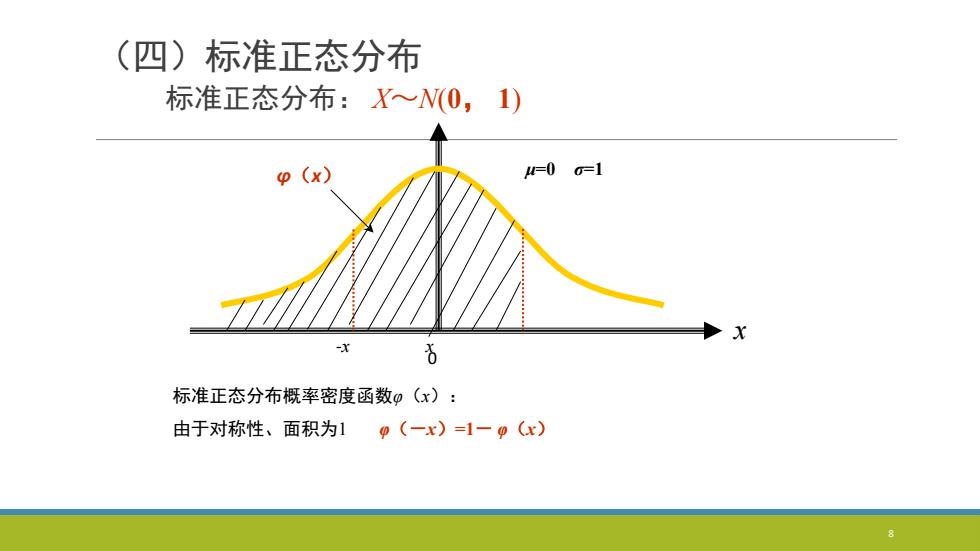
(四)标准正态分布 标准正态分布: X~N(0, 1) 标准正态分布概率密度函数φ(x): 由于对称性、面积为1 φ(-x)=1- φ(x) 0 x μ=0 σ=1 -x x φ(x) 8

(五)一般正态分布的标准化 由正态分布的性质1可知,X~N(4,σ2),则(X一)1o也 服从正态分布。 令Z=(Xμ)1o E2=。(X-0=2E(X0-川=(u-川=0 va=vK-=vK-0=2.2=1
(五)一般正态分布的标准化 由正态分布的性质1可知,X ~N(μ, σ 2 ),则(X-μ)/σ也 服从正态分布。 令Z= (X-μ)/σ 0 1 ( ) 1 ( ) 1 ( ) E Z E X E X 1 1 V( ) 1 V( ) 1 V( ) 2 2 2 2 Z X X 9

Z服从均值为0,方差为1的标准正态分布,即Z~N(0,1) 于是X的分布函数 PX=后z=1- 这种将变量线性变换为☑变量的过程,称为正态分布标准化。经 过标准化,对任意x,通过查标准正态分布表求得的0(z)函数值。 0
于是X的分布函数 这种将X变量线性变换为Z变量的过程,称为正态分布标准化。经 过标准化,对任意x,通过查标准正态分布表求得的φ(z)函数值。 Z服从均值为0,方差为1的标准正态分布,即Z ~N(0, 1 ) x x P Z X x P X x P x x P Z X x P X x P ( ) ( ) 1 ( ) ( ) 10