
10.2.3希尔排序 基本思想 先将整个待排序的记录序列分割为若干个子序列并 分别进行直接插入排序,待整个序列中的记录基本有 序时,再对全体记录进行一次直接插入排序。 基本步骤 在直接插入排序中,当n较小时,排序的效率比较高。 Shell将待排序的记录按照距离d(增量)分成若干个组, 把所有下标值相差d倍数的记录放在一组,然后在各组 内进行直接插入排序。 然后改变d的值,使其逐步缩小,各组内的记录逐渐 增多。各组的记录随着d的变小而趋向有序。因而重新 分组后,排序速度较快。当增量减小到1时,已达到基 本有序,最后再进行直接插入排序
10.2.3 希尔排序 ◼ 基本思想 先将整个待排序的记录序列分割为若干个子序列并 分别进行直接插入排序,待整个序列中的记录基本有 序时,再对全体记录进行一次直接插入排序。 ◼ 基本步骤 在直接插入排序中,当n较小时,排序的效率比较高。 Shell将待排序的记录按照距离d(增量)分成若干个组, 把所有下标值相差d倍数的记录放在一组,然后在各组 内进行直接插入排序。 然后改变d的值,使其逐步缩小,各组内的记录逐渐 增多。各组的记录随着d的变小而趋向有序。因而重新 分组后,排序速度较快。当增量减小到1时,已达到基 本有序,最后再进行直接插入排序
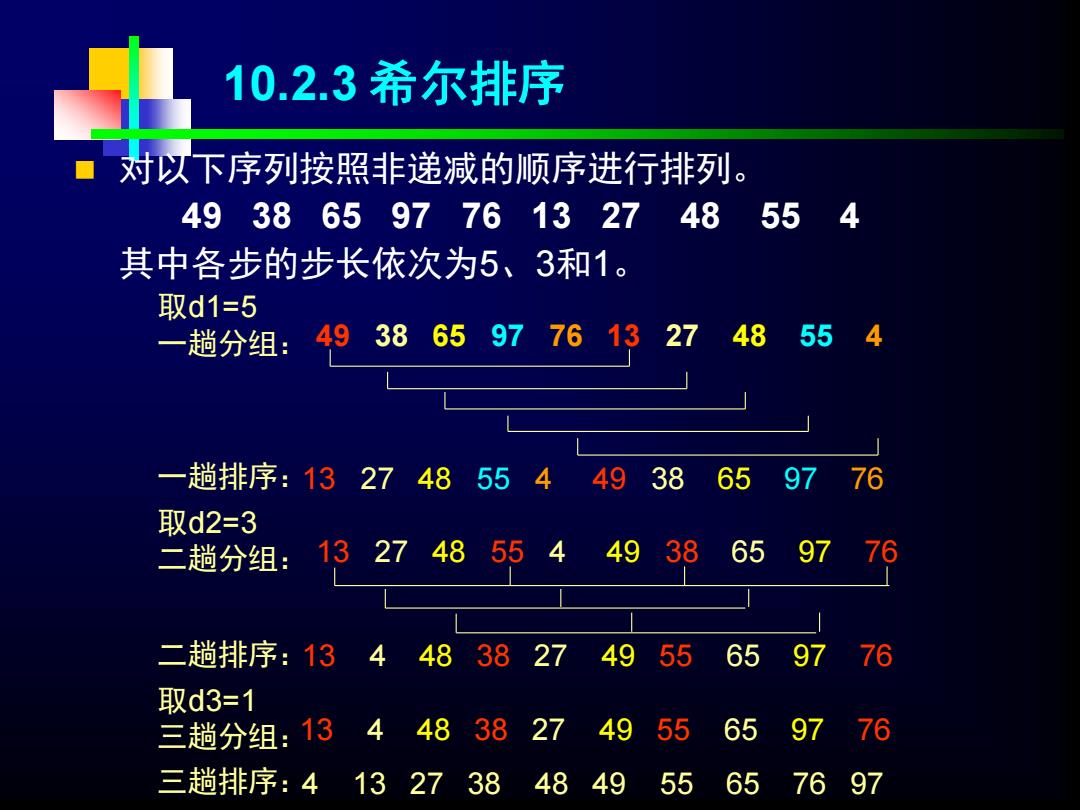
10.2.3希尔排序 对以下序列按照非递减的顺序进行排列。 4938659776132748 554 其中各步的步长依次为5、3和1。 取d1=5 一趟分组: 4938659776132748554 趟排序:13274855 4 4938659776 取d2=3 二趟分组: 1327485544938659776 二趟排序:13 4 4838274955659776 取d3=1 三趟分组:13 44838274955 659776 三趟排序:4132738484955657697
◼ 对以下序列按照非递减的顺序进行排列。 49 38 65 97 76 13 27 48 55 4 其中各步的步长依次为5、3和1。 取d3=1 三趟分组:13 4 48 38 27 49 55 65 97 76 三趟排序:4 13 27 38 48 49 55 65 76 97 一趟排序:13 27 48 55 4 49 38 65 97 76 二趟排序:13 4 48 38 27 49 55 65 97 76 取d1=5 一趟分组: 49 38 65 97 76 13 27 48 55 4 取d2=3 二趟分组: 13 27 48 55 4 49 38 65 97 76 10.2.3 希尔排序

void InsertSort(SqList &L){ for(i=2;i<=L.length;++i) if(L.R[i].key<L.R[i-1].key){ ∥<需将L[插入有序表 L.R[O]=L.R[i]; /复制为哨兵 for(j=i-1;L.R[O].key<L.R[j].key;--j) L.R[j+1]=L.R[j] /记录后移 L.R[j+1]=L.R[0]: 插入到正确位置 void ShellInsert(SqList &L,int dk) for (i=dk+1;i<=L.length;++i) if(L.R[i].key<L.R[i-dk].key) L.r[0]=L.r[i] ,/体从序列的第2个记录开始插入*/ for(j=i-dk;(j>0)&&(L.r[0].key<L.r[j].key);j-=dk) L.r[j+dk]=L.r[j]; /*记录后移找插入位置* L.r[j+dk]=Lr[O];/*插入L.[时*/
10.2.3 希尔排序 ◼ 希尔排序算法: void ShellSort(SqList &L,int d[],int t){ for(k=0;k<t;++k) ShellInsert(L, d[k]); /* 一趟增量为d[k]的插入排序*/ } void ShellInsert(SqList &L,int dk){ for (i=dk+1;i<=L.length;++i) if(L.R[i].key<L.R[i-dk].key){ L.r[0]=L.r[i]; /* 从序列的第2个记录开始插入*/ for(j=i-dk;(j>0)&&(L.r[0].key<L.r[j].key);j-=dk) L.r[j+dk]=L.r[j]; /* 记录后移找插入位置*/ L.r[j+dk]=L.r[0]; /* 插入L.r[i]*/ } } void InsertSort(SqList &L){ for(i=2;i<=L.length;++i) if(L.R[i].key<L.R[i-1].key){ //<需将L.r[i]插入有序表 L.R[0]=L.R[i]; //复制为哨兵 for(j=i-1;L.R[0].key<L.R[j].key;--j) L.R[j+1] = L.R[j]; //记录后移 L.R[j+1] = L.R[0]; //插入到正确位置 } }

10.2.3希尔排序 算法分析 时间复杂度 希尔排序算法的速度是所取的增量序列d的函数。增量 序列的选取是一件困难的事。一般认为, 希尔排序的 时间复杂度为O(nlog2n)。 空间复杂度 空间复杂度为0(1)。 稳定性 由于shel排序是分组进行排序,它是跳跃式向前移动, 会导致相等关键字中原来在后面的关键字移到前面, 所以希尔排序是不稳定的排序方法
◼ 算法分析 ❖ 时间复杂度 希尔排序算法的速度是所取的增量序列di的函数。增量 序列的选取是一件困难的事。一般认为,希尔排序的 时间复杂度为O(nlog2n)。 ❖ 空间复杂度 空间复杂度为O(1)。 ❖ 稳定性 由于shell排序是分组进行排序,它是跳跃式向前移动, 会导致相等关键字中原来在后面的关键字移到前面, 所以希尔排序是不稳定的排序方法。 10.2.3 希尔排序

10.3交换排序 10.3.1起泡排序 基本思想:首先将第一个记录的关键字和第二个记录的关键字 进行比较,若为逆序,则将两个记录交换之,然后比较第二个 记录和第三个记录的关键字。依次类推,直至第-1个记录和第 个记录的关键字进行过比较为止。上述过程称作第一趟起泡 排序,其结果使得关键字最大的记录被安置到最后一个记录的 位置上。然后进行第二趟起泡排序,对前-1个记录进行同样操 作,其结果使得关键字次大的记录被安置到第-1个记录的位置 上。第趟起泡排序是从L.r[1]到L.r[n-i+1]依次比较相邻两个记 录的关键字,并在逆序时交换到第-i+的位置上。判别起泡排 序结束条件是:在一趟排序过程中没有进行过交换记录的操作
10.3 交换排序 10.3.1 起泡排序 基本思想:首先将第一个记录的关键字和第二个记录的关键字 进行比较,若为逆序,则将两个记录交换之,然后比较第二个 记录和第三个记录的关键字。依次类推,直至第n-1个记录和第 n个记录的关键字进行过比较为止。上述过程称作第一趟起泡 排序,其结果使得关键字最大的记录被安置到最后一个记录的 位置上。然后进行第二趟起泡排序,对前n-1个记录进行同样操 作,其结果使得关键字次大的记录被安置到第n-1个记录的位置 上。第i趟起泡排序是从L.r[1]到L.r[n-i+1]依次比较相邻两个记 录的关键字,并在逆序时交换到第n-i+1的位置上。判别起泡排 序结束条件是:在一趟排序过程中没有进行过交换记录的操作