
Leaf Nodes in B+-Trees Properties of a leaf node: For i=1,2,...n-1,pointer P points to a file record with search-key value Ki ■ If Li,L;are leaf nodes and i<j,Lis search-key values are less than or equal to Lis search-key values P,points to next leaf node in search-key order leaf node Brandt Califieri Crick- Pointer to next leaf node 10101 Srinivasan Comp.Sci. 65000 12121 Wū Finance 90000 15151 Mozart Music 40000 22222 Einstein Physics 95000 32343 El Said History 80000 33456 Gold Physics 87000 45565 Katz Comp.Sci. 75000 58583 Califieri History 60000 76543 Singh Finance 80000 76766 Crick Biology 72000 83821 Brandt Comp.Sci. 92000 98345 Kim Elec.Eng. 80000 Database System Concepts-7th Edition 14.21 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 14.21 ©Silberschatz, Korth and Sudarshan th Edition Leaf Nodes in B+ -Trees ▪ For i = 1, 2, . . ., n–1, pointer Pi points to a file record with search-key value Ki , ▪ If Li , Lj are leaf nodes and i < j, Li’s search-key values are less than or equal to Lj’s search-key values ▪ Pn points to next leaf node in search-key order Properties of a leaf node:

Non-Leaf Nodes in B*-Trees Non leaf nodes form a multi-level sparse index on the leaf nodes.For a non-leaf node with m pointers: All the search-keys in the subtree to which Pi points are less than K1 ·For2≤i≤n-1,all the search-keys in the subtree to which F,points have values greater than or equal to K1 and less than K; All the search-keys in the subtree to which P points have values greater than or equal to K-1 General structure P1 K1 P2 Pn-1 Kn-1 Pn Database System Concepts-7th Edition 14.22 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 14.22 ©Silberschatz, Korth and Sudarshan th Edition Non-Leaf Nodes in B+ -Trees ▪ Non leaf nodes form a multi-level sparse index on the leaf nodes. For a non-leaf node with m pointers: • All the search-keys in the subtree to which P1 points are less than K1 • For 2 i n – 1, all the search-keys in the subtree to which Pi points have values greater than or equal to Ki–1 and less than Ki • All the search-keys in the subtree to which Pn points have values greater than or equal to Kn–1 • General structure
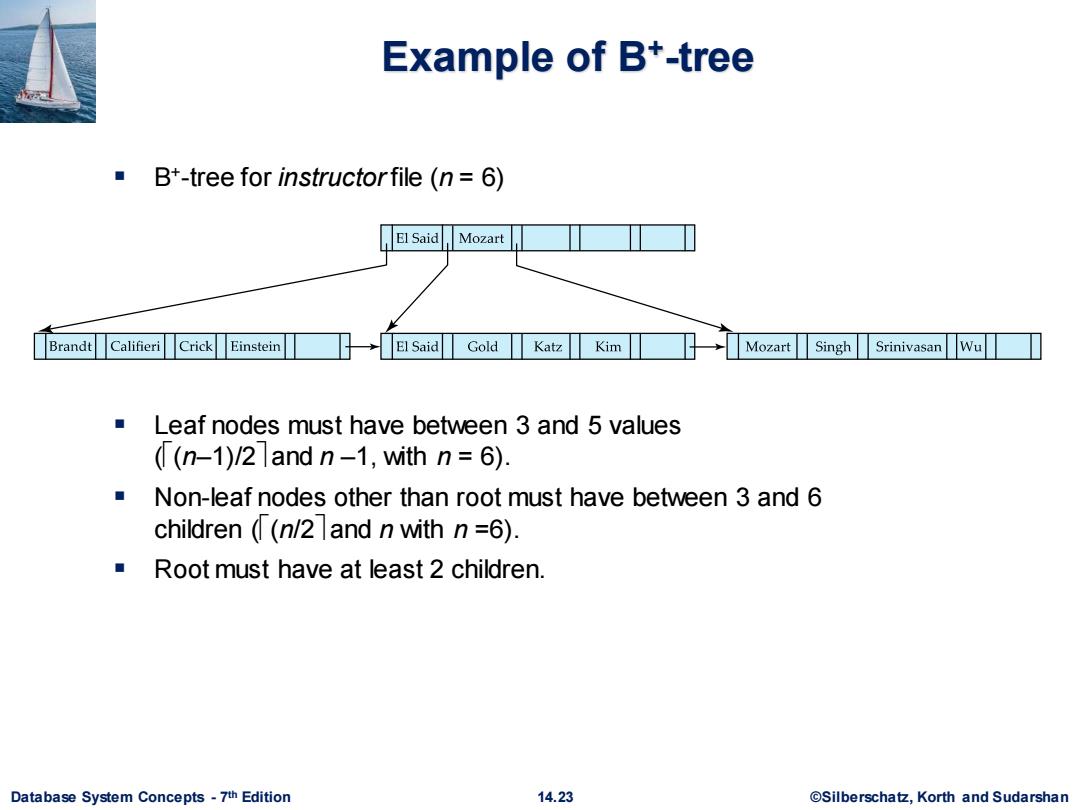
Example of B*-tree B+-tree for instructorfile (n=6) El Said Mozart Brandt Califieri Crick Einstein El Said Gold Katz Kim Mozart Singh SrinivasanWu Leaf nodes must have between 3 and 5 values (n-1)/2and n-1,with n 6) Non-leaf nodes other than root must have between 3 and 6 children ((n/2 and n with n =6). Root must have at least 2 children. Database System Concepts-7th Edition 14.23 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 14.23 ©Silberschatz, Korth and Sudarshan th Edition Example of B+ -tree ▪ B+ -tree for instructor file (n = 6) ▪ Leaf nodes must have between 3 and 5 values ((n–1)/2 and n –1, with n = 6). ▪ Non-leaf nodes other than root must have between 3 and 6 children ((n/2 and n with n =6). ▪ Root must have at least 2 children

Observations about B*-trees Since the inter-node connections are done by pointers,"logically"close blocks need not be“physically”close. The non-leaf levels of the B+-tree form a hierarchy of sparse indices. The B+-tree contains a relatively small number of levels Level below root has at least 2*n/2 values ■Next level has at least2*[n/2*「n/2 values .etc. If there are K search-key values in the file,the tree height is no more than logrnt21(K) thus searches can be conducted efficiently ■ Insertions and deletions to the main file can be handled efficiently,as the index can be restructured in logarithmic time (as we shall see). Database System Concepts-7th Edition 14.24 ©Silberscha乜,Korth and Sudarshan
Database System Concepts - 7 14.24 ©Silberschatz, Korth and Sudarshan th Edition Observations about B+ -trees ▪ Since the inter-node connections are done by pointers, “logically” close blocks need not be “physically” close. ▪ The non-leaf levels of the B+ -tree form a hierarchy of sparse indices. ▪ The B+ -tree contains a relatively small number of levels ▪ Level below root has at least 2* n/2 values ▪ Next level has at least 2* n/2 * n/2 values ▪ .. etc. • If there are K search-key values in the file, the tree height is no more than logn/2 (K) • thus searches can be conducted efficiently. ▪ Insertions and deletions to the main file can be handled efficiently, as the index can be restructured in logarithmic time (as we shall see)
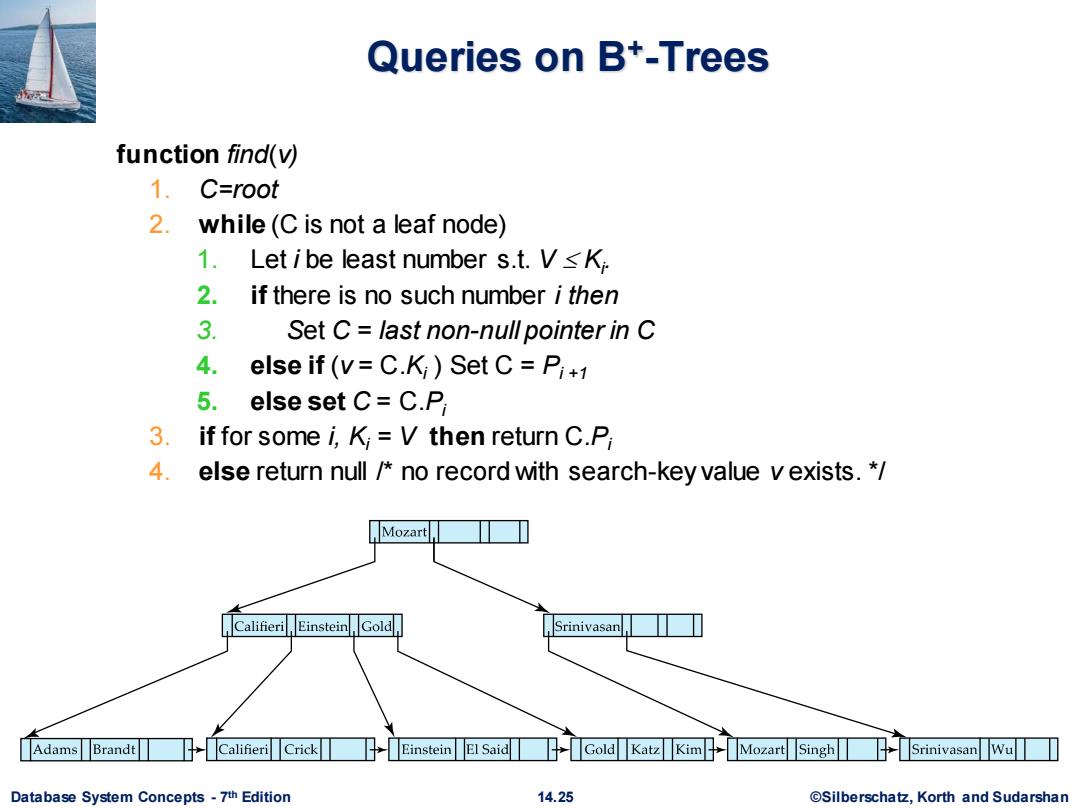
Queries on B+-Trees function find(v) 1.C=root 2.while(C is not a leaf node) 1.Let ibe least number s.t.V<K 2.if there is no such number i then 3. Set C=last non-null pointer in C 4. else if(v=C.K)Set C=P+1 5.else set C=C.P 3. if for some i,K=V then return C.P 4. else return null /no record with search-key value v exists.* Mozart Califieri,Einstein,Gold Srinivasan AdamsBrandt Califieri Crick Einstein El Said Gold Katz Kim MozartSingh SrinivasanWu Database System Concepts -7th Edition 14.25 @Silberschatz,Korth and Sudarshan
Database System Concepts - 7 14.25 ©Silberschatz, Korth and Sudarshan th Edition Queries on B+ -Trees function find(v) 1. C=root 2. while (C is not a leaf node) 1. Let i be least number s.t. V Ki . 2. if there is no such number i then 3. Set C = last non-null pointer in C 4. else if (v = C.Ki ) Set C = Pi +1 5. else set C = C.Pi 3. if for some i, Ki = V then return C.Pi 4. else return null /* no record with search-key value v exists. */