
2.卡诺定理的两个重要推论: (1)在T,和T,两热源间工作的所有可逆 热机,其热机效率必相等,与工作物 质或变化的各类无关。 普遍遵循:可逆热机效率关系式 n=-W/Q1=(T1-T2)/T Q=W=2Q;=Q1+Q2 得: Q1/T1+Q2/T20
21 2. 卡诺定理的两个重要推论: (1) 在T1和T2两热源间工作的所有可逆 热机,其热机效率必相等,与工作物 质或变化的各类无关。 普遍遵循:可逆热机效率关系式 得: Q1 /T1+ Q2 /T2=0 = -W/Q1 = (T1 -T2 )/T1 Q = W = Qi = Q1+ Q2

(2)不可逆机的热机效率小于可逆机的热 机效率。 n<nR 将(1)和(2)两推论结合,得:nn取 因n=-W/Q,=(Q1+Q2)/Q MR=(TI-T2)/T n=-W/Q1=(Q1+Q2)/Q1≤(T1-T2)/T Q/T+Q2/T2≤0 不可逆 可逆
22 (2) 不可逆机的热机效率小于可逆机的热 机效率。 ηI<ηR 将(1)和(2)两推论结合,得:η≤ηR 因 = -W/Q1 = (Q1+ Q2 )/Q1 ηR = (T1 -T2 )/T1 = -W/Q1 = (Q1+ Q2 )/Q1 Q1 /T1+ Q2 /T2 ≤ 0 不可逆 可逆 ≤ (T1 -T2 )/T1

Q1/T1+Q2/T2≤0 不可逆 可逆 对微小过程 不可逆 òQ1/T+δQ2/T2≤0 可逆 3.可逆循环过程热温商 将卡诺循环的结果推广到任意的可 逆循环。 数学上可以证明同,任何可逆循环 均可划分成很多个无穷小的卡诺循环
23 Q1 /T1+ Q2 /T2 ≤ 0 不可逆 可逆 δQ1 /T1+ δQ2 /T2 ≤ 0 不可逆 可逆 对微小过程 3. 可逆循环过程热温商 将卡诺循环的结果推广到任意的可 逆循环。 数学上可以证明同,任何可逆循环 均可划分成很多个无穷小的卡诺循环
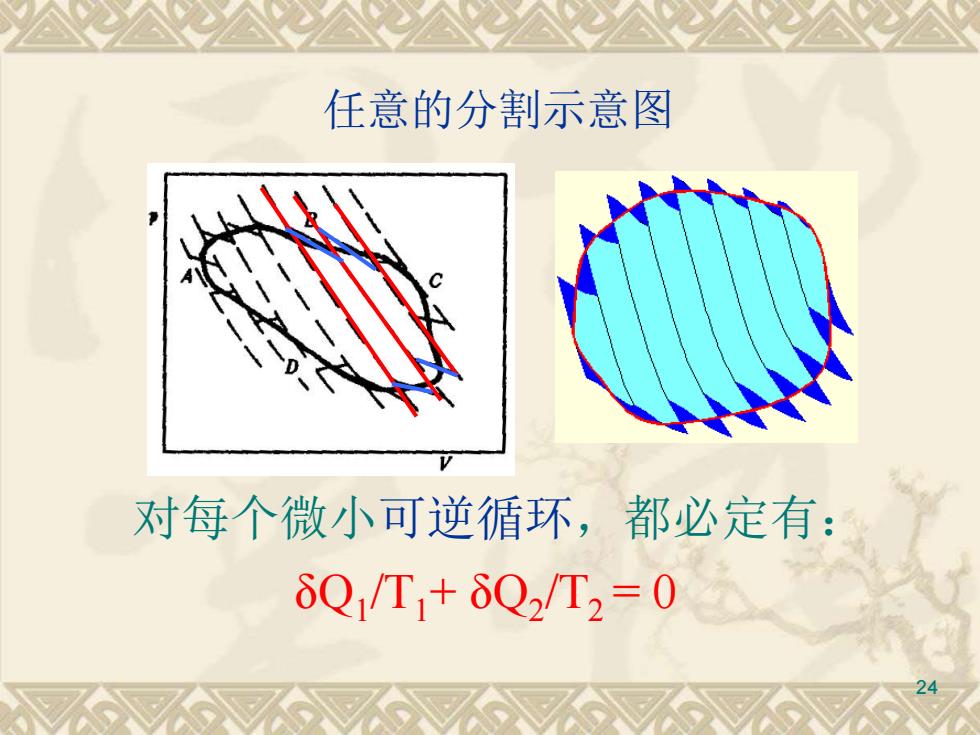
任意的分割示意图 对每个微小可逆循环,都必定有: òQ/T+6Q2/T2=0
24 任意的分割示意图 对每个微小可逆循环,都必定有: δQ1 /T1+ δQ2 /T2 = 0

将各微小可逆循环过程热温商之和相加 2(6Q1/T1+δQ2/T2)=0 2(6Qr/T:)=0 如果将各微小可逆循环过程分割成 无限小即极限情况,则有: $(6Q,/T)=0 根据全微分的充分必要条件 δQ,T必为单调、连续的状态函数
25 将各微小可逆循环过程热温商之和相加 (δQ1 /T1+ δQ2 /T2 ) = 0 (δQi,r /Ti ) = 0 如果将各微小可逆循环过程分割成 无限小即极限情况,则有: ∮(δQr / T ) = 0 根据全微分的充分必要条件 δQr /T必为单调、连续的状态函数