北京大学：《燃烧学基础》课程教学资源（讲义）基础燃烧理论课堂讲义（共七章，主讲：陈正）

基础燃烧理论义 陈正（比京大学工学院z@pku.edu.cn2014/120 2.2化学平衡 问题：封闭系统中在初始时刻有1 mole CO2,给定压力为P=10am,温度为 T=2500K。假设仅有可逆反应C0,一C0+0.502。问：化学平衡时封闭系统中 C02,C0和O2的摩尔数。 >热力学方程 单组分封闭系统：每个热力学状态量为其它两个状态量的函数。例如， E=E(S,门，P=nRT(n为摩尔数，R为气体常数) 多组分封闭系统：E=ES,V,),其中为m,组分i的摩尔数。组分种类数目为 N. -偿+袋内 TP一化学势= Gs自由能：G=H-,G=-T+P+交ua,4=品 >化学平衡条件 初态(0)：1 mole CO2,P=10atm,T=2500K 终态(t→，也称为平衡态)：？mole C02/C0/O2,P=10atm,T=2500K 约束条件：化学反应C02一C0+0.502达到平衡态，即熵最大/化学势最低 /Gibbs自由能最低。假设有CO2离解的百分数为a,即有amole CO2经反应生成 C0和02：C02(1-a)C02+cC0+0.5a02。(注：质量守恒和元素守恒自动 满足。)

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 9 2.2 化学平衡 问题：封闭系统中在初始时刻有 1 mole CO2，给定压力为 P=10 atm，温度为 T＝2500K。假设仅有可逆反应 2 O2 CO  CO  0.5 。问：化学平衡时封闭系统中 CO2，CO 和 O2 的摩尔数。  热力学方程 单组分封闭系统：每个热力学状态量为其它两个状态量的函数。例如， E=E(S,V)，P=nR0 T/V (n 为摩尔数，R0 为气体常数)。 多组分封闭系统：E=E(S,V,ni)，其中为 ni组分 i 的摩尔数。组分种类数目为 N。                  N i S V n i i V n S n dn n E dV V E dS S E dE i i i i j 1 , , , , ( ) ( ) ( ) ( ) V ni S E T , ( )    ， S ni V E P , ( )     ，化学势 ( ) , , ( )S V nj j i i i n E          N i dE TdS PdV i dni 1 ( ) 焓： H  E  PV ，     N i dH TdS VdP i dni 1 ( )， ( ) , , ( )S P nj j i i i n H      Gibbs 自由能：G  H  TS ，      N i dG SdT VdP i dni 1 ( )， ( ) , , ( )T P nj j i i i n G       化学平衡条件 初态(t=0)：1 mole CO2，P=10 atm，T＝2500K 终态(t→∞，也称为平衡态)：? mole CO2/CO/O2，P=10 atm，T＝2500K 约束条件：化学反应 2 O2 CO  CO  0.5 达到平衡态，即熵最大/化学势最低 /Gibbs 自由能最低。假设有 CO2 离解的百分数为 α，即有 α mole CO2 经反应生成 CO 和 O2： 2 2 O2 CO  (1 )CO  CO  0.5 。(注：质量守恒和元素守恒自动 满足。)

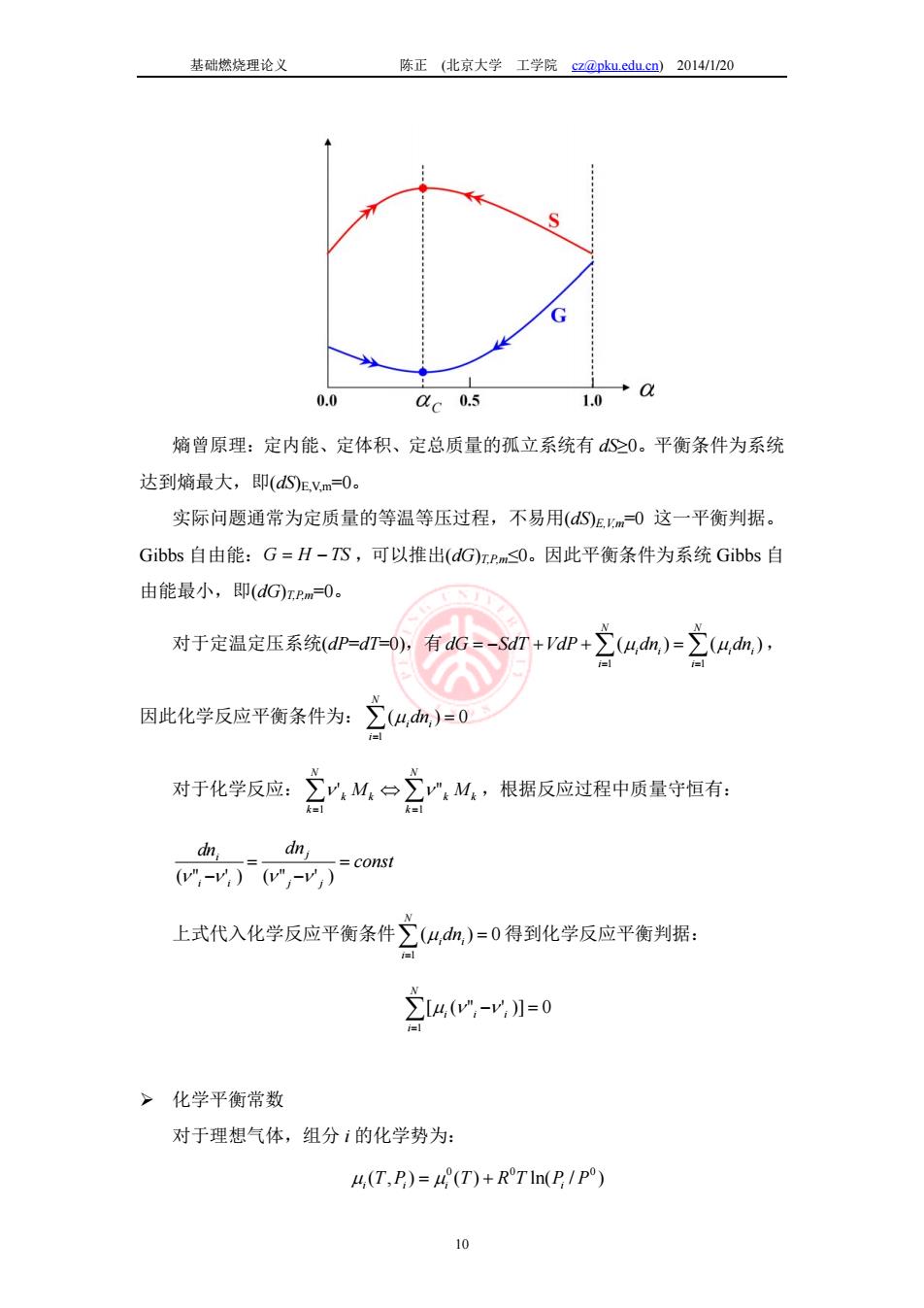
基础燃烧理论义 陈正（北京大学工学院z@pku.edu.cn)2014/120 0.0 ac0.5 1.0+a 熵曾原理：定内能、定体积、定总质量的孤立系统有0。平衡条件为系统 达到熵最大，即(dS)Evm-0。 实际问题通常为定质量的等温等压过程，不易用(dSEm0这一平衡判据。 Gibbs自由能：G=H-IS,可以推出(dG)rPm≤O。因此平衡条件为系统Gibbs自 由能最小，即(dG)zPm-0。 对于定温定压系统dP=aT=O.有dG=-SdT+aP+之4dM,)=之(4dM), 因此化学反应平衡条件为： 2=0 对于化学反应：产，从一产，从，根据反应过程中质量守恒有： dn, (-Ψ)(，-，) 上式代入化学反应平衡条件∑(u,dm,)=0得到化学反应平衡判据： 24e-川=0 化学平衡常数 对于理想气体，组分1的化学势为： (T,P)=(T)+RTIn(P/P) 公

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 10 熵曾原理：定内能、定体积、定总质量的孤立系统有 dS≥0。平衡条件为系统 达到熵最大，即(dS)E,V,m=0。 实际问题通常为定质量的等温等压过程，不易用(dS)E,V,m=0 这一平衡判据。 Gibbs 自由能：G  H  TS ，可以推出(dG)T,P,m≤0。因此平衡条件为系统 Gibbs 自 由能最小，即(dG)T,P,m=0。 对于定温定压系统(dP=dT=0)，有          N i i i N i dG SdT VdP i dni dn 1 1 ( ) ( )， 因此化学反应平衡条件为： ( ) 0 1    N i i dni 对于化学反应：     N k k k N k k Mk M 1 1  ' " ，根据反应过程中质量守恒有： const dn dn j j j i i i    ("  ' ) ("  ' ) 上式代入化学反应平衡条件 ( ) 0 1    N i i dni 得到化学反应平衡判据： [ ( " ' )] 0 1     N i i  i  i  化学平衡常数 对于理想气体，组分 i 的化学势为： ( , ) ( ) ln( / ) 0 0 0 i T Pi  i T  R T Pi P

基础燃烧理论义 陈正（比京大学工学院z@pku.edu.cm2014/120 其中a°为标准状态下(P=p=1aim)纯物质(P=P)的Gibbs自由能。 思考愿：利用上述定义以及G-立小，推导出化学平衡时即O 时，有∑(4，dm,)=0。 将化学势的定义代入化学反应平衡判据立4(-，小=0中，则有 eK.O=p心-yR7 其中K定义为化学（反应）平衡常数，它只是温度的函数，与压力无关。 给定压力P,由于P=xP,因此有： e).P）连 "=K(T)=exp-)(T(RT) 给定摩尔浓度C,由状态方程P,=C,RT,因此有： II(C)-k() RT-) =Kc(T) 其中K。为基于摩尔浓度的化学（反应）平衡常数。在，-V,)=0时有， Kp(T)=Kc(T). 思考题：同一温度下，反应C0+0.502-C02和反应2C0十02-=2C02的化学 反应的平衡常数分别为K1和KP2,请写出K,和K2之间的关系。 >例题 封闭系统中在初始时刻有1 mole CO2,给定压力为P=10am,温度为T= 2500K。假设仅有可逆反应C02一C0+0.502。问：化学平衡时封闭系统中C02 体积百分数xco2=? 解：查表得T=2500K时：48o2=-396152KJ1 Kmole, uco =-327245 KJ/Kmole,on =0 KJ/Kmole

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 11 其中 μi 0 为标准状态下(P=P0 =1 atm )纯物质(Pi=P)的 Gibbs 自由能。 思考题：利用上述定义以及   N i G i ni 1 ( ) ，推导出化学平衡时，即(dG)T,P,m=0 时，有 ( ) 0 1    N i i dni 。 将化学势的定义代入化学反应平衡判据 [ ( " ' )] 0 1     N i i  i  i 中，则有： ( ) exp{ [( " ' ) ( )]/( )} 0 1 0 ( " ' ) 0 1 K T T R T P P N i P i i i i N i i i                    其中 KP定义为化学(反应)平衡常数，它只是温度的函数，与压力无关。 给定压力 P，由于 Pi=xiP，因此有：   ( ) exp{ [( " ' ) ( )]/( )} 0 1 0 ( " ' ) 0 ( " ' ) 1 1 K T T R T P P x N i i P i i i N i N i i i i i                          给定摩尔浓度 Ci，由状态方程 Pi＝CiR0 T，因此有：   ( )/ ( ) 1 ( " ' ) 0 0 ( " ' ) 1 K T P R T Ci KP T C N i N i i i i i                     其中 KC 为基于摩尔浓度的化学(反应)平衡常数。在 ( " ' ) 0 1     N i  i  i 时有， K (T ) K (T ) P  C 。 思考题：同一温度下，反应 CO＋0.5O2=CO2 和反应 2CO＋O2=2CO2 的化学 反应的平衡常数分别为 KP1 和 KP2，请写出 KP1 和 KP2 之间的关系。  例题 封闭系统中在初始时刻有 1 mole CO2，给定压力为 P=10 atm，温度为 T＝ 2500K。假设仅有可逆反应 2 O2 CO  CO  0.5 。问：化学平衡时封闭系统中 CO2 体积百分数 xCO2=? 解：查表得 T ＝ 2500K 时 ： KJ Kmole CO 396152 / 0  2   ， KJ Kmole CO 327245 / 0    ， KJ Kmole O 0 / 0  2 

基础燃烧理论义 陈正（比京大学工学院z@pk.edu.cn)2014/1/20 对于反应C0,台C0+0.50,有 ((.o68097 KJ Kmole 因此有 K,(T)=ep-立w-)4T】RT)=exp-680978.315x2500 由化学平衡常数的定义以及反应定律P=x,P有 kn- 利用P=10atm和P=latm,有 x xco10 68097 Xco2 =exp(-8315x2500 根据体积百分数的归一性有 X02+xco+Xc02=1 第三个方程根据化学反应C02一C0+0.50,得到： Xco=2X02 联合上述三个方程可以解出：xco2=0.9096。 讨论： 随着压力升高，由于Kr是一常数，因此平衡态xCo2升高，即CO2离解变少。 随着温度升高，K升高，因此平衡态xCam降低，即CO2离解变多。 T1>T2 P

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 12 对于反应 2 O2 CO  CO  0.5 有 T KJ Kmole CO CO CO N i i i i [( " ' ) ( )] 0.5 68097 / 0 2 0 0 2 1 0              因此有 ( ) exp{ [( " ' ) ( )]/( )} exp[ 68097 /(8.315 2500)] 0 1 0        K T T R T N i P  i  i i 由化学平衡常数的定义以及反应定律 Pi=xiP 有 1/ 2 0 2 1/ 2 2 ( " ' ) 0 1 ( )                  P P x x x P P K T CO i O CO N i P  i  i 利用 P=10 atm 和 P0=1 atm，有 ) 8.315 2500 68097 exp( 10 2 1/ 2 2    CO O CO x x x 根据体积百分数的归一性有 xO2  xCO  xCO2  1 第三个方程根据化学反应 2 O2 CO  CO  0.5 得到： CO 2 O2 x  x 联合上述三个方程可以解出：xCO2=0.9096。 讨论： 随着压力升高，由于 KP是一常数，因此平衡态 xCO2 升高，即 CO2 离解变少。 随着温度升高，KP升高，因此平衡态 xCO2 降低，即 CO2 离解变多

基础燃烧理论义 陈正(d比京大学工学院2@pku.ecm)2014/120 >LeChatelier原理： 任何一个初始处于平衡态的系统，当温度或压力发生变化后，它将向最大限 度地减少该变化的方向去改变组分。当压力升高时，则平衡向产生更少的物质量 (摩尔数)的反应方向变化。对于反应C0,一C0+0.50,压力升高时则反应朝 C02生成的方向变化。对于等分子反应（∑("-，）=0)，压力没有影响。当温 度升高时，则平衡向吸热反应方向变化。由于C02离解为C0和O2是吸热反应， 因此升高温度会导致更多的C02发生离解。 化学平衡常数的应用：发动机燃烧室内取样，测得压力P以及H、O2、O、 OH的摩尔百分数，问燃烧室内温度T=?(利用化学平衡H+O,台O+OH) >相变平衡Ma一M 相变平衡条件为：。=凸 因此有：d4。=d4 由定义G=立)得：G-2u血+空 由于dG=-SdT+VdP+∑(u,dm,),因此有 立ng)=-ir+n 上述关系对气态和液态均适用，因此有 N dug =-S dT+V dP,dug =-s dT+vdP N du =-S,dT +V dp,du =-s dT+vdf 其中s=S/m,y=V1n 利用d4=d4则有： dP_5- dT vs-vi 13

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 13  Le Chatelier 原理： 任何一个初始处于平衡态的系统，当温度或压力发生变化后，它将向最大限 度地减少该变化的方向去改变组分。当压力升高时，则平衡向产生更少的物质量 (摩尔数)的反应方向变化。对于反应 2 O2 CO  CO  0.5 ，压力升高时则反应朝 CO2 生成的方向变化。对于等分子反应( 0 ( " ' ) 1     N i  i  i )，压力没有影响。当温 度升高时，则平衡向吸热反应方向变化。由于 CO2 离解为 CO 和 O2 是吸热反应， 因此升高温度会导致更多的 CO2 发生离解。 化学平衡常数的应用：发动机燃烧室内取样，测得压力 P 以及 H、O2、O、 OH 的摩尔百分数，问燃烧室内温度 T=? (利用化学平衡H  O2  O  OH )  相变平衡 Mgas  Mliquid 相变平衡条件为：g  l 因此有：dg  dl 由定义   N i G i ni 1 ( ) 得：       N i i i N i dG i dni n d 1 1 ( ) (  ) 由于      N i dG SdT VdP i dni 1 ( ) ，因此有 n d SdT VdP N i  i i    1 (  ) 上述关系对气态和液态均适用，因此有 Ngdg  SgdT VgdP ，即dg  sgdT  vgdP Nl dl  Sl dT Vl dP，即dl  sl dT  vl dP 其中 i Si ni s  / ， i i i v V / n 利用dg  dl 则有： g l g l v v s s dT dP   