
U K 由以前的结论,有: 2Na=qaD→ N= Ay D2 动应力 48 强度条件 ≤[o] 8 可看出:要保证圆环的强度,只能限制圆环的 转速,增大截面积4并不能提高圆环的强度
11 由以前的结论,有: 2Nd = qd D 2 d d q D N = 2 2 4 g A D = 动应力 A N d d = g D 4 2 2 = g v 2 = 强度条件 g v 2 d = [ ] 可看出:要保证圆环的强度,只能限制圆环的 转速,增大截面积A并不能提高圆环的强度
U K 例3(书例10.1) 已知:n=l00r/min, 转动惯量1=0.5 剩车离合器 kNms2。轴直径 d=100mm。刹车 时在10秒内均匀 7 减速停止转动。 求:轴内最大动应力。 解:角速度 nπ 10元 rad/s 30 3 角加速度8= 0-0- 元 rad/s2 3
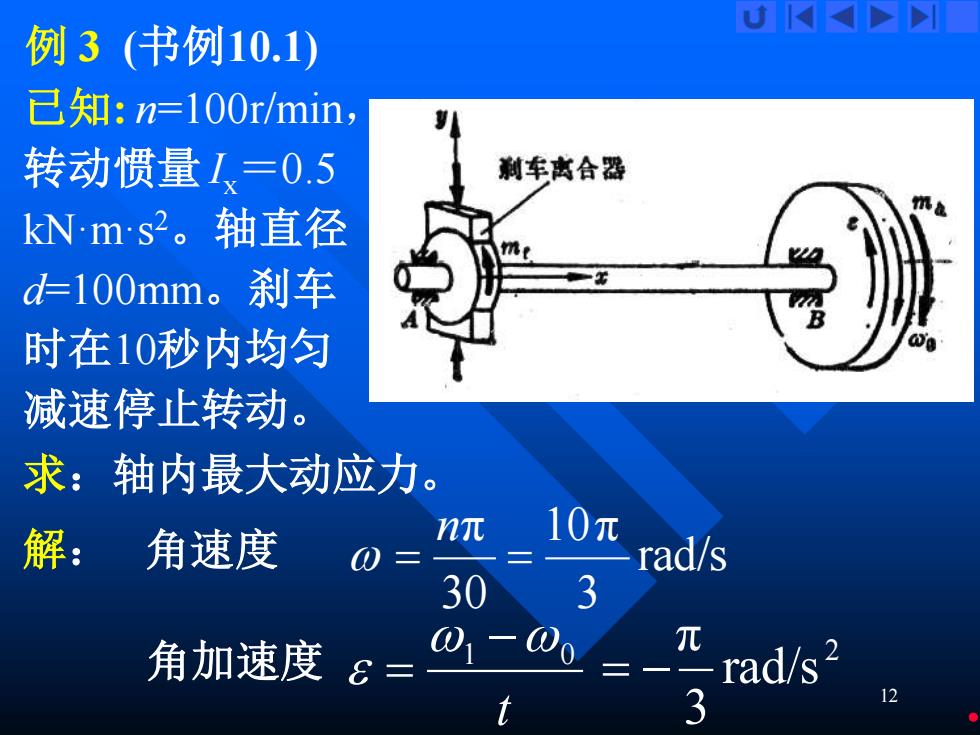
12 例 3 (书例10.1) 已知 : n=100r/min , 转动惯量 Ix =0.5 kN·m·s 2。轴直径 d=100mm。刹车 时在10秒内均匀 减速停止转动。 求:轴内最大动应力 。 解 : 角速度 30nπ = rad/s 3 10 π = 角加速度 t 1 0 − = 2 rad/s 3π = −