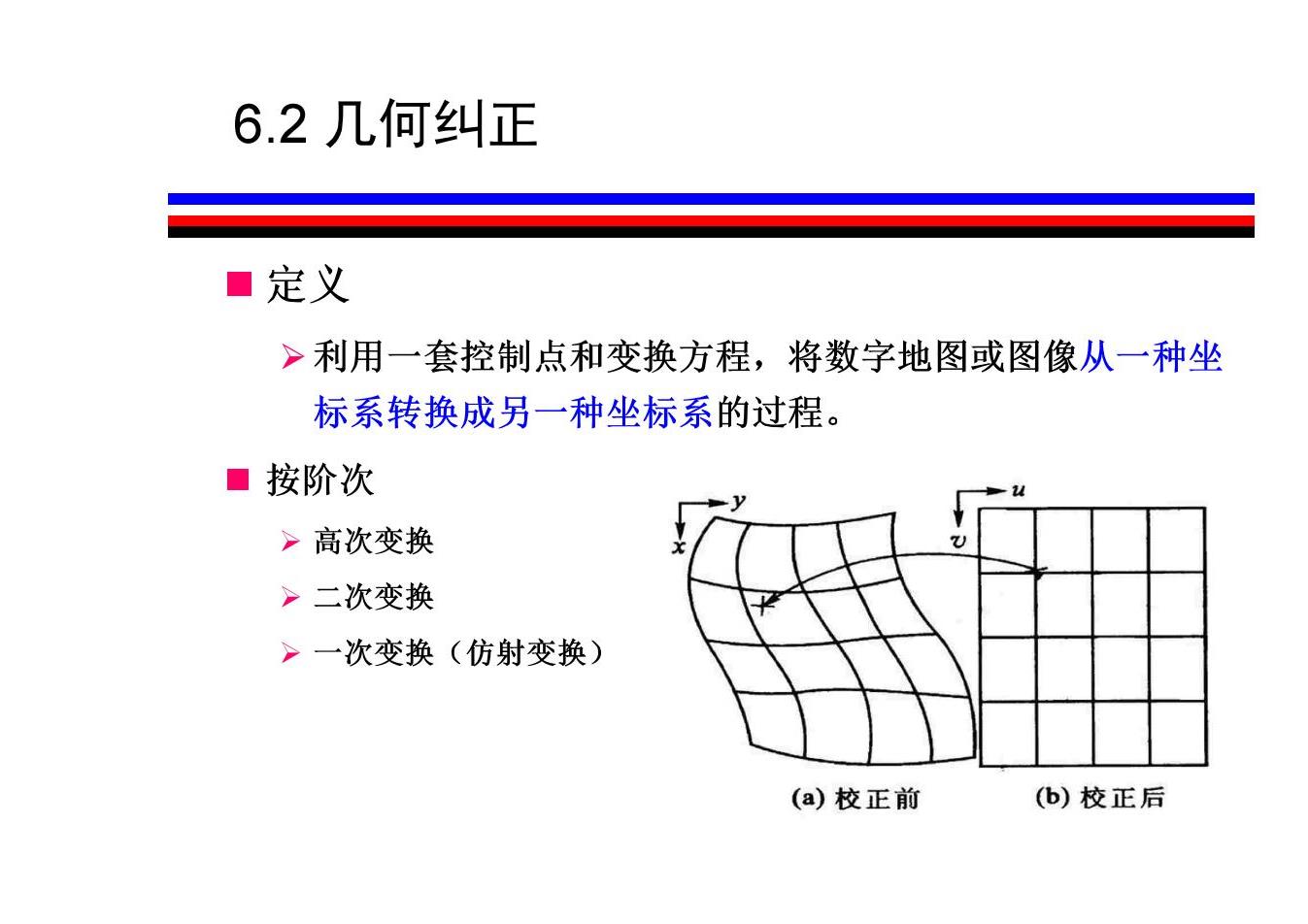
6.2几何纠正 ■定义 >利用一套控制点和变换方程,将数字地图或图像从一种坐 标系转换成另一种坐标系的过程。 ■按阶次 >高次变换 >二次变换 >一次变换(仿射变换) (a)校正前 (b)校正后

6.2几何纠正 1、高次变换 x'=ax+azy+anx2+arzxy azy2+A y'=bx+bay+bux2+baxy+baay2+B 其中A、B代表二次以上高次项之和。上式是高次曲线方程,符合 上式的变换称为高次变换。式中有12个未知数,所以在进行高次变 换时,需要有6对以上控制点的坐标和理论值,才能求出待定系数。 2、二次变换 当不考虑高次变换方程中的A和B时,则变成二次曲线方程,称 为二次变换。二次变换适用于原图有非线性变形的情况,至少需 要5对控制点的坐标及其理论值,才能解算待定系数

6.2几何纠正 3.一次变换 仿射变换的数学表达式为一次线性方程: x=2 cos(8-0)+a=(cos 8cos9-sin 8sin )+a y=22 sin(8-)+b=22 (sin 8cos0+cos 8sin 8)+b 即 x=Q(x1cos9-ylsin 8)+a y=22 (x1sin 0+y1cose)+b x=alx1+a2y1+a 简化为: y=B1x1+B2y1+B

6.2几何纠正 ■按变形 >等积变换:允许旋转矩形,保持形状与大小不变 >相似变换:允许旋转矩形,保持形状不变,但大小改 变 >仿射变换:G引S常用,允许矩形角度改变,保留线的平 行性 >投影变换:允许角度和长度变形 >拓扑变换:保持拓朴不变
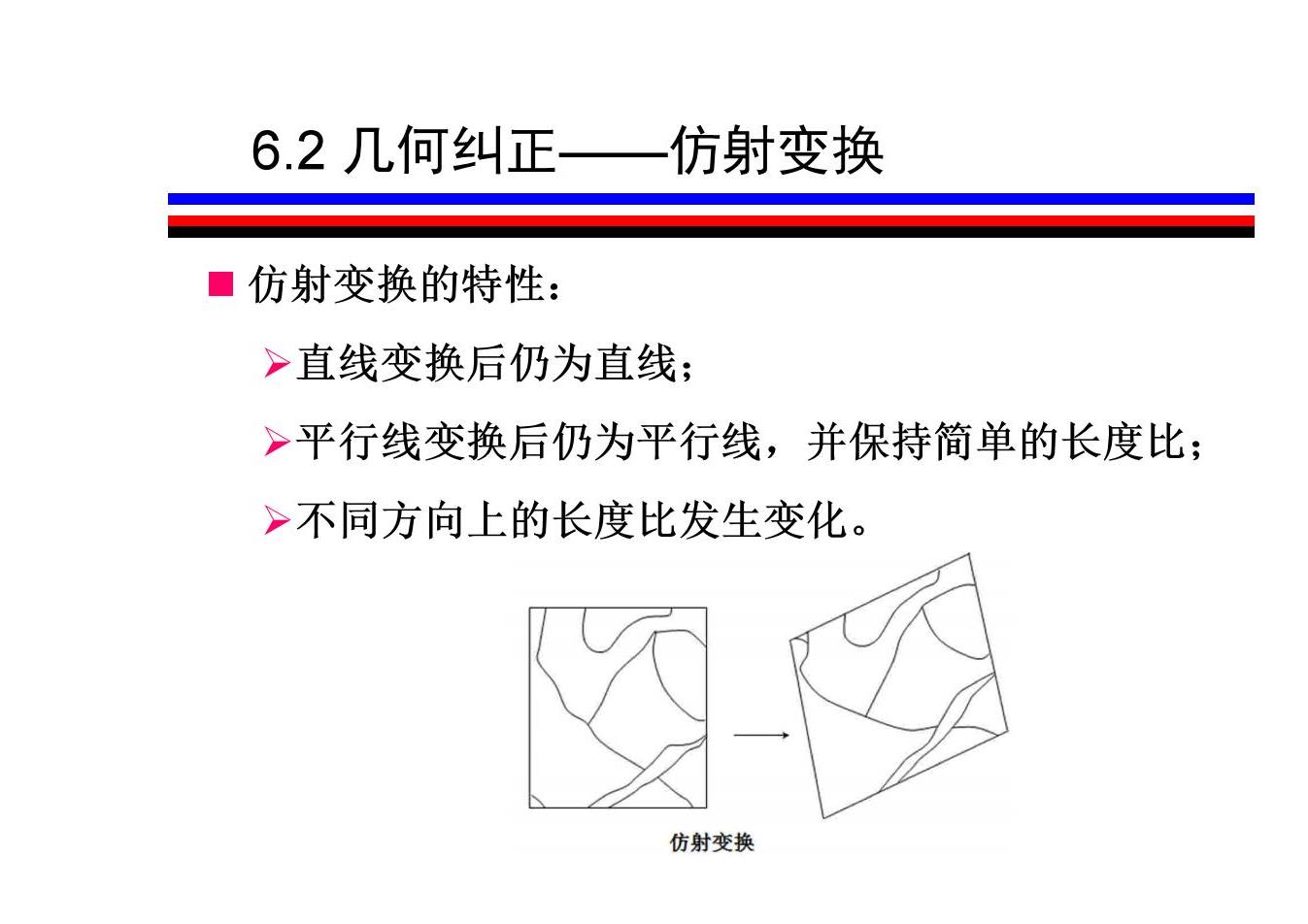
6.2几何纠正— 仿射变换 ■仿射变换的特性: >直线变换后仍为直线: >平行线变换后仍为平行线,并保持简单的长度比; >不同方向上的长度比发生变化。 仿射变换