《通信原理》课程教学资源（PPT课件讲稿）第5章 模拟调制系统

第5章模拟调制系统 将 Sysg(@)=Spsr(@).H(@)=]IM(@+@.)+Mo-@.)]H(@) 代入 S,(o)=[Ss(o+0.)+Ss(0-0.)] 得到 S,(@)-][M(@+2@.)+M@)H(@+0.) =2[M(o)+M(o-2@.】H(o-0.) 式中Mo+20)及Mo-20c)是搬移到+20和-20处的频谱， 它们可以由解调器中的低通滤波器滤除。于是，低通滤 波器的输出频谱为 S@)-zM(@[H(w+0)+H(o-0) 26

26 第5章 模拟调制系统 将 代入 得到 式中M( + 2c )及M( - 2c )是搬移到+ 2c和 -2c处的频谱， 它们可以由解调器中的低通滤波器滤除。于是，低通滤 波器的输出频谱为 S S S p VSB c VSB c (     ) = + + −  ( ) ( ) S S H VSB DSB ( )    =  ( ) ( ) 1 [ ( ) )] ( ) 2 = + + − M M H      c c ( ) 1 [ ( 2 ) )] ( ) 2 S M M H p c c       = + + + 1 [ ( ) ( 2 )] ( ) 2 = + − − M M H      c c   1 ( ) ( ) ( ) ( ) 2 d c c S M H H       = + + −

第5章模拟调制系统 S,(@)=2Mo[Ho+o.)+Ho-a.】 显然，为了保证相干解调的输出无失真地恢复调制信 号()，上式中的传递函数必须满足： H(o+0.)+H(o-o)=常数，回l≤0H 式中，⊙1·调制信号的截止角频率。 口上述条件的含义是：残留边带滤波器的特性H()在o处必 须具有互补对称（奇对称)特性，相干解调时才能无失真地 从残留边带信号中恢复所需的调制信号。 27

27 第5章 模拟调制系统 显然，为了保证相干解调的输出无失真地恢复调制信 号m(t)，上式中的传递函数必须满足： 式中，H － 调制信号的截止角频率。  上述条件的含义是：残留边带滤波器的特性H()在c处必 须具有互补对称（奇对称）特性, 相干解调时才能无失真地 从残留边带信号中恢复所需的调制信号。   1 ( ) ( ) ( ) ( ) 2 d c c S M H H       = + + − ( ) ( ) H H       + + − =  c c H 常数

第5章模拟调制系统 ▣残留边带滤波器特性的两种形式 ,残留“部分上边带”的滤波器特性：下图(a) ,残留“部分下边带”的滤波器特性：下图(b) ↑H(o) 1 0.5 (a) 0。 0 0.5 ⊙ (b 28

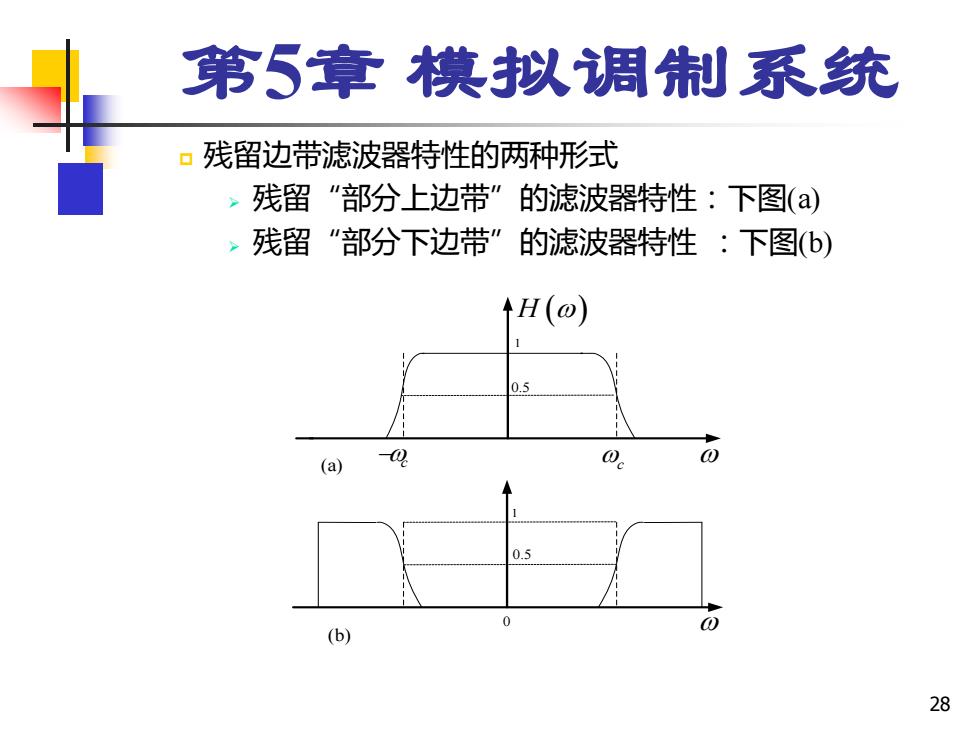
28 第5章 模拟调制系统  残留边带滤波器特性的两种形式 ➢ 残留“部分上边带”的滤波器特性：下图(a) ➢ 残留“部分下边带”的滤波器特性 ：下图(b) c 1 0.5H () −c   1 0.5 (a) (b) 0

第5章模拟调制系统 5.1.5线性调制的一般模型 ◆滤波法模型 在前几节的讨论基础上，可以归纳出滤波法线性调制 的一般模型如下： m0,☒ h(2) s cos@t 按照此模型得到的输出信号时域表示式为： s,(t)=[m(t)coso t]*h(t) 按照此模型得到的输出信号频域表示式为： S.(@)=-[M(@+@.)+M@-@.)]H(@) 式中， H(o)台h(t) 只要适当选择Hω)，便可以得到各种幅度调制信号。 29

29 第5章 模拟调制系统 ◼ 5.1.5 线性调制的一般模型 ◆ 滤波法模型 在前几节的讨论基础上，可以归纳出滤波法线性调制 的一般模型如下： 按照此模型得到的输出信号时域表示式为： 按照此模型得到的输出信号频域表示式为： 式中， 只要适当选择H()，便可以得到各种幅度调制信号。  m t( ) s t m ( ) cos c  t h t ( ) s (t) [m(t) cos t] h(t) m = c  [ ( ) )] ( ) 2 1 Sm () = M  +c + M −c H  H()  h(t)

第5章模拟调制系统 ◆移相法模型 s(t)=[m(t)coso t]*h(t) 将上式展开，则可得到另一种形式的时域表示式，即 s,(t)=s,(t)cosot+s(t)sin@t 式中 S(t)=h,(t)*m(t) h,(t)=h(t)cos@t so(t)=ho(t)*m(t) ho(t)=h(t)sin@t 上式表明，sm(t)可等效为两个互为正交调制分量的合成。 由此可以得到移相法线性调制的一般模型如下： 30

30 第5章 模拟调制系统 ◆ 移相法模型 将上式展开，则可得到另一种形式的时域表示式，即 式中 上式表明，sm(t)可等效为两个互为正交调制分量的合成。 由此可以得到移相法线性调制的一般模型如下： s (t) [m(t) cos t] h(t) m = c  ( ) ( )cos ( ) in m I c Q c s t s t t s t s t = +   ( ) ( ) ( ) I I s t h t m t =  ( ) ( )cos I c h t h t t =  ( ) ( ) ( ) Q Q s t h t m t =  ( ) ( )sin Q c h t h t t = 