
信息检索与数据挖掘 2019/4/29 13 概率图模型的表示 结构:GV,E) 参数:CPTs Representation A Bayesian network(BN)represents the joint distribution of a set of n(discrete) variables,Xi,X2,...,Xn,as a directed acyclic graph (DAG)and a set of conditional probability tables(CPTs).Each node,that corresponds to a variable,has an associated CPT that contains the probability of each state of the variable given its parents in the graph.The structure of the network implies a set of conditional independence assertions,which give power to this representation. A PGM is specified by two aspects:(i)a graph,G,E),that defines the structure of the model;and(ii)a set of local functions,f(Yi),that define the parameters,where Yi is a subset of X.The joint probability is obtained by the product of the local functions: M P(X1,X2....,XN)=K f(Yi) i=1 where K is a normalization constant.This representation in terms of a graph and a set of local functions(called potentials)is the basis for inference and learning in PGMs. Advances in Computer Vision and Pattern Recognition Luis Enrique Sucar,Probabilistic Graphical Models (Principles and Applications).2015
信息检索与数据挖掘 2019/4/29 13 概率图模型的表示 Representation A Bayesian network (BN) represents the joint distribution of a set of n (discrete) variables, X1, X2, . . . , Xn, as a directed acyclic graph (DAG) and a set of conditional probability tables (CPTs). Each node, that corresponds to a variable, has an associated CPT that contains the probability of each state of the variable given its parents in the graph. The structure of the network implies a set of conditional independence assertions, which give power to this representation. Advances in Computer Vision and Pattern Recognition Luis Enrique Sucar, Probabilistic Graphical Models (Principles and Applications), 2015 结构:G(V,E) 参数:CPTs A PGM is specified by two aspects: (i) a graph, G(V, E), that defines the structure of the model; and (ii) a set of local functions, f (Yi ), that define the parameters, where Yi is a subset of X. The joint probability is obtained by the product of the local functions: where K is a normalization constant. This representation in terms of a graph and a set of local functions (called potentials) is the basis for inference and learning in PGMs

信息检索与数据挖掘 2019/4/29 14 概率图模型的推理 Inference 含有5个变量的贝叶斯网络及其表示的联合分布 D P(A.B,C.D.E)-P(AP(BAP(CBP(D B)P(EC.D) 如果观测到变量E=e,←给定证据Evidence) 想要计算变量C=c的条件概率P(cle),←推理inference) 则 Pce)=∑P(a.,bcd,e 精确推理 近似推理 Z=∑ad P(a,b,c,d,e
信息检索与数据挖掘 2019/4/29 14 概率图模型的推理 Inference P(A,B,C,D,E)=P(A)P(B|A)P(C|B)P(D|B)P(E|C,D) 含有5个变量的贝叶斯网络及其表示的联合分布 如果观测到变量E=e,给定证据(Evidence) 想要计算变量C=c的条件概率P(c|e), 推理(inference) 则 精确推理 近似推理

信息检索与数据挖掘 2019/4/29 15 概率图模型的学习 Learning ·概率图结构已知,即为参数的学习(估计) ·常用的学习方法有两类:最大似然估计 (MLE)、贝叶斯估计。前 者视模型参数为定值,后者视其为随机变量。 ·MLE在数据完备的情况下,可将参数学习问题转化为充分统计量的 计算问题,在数据不完备的情况下,采用EM算法,用迭代方式逐步 最大化p(x|)。 。 贝叶斯估计在数据完备的情况下,根据误差准则不同,可以诱导出 最大后验估计或者后验均值的估计方法,在数据不完备的情况下: 可以将0视为一种特殊的隐变量,从而问题归结为推理问题,可以 采用变分贝叶斯方法近似求解。 ·概率图结构未知 。 数据完备时,较好的方式是定义一个得分函数,评估结构与数据的 匹配程度,然后搜索最大得分的结构。实际中需要根据奥克姆剃刀 原理,选择可以拟合数据的最简单模型。如果预先假定结构是树模 型(每个节点至多有一个父节点),则搜索可在多项式时间内完成, 否则是NP-hard问题。 数据不完备,需考虑structural EM.算法。 Cmap arg max P(cld)=arg max P(c)P(tklc) cEC cEC 1<k≤nd
信息检索与数据挖掘 2019/4/29 15 概率图模型的学习 Learning • 概率图结构已知,即为参数的学习(估计) • 常用的学习方法有两类:最大似然估计(MLE)、贝叶斯估计。前 者视模型参数为定值,后者视其为随机变量。 • MLE在数据完备的情况下,可将参数学习问题转化为充分统计量的 计算问题,在数据不完备的情况下,采用EM算法,用迭代方式逐步 最大化p(x | θ)。 • 贝叶斯估计在数据完备的情况下,根据误差准则不同,可以诱导出 最大后验估计或者后验均值的估计方法,在数据不完备的情况下, 可以将 θ 视为一种特殊的隐变量,从而问题归结为推理问题,可以 采用变分贝叶斯方法近似求解。 • 概率图结构未知 • 数据完备时,较好的方式是定义一个得分函数,评估结构与数据的 匹配程度,然后搜索最大得分的结构。实际中需要根据奥克姆剃刀 原理,选择可以拟合数据的最简单模型。如果预先假定结构是树模 型(每个节点至多有一个父节点),则搜索可在多项式时间内完成, 否则是NP-hard问题。 • 数据不完备,需考虑structural EM算法

信息检索与数据挖掘 2019/4/29 16 小结:表示、推理、学习 Representation,Inference,Learning Representation ·a graph←结构:G(V,E) ·a set of local functions(called potentials)←参数:CPTs 。Inference answering different probabilistic queries based on the model and some evidence. obtain the marginal or conditional probabilities of any subset of variables Z given any other subset Y. 。Learning given a set of data values for X(that can be incomplete) estimate the structure(graph)and parameters (local functions) of the model
信息检索与数据挖掘 2019/4/29 16 小结:表示、推理、学习 Representation, Inference, Learning • Representation • a graph 结构:G(V,E) • a set of local functions (called potentials) 参数:CPTs • Inference • answering different probabilistic queries based on the model and some evidence. • obtain the marginal or conditional probabilities of any subset of variables Z given any other subset Y. • Learning • given a set of data values for X (that can be incomplete) estimate the structure (graph) and parameters (local functions) of the model
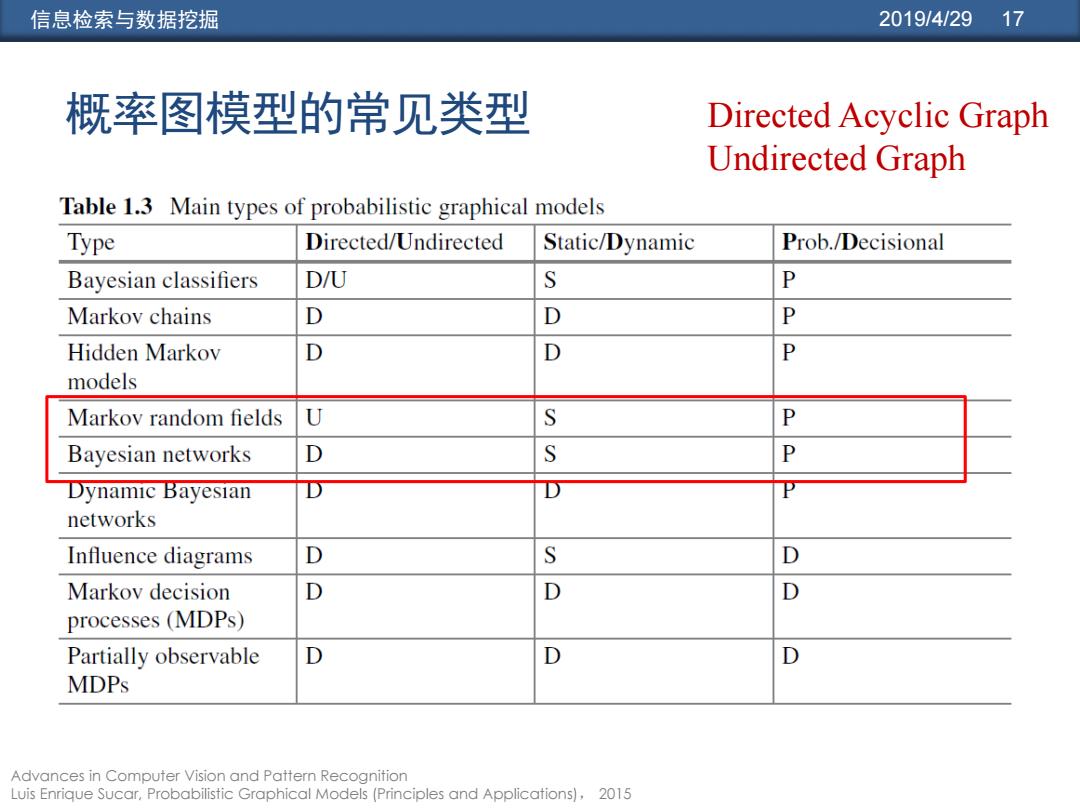
信息检索与数据挖掘 2019/4/29 17 概率图模型的常见类型 Directed Acyclic Graph Undirected Graph Table 1.3 Main types of probabilistic graphical models Type Directed/Undirected Static/Dynamic Prob./Decisional Bayesian classifiers D/U S P Markov chains D D P Hidden Markov D D P models Markov random fields U S P Bayesian networks D S P Dynamic Bayesian D networks Influence diagrams S D Markov decision D D D processes(MDPs) Partially observable D D D MDPs Advances in Computer Vision and Pattern Recognition Luis Enrique Sucar,Probabilistic Graphical Models(Principles and Applications),2015
信息检索与数据挖掘 2019/4/29 17 概率图模型的常见类型 Advances in Computer Vision and Pattern Recognition Luis Enrique Sucar, Probabilistic Graphical Models (Principles and Applications), 2015 Directed Acyclic Graph Undirected Graph