北京化二大学 第二节压延成型原理 三、流场分析 3、方程简化 ■润滑近似 当 h <1时, 0x Vy<<Vx 2h Vy≈0,Vx≠0, aVx≈ 0 Ox ay ∂x
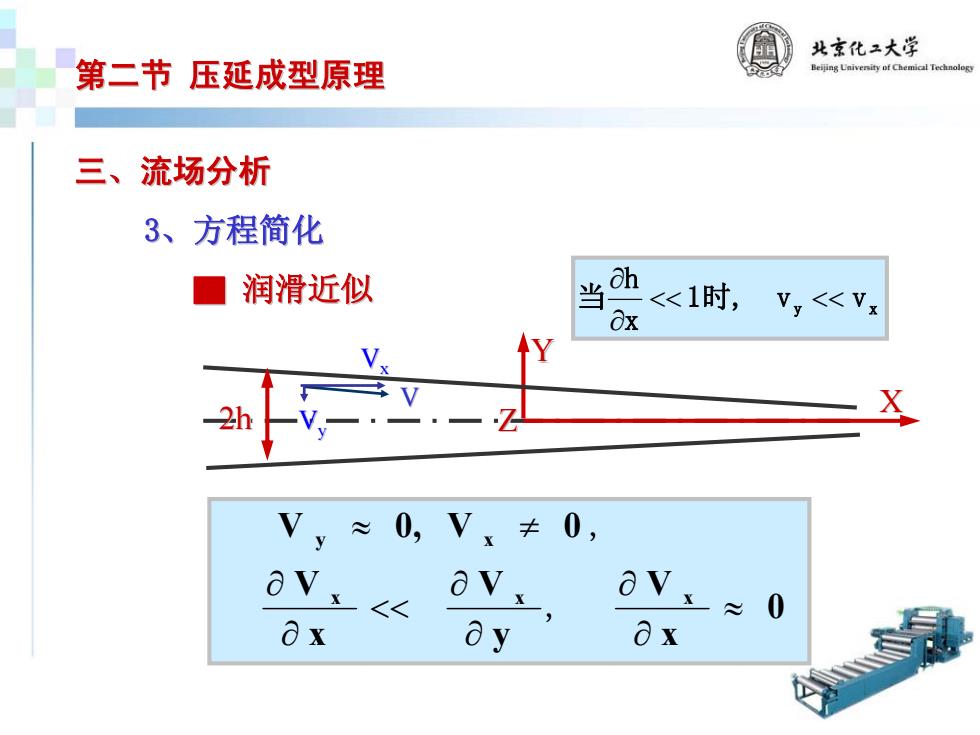
三、流场分析 第二节 压延成型原理 3、方程简化 ▇ 润滑近似 Y X 2h Z Vx Vy V xy 1时, vv xh 当 << << ∂∂ 0 x V y V x V 0V0,V x x x y x ≈ ∂ ∂ ∂ ∂ << ∂ ∂ ≈ ≠ ,

北京化二大学 第二节压延成型原理 三、流场分析 3、方程简化 aP (1) Ox dy OP =0 (2) dy Vs tx=门 (3) ay
三、流场分析 3、方程简化 第二节 压延成型原理 yx 0 x y ∂Ρ ∂τ −+ = ∂ ∂ (1) P 0 y ∂ = ∂ (2) x yx V y τ η ∂ = ∂ (3)

北京化二大学 第二节压延成型原理 四、嵌住区的速度分布和压力分布 1、速度分布方程 OP a'v Ox +1 =0 ay2 (4) o'Vs 1 aP ay2 (4) n ax aVx=」 1 dp 积分一次 y+C OP ay n dx Bx dx
四、嵌住区的速度分布和压力分布 四、嵌住区的速度分布和压力分布 第二节 压延成型原理 1、速度分布方程 、速度分布方程 2 x 2 V 0 x y Ρ η ∂ ∂ −+ = ∂ ∂ (4) 2 x 2 V 1 y x Ρ η ∂ ∂ = ⋅ ∂ ∂ (4)' dx dP x → ∂ ∂ Ρ 1 1 Cy dxdP y Vx = + ∂ ∂ η 积分一次

北京化2大学 第二节压延成型原理 四、嵌住区的速度分布和压力分布 1、速度分布方程 再积分一次】 .= ()y2+Cy+C2 2n dx y ±h 求积分常数 V V:辊筒简线速度
四、嵌住区的速度分布和压力分布 四、嵌住区的速度分布和压力分布 第二节 压延成型原理 1、速度分布方程 、速度分布方程 21 2 )( 2 1 CyCy dxdP Vx = ++ η 再积分一次 求积分常数 V:辊筒线速度 VV y h x = = ±

北京化二大学 第二节压延成型原理 四、嵌住区的速度分布和压力分布 1、速度分布方程 C1=0 dP h' 1 h=h(x) C2=v- 2n dx -) 1( Vx=V+ (5)
四、嵌住区的速度分布和压力分布 四、嵌住区的速度分布和压力分布 第二节 压延成型原理 1、速度分布方程 、速度分布方程 ( ) 2 2 x 1 dP VV yh 2 dx η =+ ⋅ − (5) = xhh )( 2 2 1 2 1 0 h dx dP vC C η −= =