
在网络思想中,把“黑箱”作为整体,对内部的 作用不研究,仅仅关心其对外的作用,并且通常把这 些对外的作用抽象到特定的区域或位置,称对外作用 的区域为端口 网络通过“端口”对外作用 黑箱
在网络思想中,把“黑箱”作为整体,对内部的 作用不研究,仅仅关心其对外的作用,并且通常把这 些对外的作用抽象到特定的区域或位置,称对外作用 的区域为端口 —— 网络通过“端口”对外作用 黑箱

通常人们总是关心在特定端口施加什么样的“输 入”,在特定的端口可以得到什么样的“输出”, 一网络注重“功能” 网络特性确定了各个端口物理量之间的关系 首先要确定端口上要研究的物理参量,比如:电 压、电流等;然后,要确定各个参量之间的关系;对 于每个端口有多个变量的情况,各个变量相互作用, 可能比较复杂
通常人们总是关心在特定端口施加什么样的“输 入” ,在特定的端口可以得到什么样的“输出” , —— 网络注重“功能” —— 网络特性确定了各个端口物理量之间的关系 首先要确定端口上要研究的物理参量,比如:电 压、电流等;然后,要确定各个参量之间的关系;对 于每个端口有多个变量的情况,各个变量相互作用, 可能比较复杂

2端口网络 a1, 比如:2端口网络,每个端口考察a和b两个物理 量,网络参数就是各个物理量之间的函数关系 lab]-f(az,bD larb2J=h(az,b) [4,a2]=g6,b2D
比如:2端口网络,每个端口考察a和b两个物理 量,网络参数就是各个物理量之间的函数关系 1 2 a1 ,b1 a2 ,b2 2 端口网络 [ ] ([ ]) 1 1 2 2 a ,b = f a ,b [ ] ([ ]) 1 2 1 2 a , a = g b ,b [ ] ([ ]) 1 2 2 1 a ,b = h a ,b
当各个参量之间是线性关系时,称网络为线性 网络,此时网络参数可以用矩阵方程表示。比如: [4,b]=f[a2,b,D d=Prdpb by=P22+p2zb2 卫12 p22
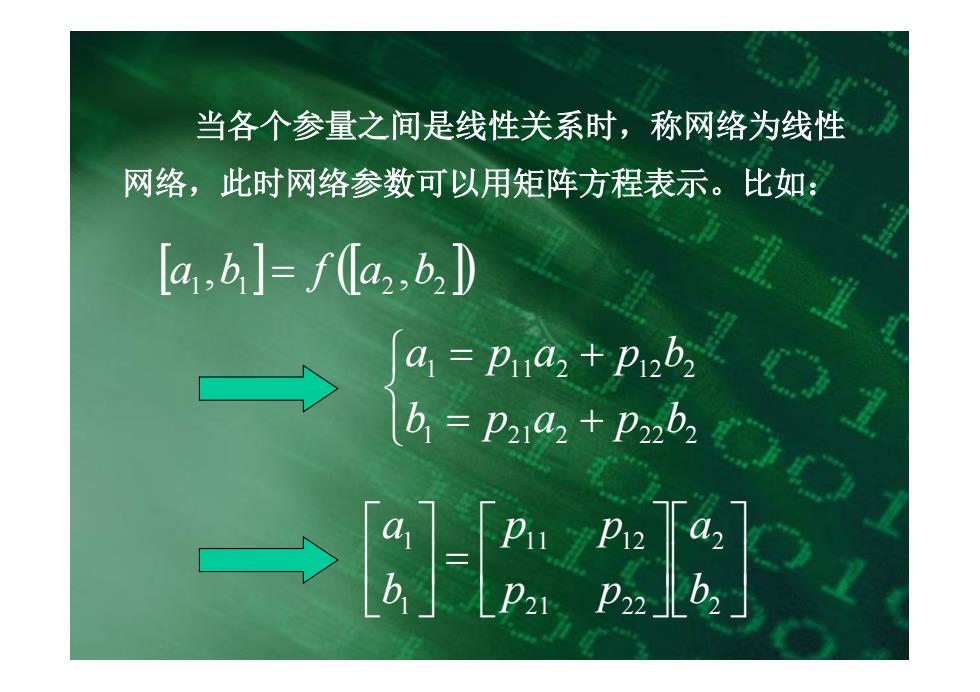
当各个参量之间是线性关系时,称网络为线性 网络,此时网络参数可以用矩阵方程表示。比如: [ ] ([ ]) 1 1 2 2 a ,b = f a ,b î í ì = + = + 1 21 2 22 2 1 11 2 12 2 b p a p b a p a p b ú û ù ê ë é ú û ù ê ë é =ú û ù ê ë é 2 2 21 22 11 12 1 1 b a p p p p b a

确定网络各个参量之间的关系,即求解网络方 程,通常有三种方法: 一是深入网络的内部,进行分析求解,得到网络参 数,称为本证的方法; 二是通过实验的方法,由多组对应参量,计算得到 网络参数; 三是大的网络由小网络连接而成,已知各个小网络 的参数及其相互连接状态,求解得到大网络参数; 网络参数有网络本身决定,通过端口数据可以 计算得到
确定网络各个参量之间的关系,即求解网络方 程,通常有三种方法: 一 是深入网络的内部,进行分析求解,得到网络参 数,称为本证的方法; 二 是通过实验的方法,由多组对应参量,计算得到 网络参数; 三 是大的网络由小网络连接而成,已知各个小网络 的参数及其相互连接状态,求解得到大网络参数; 网络参数有网络本身决定,通过端口数据可以 计算得到