
信息检索与数据挖掘 2019年4月9日 13 线性代数基础 向量可表征为特征向量的线性组合 考虑矩阵S=(?),将上述矩阵代入特征方程S入IF0可 以得到二次方程(2-)2-1=0,对这个方程求解可以得到2个特 征值=3、221,它们对应的特征向量x=(()和x(1)是正 交的。现考虑任意一个向量,如方=(), 总是可以将表示成 s的1个特征向量的线性组合,如本例:方=(径)=2.5x- 0.5x2
信息检索与数据挖掘 2019年4月9日 13 线性代数基础 向量可表征为特征向量的线性组合 考虑矩阵S = 2 1 1 2 ,将上述矩阵代入特征方程|S −λ I |= 0可 以得到二次方程 (2−λ)2−1=0,对这个方程求解可以得到2个特 征值λ1=3、λ2=1 ,它们对应的特征向量𝑥1 = 1 1 和𝑥2 1 −1 是正 交的。现考虑任意一个向量,如𝑣റ = 2 3 ,总是可以将𝑣റ表示成 S 的1个特征向量的线性组合,如本例:𝑣റ = 2 3 = 2.5𝑥1 − 0.5𝑥2

信息检索与数据挖掘 2019年4月9日 15 小结:线性代数基础 ·矩阵CMxw,其中的每个元素都是非负实数 ·rank(C)min{M,W ·方阵CMXM ·左特征向量:满足TC=λT式的M维向量)。 ·右特征向量:满足Cx=入x的M维非零向量x
信息检索与数据挖掘 2019年4月9日 15 小结:线性代数基础 • 矩阵CM×N,其中的每个元素都是非负实数 • rank(C)≤ min{M,N} • 方阵CM×M • 左特征向量:满足𝑦റ 𝑇C = λ𝑦റ 𝑇 式的M维向量𝑦റ。 • 右特征向量:满足C𝑥റ = λ𝑥റ的M维非零向量𝑥റ

信息检索与数据挖掘 2019年4月9日 16 矩阵分解在信息检索中的应用 •矩阵分解及隐性语义索引 ·关于词项-文档矩阵 ·线性代数基础 ·矩阵分解与低秩逼近 ·R中的隐性语义索引 ·矩阵分解的计算机实现 •推荐系统 ·推荐系统的兴起 ·推荐系统的基本方法 。示例:UV分解用于音乐推荐
信息检索与数据挖掘 2019年4月9日 16 矩阵分解在信息检索中的应用 • 矩阵分解及隐性语义索引 • 关于词项-文档矩阵 • 线性代数基础 • 矩阵分解与低秩逼近 • IR中的隐性语义索引 • 矩阵分解的计算机实现 • 推荐系统 • 推荐系统的兴起 • 推荐系统的基本方法 • 示例:UV分解用于音乐推荐

信息检索与数据挖掘 2019年4月9日 17 矩阵分解 方阵的分解 ·矩阵分解(matrixⅸdecomposition) ·将矩阵分解成多个矩阵因子乘积。 ·实方阵的基本因子分解方法 定理18-1(矩阵对角化定理)令S为MXM的实方阵,并且它 。 有M个线性无关的特征向量,那么存在一个特征分解:S =UU1。 ·其中,U的每一列都是S的特征向量,∧是按照特征值从大到 小排列的对角阵。 ·实对称方阵的分解方法 定理18-2(对称对角化定理)假定S是一个M×M的实对称方 。 阵,并且它有M个线性无关的特征向量,那么存在如下一个对 称对角化分解:S=Q△Q'。 。其中,O的每一列都是S的互相正交且归一化(单位长度)的 特征向量,∧是对角矩阵,其每个对角线上的值都对应S的一 个特征值。另外,由于Q是实矩阵,所以有:Q=Q严
信息检索与数据挖掘 2019年4月9日 17 矩阵分解 方阵的分解 • 矩阵分解(matrix decomposition) • 将矩阵分解成多个矩阵因子乘积。 • 实方阵的基本因子分解方法 • 定理 18-1(矩阵对角化定理) 令S 为M×M的实方阵,并且它 有M个线性无关的特征向量,那么存在一个特征分解:S =UΛU-1 。 • 其中,U 的每一列都是S 的特征向量,Λ 是按照特征值从大到 小排列的对角阵。 • 实对称方阵的分解方法 • 定理18-2(对称对角化定理) 假定S 是一个M×M的实对称方 阵,并且它有M个线性无关的特征向量,那么存在如下一个对 称对角化分解:S = QΛQT 。 • 其中,Q 的每一列都是S 的互相正交且归一化(单位长度)的 特征向量,Λ 是对角矩阵,其每个对角线上的值都对应S 的一 个特征值。另外,由于Q是实矩阵,所以有:Q-1= QT
信息检索与数据挖掘 2019年4月9日 18 矩阵分解 MXN矩阵C分解,MN ·给定MXN矩阵C,U是一个MXM的矩阵,其每 一列是矩阵CCT的正交特征向量,而NXN矩阵V 的每一列都是矩阵CC的正交特征向量。这里CT是 C的转置矩阵。 ·定理18-3令r是M×N矩阵C的秩,那么C存在如 下形式的奇异值分解(SVD):C=UUΣVI。其中 ·1.CCT的特征值1,2,.,等于CC的特征值; ·2.对于1≤i≤,令o=√见1,并且1:≥1+1。MXN的矩 阵Σ满足∑ii=o,其中1≤还r,而Σ中其他元素均为0。 o:就是矩阵C的奇异 值(singular value) VT
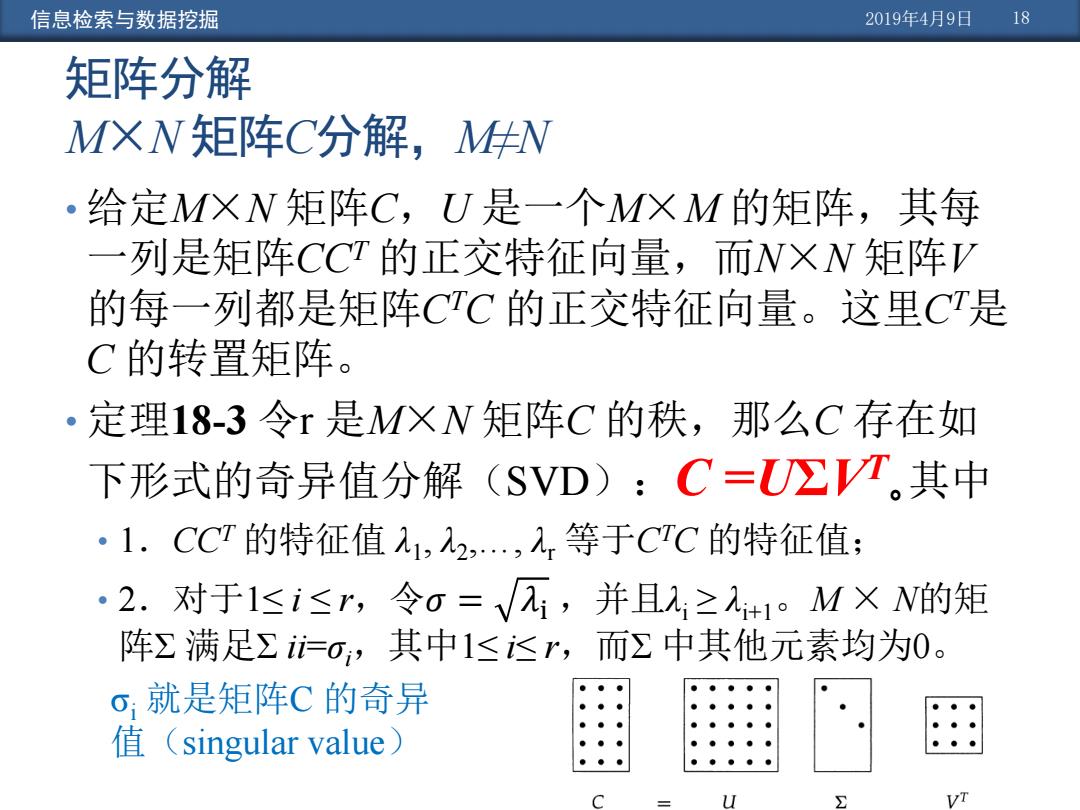
信息检索与数据挖掘 2019年4月9日 18 矩阵分解 M×N 矩阵C分解,M≠N • 给定M×N 矩阵C,U 是一个M×M 的矩阵,其每 一列是矩阵CCT 的正交特征向量,而N×N 矩阵V 的每一列都是矩阵CTC 的正交特征向量。这里CT是 C 的转置矩阵。 • 定理18-3 令r 是M×N 矩阵C 的秩,那么C 存在如 下形式的奇异值分解(SVD):C =UΣVT 。其中 • 1.CCT 的特征值 λ1 , λ2 ,…, λr 等于CTC 的特征值; • 2.对于1≤ i ≤ r,令𝜎 = 𝜆i ,并且λi ≥ λi+1。M × N的矩 阵Σ 满足Σ ii=σi,其中1≤ i≤ r,而Σ 中其他元素均为0。 σi 就是矩阵C 的奇异 值(singular value)