
书籍下载qg群6089740钉钉群21734177 IT书籍http:/L.cn/RDIAj5D 没有必要通读每个算法的详细描述,但理解模型可以让你更好地理解机器学习算法的各种 工作原理。本章还可以用作参考指南,当你不确定某个算法的工作原理时,就可以回来查 看本章内容。 2.3.1一些样本数据集 我们将使用一些数据集来说明不同的算法。其中一些数据集很小,而且是模拟的,其目的 是强调算法的某个特定方面。其他数据集都是现实世界的大型数据集。 一个模拟的二分类数据集示例是fo「ge数据集,它有两个特征。下列代码将绘制一个散点 图(图2-2),将此数据集的所有数据点可视化。图像以第一个特征为x轴,第二个特征为 y轴。正如其他散点图那样,每个数据点对应图像中的一点。每个点的颜色和形状对应其 类别: In[2]: #生成数据集 X,y mglearn.datasets.make_forge() #数据集绘图 mglearn.discrete_scatter(X[:0],x[:,1],y) plt.legend(["Class 0","Class 1"],loc=4) plt.xlabel("First feature") plt.ylabel("Second feature") print("X.shape:{}"format(X.shape)) 0ut[2]: X.shape:(26,2) 0 】 Class 0 Class 1 9 10 11 12 First feature 图2-2:forge数据集的散点图 监督学习125 电子书寻找看手相钉钉或微信pythontesting
监督学习 | 25 没有必要通读每个算法的详细描述,但理解模型可以让你更好地理解机器学习算法的各种 工作原理。本章还可以用作参考指南,当你不确定某个算法的工作原理时,就可以回来查 看本章内容。 2.3.1 一些样本数据集 我们将使用一些数据集来说明不同的算法。其中一些数据集很小,而且是模拟的,其目的 是强调算法的某个特定方面。其他数据集都是现实世界的大型数据集。 一个模拟的二分类数据集示例是 forge 数据集,它有两个特征。下列代码将绘制一个散点 图(图 2-2),将此数据集的所有数据点可视化。图像以第一个特征为 x 轴,第二个特征为 y 轴。正如其他散点图那样,每个数据点对应图像中的一点。每个点的颜色和形状对应其 类别: In[2]: # 生成数据集 X, y = mglearn.datasets.make_forge() # 数据集绘图 mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.legend(["Class 0", "Class 1"], loc=4) plt.xlabel("First feature") plt.ylabel("Second feature") print("X.shape: {}".format(X.shape)) Out[2]: X.shape: (26, 2) 图 2-2:forge 数据集的散点图 书籍下载qq群6089740 钉钉群21734177 IT书籍 http://t.cn/RDIAj5D 电子书寻找看手相 钉钉或微信pythontesting
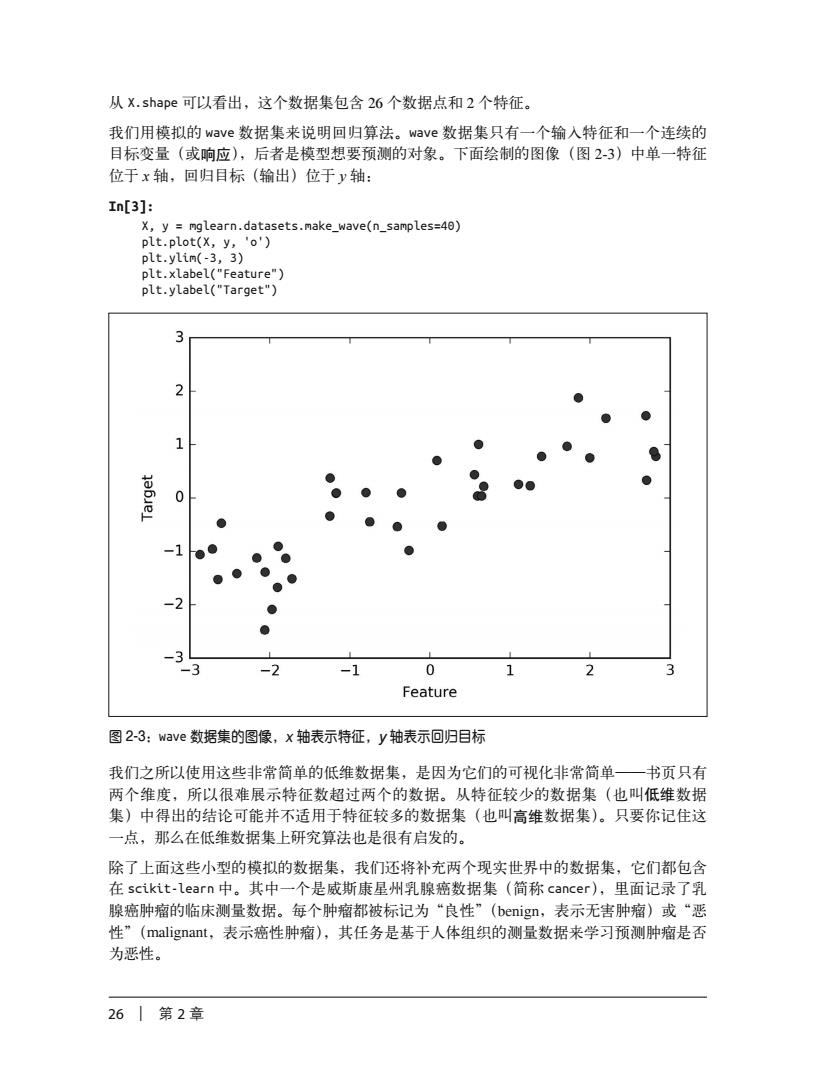
从X.shape可以看出,这个数据集包含26个数据点和2个特征。 我们用模拟的wave数据集来说明回归算法。wave数据集只有一个输入特征和一个连续的 目标变量(或响应),后者是模型想要预测的对象。下面绘制的图像(图2-3)中单一特征 位于x轴,回归目标(输出)位于y轴: In[3]: X,y mglearn.datasets.make_wave(n_samples=40) plt.plot(X,y,'o') plt.ylim(-3,3) plt.xlabel("Feature") plt.ylabel("Target") -1 3 -2 0 Feature 图2-3:wave数据集的图像,x轴表示特征,y轴表示回归目标 我们之所以使用这些非常简单的低维数据集,是因为它们的可视化非常简单一书页只有 两个维度,所以很难展示特征数超过两个的数据。从特征较少的数据集(也叫低维数据 集)中得出的结论可能并不适用于特征较多的数据集(也叫高维数据集)。只要你记住这 一点,那么在低维数据集上研究算法也是很有启发的。 除了上面这些小型的模拟的数据集,我们还将补充两个现实世界中的数据集,它们都包含 在scikit-learn中。其中一个是威斯康星州乳腺癌数据集(简称cancer),里面记录了乳 腺癌肿瘤的临床测量数据。每个肿瘤都被标记为“良性”(benign,表示无害肿瘤)或“恶 性”(malignant,表示癌性肿瘤),其任务是基于人体组织的测量数据来学习预测肿瘤是否 为恶性。 26 |第2章
26 | 第 2 章 从 X.shape 可以看出,这个数据集包含 26 个数据点和 2 个特征。 我们用模拟的 wave 数据集来说明回归算法。wave 数据集只有一个输入特征和一个连续的 目标变量(或响应),后者是模型想要预测的对象。下面绘制的图像(图 2-3)中单一特征 位于 x 轴,回归目标(输出)位于 y 轴: In[3]: X, y = mglearn.datasets.make_wave(n_samples=40) plt.plot(X, y, 'o') plt.ylim(-3, 3) plt.xlabel("Feature") plt.ylabel("Target") 图 2-3:wave 数据集的图像,x 轴表示特征,y 轴表示回归目标 我们之所以使用这些非常简单的低维数据集,是因为它们的可视化非常简单——书页只有 两个维度,所以很难展示特征数超过两个的数据。从特征较少的数据集(也叫低维数据 集)中得出的结论可能并不适用于特征较多的数据集(也叫高维数据集)。只要你记住这 一点,那么在低维数据集上研究算法也是很有启发的。 除了上面这些小型的模拟的数据集,我们还将补充两个现实世界中的数据集,它们都包含 在 scikit-learn 中。其中一个是威斯康星州乳腺癌数据集(简称 cancer),里面记录了乳 腺癌肿瘤的临床测量数据。每个肿瘤都被标记为“良性”(benign,表示无害肿瘤)或“恶 性”(malignant,表示癌性肿瘤),其任务是基于人体组织的测量数据来学习预测肿瘤是否 为恶性

书籍下载qq群6089740钉钉群21734177 IT书籍http://t.cn/RDIAj5D 可以用scikit-learn模块的load_breast_cancer函数来加载数据: In[4]: from sklearn.datasets import load breast cancer cancer load_breast_cancer() print("cancer.keys():\n{]".format(cancer.keys())) 0ut[4]: cancer.keys(): dict_keys(['feature_names','data','DESCR','target','target_names']) 包含在scikit-learn中的数据集通常被保存为Bunch对象,里面包含真实 数据以及一些数据集信息。关于Buch对象,你只需要知道它与字典很相 似,而且还有一个额外的好处,就是你可以用点操作符来访问对象的值(比 如用bunch.key来代替bunch['key']). 这个数据集共包含569个数据点,每个数据点有30个特征: In[5]: print("Shape of cancer data:{]"format(cancer.data.shape)) 0ut[5]: Shape of cancer data:(569,30) 在569个数据点中,212个被标记为恶性,357个被标记为良性: In[6]: print("Sample counts per class:\n{]".format( {n:v for n,v in zip(cancer.target_names,np.bincount(cancer.target))])) 0ut[6]: Sample counts per class: {"benign":357,"malignant":212} 为了得到每个特征的语义说明,我们可以看一下feature_.names属性: In[7]: print("Feature names:\n{}".format(cancer.feature_names)) 0ut[7]: Feature names: ['mean radius''mean texture''mean perimeter''mean area' 'mean smoothness''mean compactness''mean concavity' 'mean concave points''mean symmetry''mean fractal dimension' 'radius error''texture error''perimeter error''area error' 'smoothness error''compactness error''concavity error' 'concave points error''symmetry error''fractal dimension error' 'worst radius''worst texture''worst perimeter''worst area' 'worst smoothness''worst compactness''worst concavity' 'worst concave points''worst symmetry''worst fractal dimension'] 感兴趣的话,你可以阅读cancer.DESCR来了解数据的更多信息。 监督学习27 电子书寻找看手相钉钉或微信pythontesting
监督学习 | 27 可以用 scikit-learn 模块的 load_breast_cancer 函数来加载数据: In[4]: from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() print("cancer.keys(): \n{}".format(cancer.keys())) Out[4]: cancer.keys(): dict_keys(['feature_names', 'data', 'DESCR', 'target', 'target_names']) 包含在 scikit-learn 中的数据集通常被保存为 Bunch 对象,里面包含真实 数据以及一些数据集信息。关于 Bunch 对象,你只需要知道它与字典很相 似,而且还有一个额外的好处,就是你可以用点操作符来访问对象的值(比 如用 bunch.key 来代替 bunch['key'])。 这个数据集共包含 569 个数据点,每个数据点有 30 个特征: In[5]: print("Shape of cancer data: {}".format(cancer.data.shape)) Out[5]: Shape of cancer data: (569, 30) 在 569 个数据点中,212 个被标记为恶性,357 个被标记为良性: In[6]: print("Sample counts per class:\n{}".format( {n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))})) Out[6]: Sample counts per class: {'benign': 357, 'malignant': 212} 为了得到每个特征的语义说明,我们可以看一下 feature_names 属性: In[7]: print("Feature names:\n{}".format(cancer.feature_names)) Out[7]: Feature names: ['mean radius' 'mean texture' 'mean perimeter' 'mean area' 'mean smoothness' 'mean compactness' 'mean concavity' 'mean concave points' 'mean symmetry' 'mean fractal dimension' 'radius error' 'texture error' 'perimeter error' 'area error' 'smoothness error' 'compactness error' 'concavity error' 'concave points error' 'symmetry error' 'fractal dimension error' 'worst radius' 'worst texture' 'worst perimeter' 'worst area' 'worst smoothness' 'worst compactness' 'worst concavity' 'worst concave points' 'worst symmetry' 'worst fractal dimension'] 感兴趣的话,你可以阅读 cancer.DESCR 来了解数据的更多信息。 书籍下载qq群6089740 钉钉群21734177 IT书籍 http://t.cn/RDIAj5D 电子书寻找看手相 钉钉或微信pythontesting

我们还会用到一个现实世界中的回归数据集,即波士顿房价数据集。与这个数据集相关的 任务是,利用犯罪率、是否邻近查尔斯河、公路可达性等信息,来预测20世纪70年代波 士顿地区房屋价格的中位数。这个数据集包含506个数据点和13个特征: In[8]: from sklearn.datasets import load boston boston load boston() print("Data shape:{]"format(boston.data.shape)) 0ut[8]: Data shape:(506,13) 同样,你可以阅读boston对象的DESCR属性来了解数据集的更多信息。对于我们的目的 而言,我们需要扩展这个数据集,输入特征不仅包括这13个测量结果,还包括这些特征 之间的乘积(也叫交互项)。换句话说,我们不仅将犯罪率和公路可达性作为特征,还将 犯罪率和公路可达性的乘积作为特征。像这样包含导出特征的方法叫作特征工程(feature engineering),将在第4章中详细讲述。这个导出的数据集可以用load_extended_.boston函 数加载: In[9]: X,y mglearn.datasets.Load_extended_boston() print("X.shape:{]"format(X.shape)) 0ut[9]: X.shape:(506,104) 最初的13个特征加上这13个特征两两组合(有放回)得到的91个特征,一共有104个 特征。5 我们将利用这些数据集对不同机器学习算法的性质进行解释说明。但目前来说,先来看算 法本身。首先重新学习上一章见过的k近邻(k-NN)算法。 2.3.2k近邻 k-NN算法可以说是最简单的机器学习算法。构建模型只需要保存训练数据集即可。想要 对新数据点做出预测,算法会在训练数据集中找到最近的数据点,也就是它的“最近邻”。 1.k近邻分类 k-NN算法最简单的版本只考虑一个最近邻,也就是与我们想要预测的数据点最近的训练 数据点。预测结果就是这个训练数据点的已知输出。图2-4给出了这种分类方法在fo「ge 数据集上的应用: In[10]: mglearn.plots.plot_knn_classification(n_neighbors=1) 注5:第1个特征可以与13个特征相乘,第2个可以与12个特征相乘(除了第1个),第3个可以与11个 特征相乘…依次相加,13+12+11+…+1=91。 281 第2章
28 | 第 2 章 我们还会用到一个现实世界中的回归数据集,即波士顿房价数据集。与这个数据集相关的 任务是,利用犯罪率、是否邻近查尔斯河、公路可达性等信息,来预测 20 世纪 70 年代波 士顿地区房屋价格的中位数。这个数据集包含 506 个数据点和 13 个特征: In[8]: from sklearn.datasets import load_boston boston = load_boston() print("Data shape: {}".format(boston.data.shape)) Out[8]: Data shape: (506, 13) 同样,你可以阅读 boston 对象的 DESCR 属性来了解数据集的更多信息。对于我们的目的 而言,我们需要扩展这个数据集,输入特征不仅包括这 13 个测量结果,还包括这些特征 之间的乘积(也叫交互项)。换句话说,我们不仅将犯罪率和公路可达性作为特征,还将 犯罪率和公路可达性的乘积作为特征。像这样包含导出特征的方法叫作特征工程(feature engineering),将在第 4 章中详细讲述。这个导出的数据集可以用 load_extended_boston 函 数加载: In[9]: X, y = mglearn.datasets.load_extended_boston() print("X.shape: {}".format(X.shape)) Out[9]: X.shape: (506, 104) 最初的 13 个特征加上这 13 个特征两两组合(有放回)得到的 91 个特征,一共有 104 个 特征。5 我们将利用这些数据集对不同机器学习算法的性质进行解释说明。但目前来说,先来看算 法本身。首先重新学习上一章见过的 k 近邻(k-NN)算法。 2.3.2 k近邻 k-NN 算法可以说是最简单的机器学习算法。构建模型只需要保存训练数据集即可。想要 对新数据点做出预测,算法会在训练数据集中找到最近的数据点,也就是它的“最近邻”。 1. k近邻分类 k-NN 算法最简单的版本只考虑一个最近邻,也就是与我们想要预测的数据点最近的训练 数据点。预测结果就是这个训练数据点的已知输出。图 2-4 给出了这种分类方法在 forge 数据集上的应用: In[10]: mglearn.plots.plot_knn_classification(n_neighbors=1) 注 5:第 1 个特征可以与 13 个特征相乘,第 2 个可以与 12 个特征相乘(除了第 1 个),第 3 个可以与 11 个 特征相乘……依次相加,13 + 12 + 11 + … + 1 = 91

书籍下载qg群6089740钉钉群21734177 IT书籍http:/t.cn/RDIAj5D ● training class 0 training class 1 ★ test pred 0 ★ test pred 1 9 10 11 12 图2-4:单一最近邻模型对forge数据集的预测结果 这里我们添加了3个新数据点(用五角星表示)。对于每个新数据点,我们标记了训练集 中与它最近的点。单一最近邻算法的预测结果就是那个点的标签(对应五角星的颜色)。 除了仅考虑最近邻,我还可以考虑任意个(k个)邻居。这也是k近邻算法名字的来历 在考虑多于一个邻居的情况时,我们用“投票法”(vog)来指定标签。也就是说,对 于每个测试点,我们数一数多少个邻居属于类别0,多少个邻居属于类别1。然后将出现 次数更多的类别(也就是k个近邻中占多数的类别)作为预测结果。下面的例子(图2-5) 用到了3个近邻: In[11]: mglearn.plots.plot_knn_classification(n_neighbors=3) ● training class o training class 1 ★ test pred 0 test pred 1 10 11 12 图2-5:3近邻模型对forge数据集的预测结果 监督学习129 电子书寻找看手相钉钉或微信pythontesting图灵社区会员zhugeln(499702878@qq,com)专享尊重版权
监督学习 | 29 图 2-4:单一最近邻模型对 forge 数据集的预测结果 这里我们添加了 3 个新数据点(用五角星表示)。对于每个新数据点,我们标记了训练集 中与它最近的点。单一最近邻算法的预测结果就是那个点的标签(对应五角星的颜色)。 除了仅考虑最近邻,我还可以考虑任意个(k 个)邻居。这也是 k 近邻算法名字的来历。 在考虑多于一个邻居的情况时,我们用“投票法”(voting)来指定标签。也就是说,对 于每个测试点,我们数一数多少个邻居属于类别 0,多少个邻居属于类别 1。然后将出现 次数更多的类别(也就是 k 个近邻中占多数的类别)作为预测结果。下面的例子(图 2-5) 用到了 3 个近邻: In[11]: mglearn.plots.plot_knn_classification(n_neighbors=3) 图 2-5:3 近邻模型对 forge 数据集的预测结果 图灵社区会员 zhugeln(499702878@qq.com) 专享 尊重版权 书籍下载qq群6089740 钉钉群21734177 IT书籍 http://t.cn/RDIAj5D 电子书寻找看手相 钉钉或微信pythontesting