
二、对流换热基本方程 质量守恒方程 2+ao四+ap四+pm-0 向量形式 +di(o)-架+p.(p)=0 div(pV):散度 div(pV)-(pw tu dt +哭+w架+p袋+器+的-0→ニ+n0.v=+pdiv-0 ax ax ax DT D 全导数 Dp,ap,p,∂p Dt +u- +w Dt Ot -+ 0x 0x 张量形式 dp a -(pv)=0 i=1,2,3 DP-0 ou 不可压缩流体p为常数 Dt divvax av,aw、 =0 ay
二、对流换热基本方程 质量守恒方程 𝜕𝜌 𝜕𝜏 + 𝜕(𝜌𝑢) 𝜕𝑥 + 𝜕(𝜌𝑣) 𝜕𝑥 + 𝜕(𝜌𝑤) 𝜕𝑥 =0 向量形式 𝜕𝜌 𝜕𝜏 + 𝑑𝑖𝑣(𝜌𝑽) = 𝜕𝜌 𝜕𝜏 + 𝛻 ∙ (𝜌𝑽) =0 𝑑𝑖𝑣 𝜌𝑽 :散度 𝑑𝑖𝑣 𝜌𝑽 = 𝜕(𝜌𝑢) 𝜕𝑥 + 𝜕(𝜌𝑣) 𝜕𝑥 + 𝜕(𝜌𝑤) 𝜕𝑥 𝜕𝜌 𝜕𝜏 + 𝑢 𝜕𝜌 𝜕𝑥 + 𝑣 𝜕𝜌 𝜕𝑥 + 𝑤 𝜕𝜌 𝜕𝑥 + 𝜌( 𝜕𝑢 𝜕𝑥 + 𝜕𝑣 𝜕𝑦 + 𝜕𝑤 𝜕𝑧 )=0 𝐷𝜌 𝐷𝜏 + 𝜌𝛻 ∙ 𝑽 = 𝐷𝜌 𝐷𝜏 + 𝜌𝑑𝑖𝑣𝑽=0 𝐷 𝐷𝜏 全导数 𝐷 𝐷𝜏 = 𝜕𝜌 𝜕𝜏 + 𝑢 𝜕𝜌 𝜕𝑥 + 𝑣 𝜕𝜌 𝜕𝑥 + 𝑤 𝜕𝜌 𝜕𝑥 张量形式 𝜕𝜌 𝜕𝜏 + 𝜕 𝜕𝑥𝑖 𝜌𝑣𝑖 = 0 𝑖 = 1,2,3 不可压缩流体 𝜌为常数 𝐷𝜌 𝐷𝜏 =0 𝑑𝑖𝑣𝑽( 𝜕𝑢 𝜕𝑥 + 𝜕𝑣 𝜕𝑦 + 𝜕𝑤 𝜕𝑧 )=0

二、对流换热基本方程 动量守恒方程 du Ju ou au ap 2u p +u + +w 0x dy 0z ax +n ax2+ dy2+ 0z2 +Fx av ap /a2v2v 02v dy +w 0z dy +n (Ox2+ 0z2 +F Ow Ow Ow Ow ap a2w.∂2w. dy +w 0z dz+n ax2+ dy2+ 0z2 +F2 向量形式 DV =-7p+n72V+F
二、对流换热基本方程 动量守恒方程 向量形式 𝜌 𝐷𝑽 𝐷𝜏 = −𝛻𝑝 + 𝜂𝛻 2𝑽 + 𝑭 𝜌 𝜕𝑢 𝜕𝜏 + 𝑢 𝜕𝑢 𝜕𝑥 + 𝑣 𝜕𝑢 𝜕𝑦 + 𝑤 𝜕𝑢 𝜕𝑧 = − 𝜕𝑝 𝜕𝑥 + 𝜂 𝜕 2𝑢 𝜕𝑥 2 + 𝜕 2𝑢 𝜕𝑦 2 + 𝜕 2𝑢 𝜕𝑧 2 + 𝐹𝑥 𝜌 𝜕𝑣 𝜕𝜏 + 𝑢 𝜕𝑣 𝜕𝑥 + 𝑣 𝜕𝑣 𝜕𝑦 + 𝑤 𝜕𝑣 𝜕𝑧 = − 𝜕𝑝 𝜕𝑦 + 𝜂 𝜕 2𝑣 𝜕𝑥 2 + 𝜕 2𝑣 𝜕𝑦 2 + 𝜕 2𝑣 𝜕𝑧 2 + 𝐹𝑦 𝜌 𝜕𝑤 𝜕𝜏 + 𝑢 𝜕𝑤 𝜕𝑥 + 𝑣 𝜕𝑤 𝜕𝑦 + 𝑤 𝜕𝑤 𝜕𝑧 = − 𝜕𝑝 𝜕𝑧 + 𝜂 𝜕 2𝑤 𝜕𝑥 2 + 𝜕 2𝑤 𝜕𝑦 2 + 𝜕 2𝑤 𝜕𝑧 2 + 𝐹𝑧

二、对流换热基本方程 能量守恒方程 p,(儒+贺+部+w)=品(a贺)+品(的)品(a韶) p,咒-品(的)+()品(韶 向量形式 DT pop Di =7·(λ7T) Ot p+v.T)=7·(☑Tm)
二、对流换热基本方程 能量守恒方程 𝜌𝑐𝑝 𝜕𝑇 𝜕𝜏 + 𝑢 𝜕𝑇 𝜕𝑥 + 𝑣 𝜕𝑇 𝜕𝑦 + 𝑤 𝜕𝑇 𝜕𝑧 = 𝜕 𝜕𝑥 𝜆 𝜕𝑇 𝜕𝑥 + 𝜕 𝜕𝑦 𝜆 𝜕𝑇 𝜕𝑦 + 𝜕 𝜕𝑧 𝜆 𝜕𝑇 𝜕𝑧 𝜌𝑐𝑝 𝐷𝑇 𝐷𝜏 = 𝜕 𝜕𝑥 𝜆 𝜕𝑇 𝜕𝑥 + 𝜕 𝜕𝑦 𝜆 𝜕𝑇 𝜕𝑦 + 𝜕 𝜕𝑧 𝜆 𝜕𝑇 𝜕𝑧 向量形式 𝜌𝑐𝑝 𝐷𝑇 𝐷𝜏 = 𝛻 ∙ (𝜆𝛻𝑇) 𝜌𝑐𝑝( 𝜕𝑇 𝜕𝜏 + 𝑽 ∙ 𝛻𝑇) = 𝛻 ∙ (𝜆𝛻𝑇)
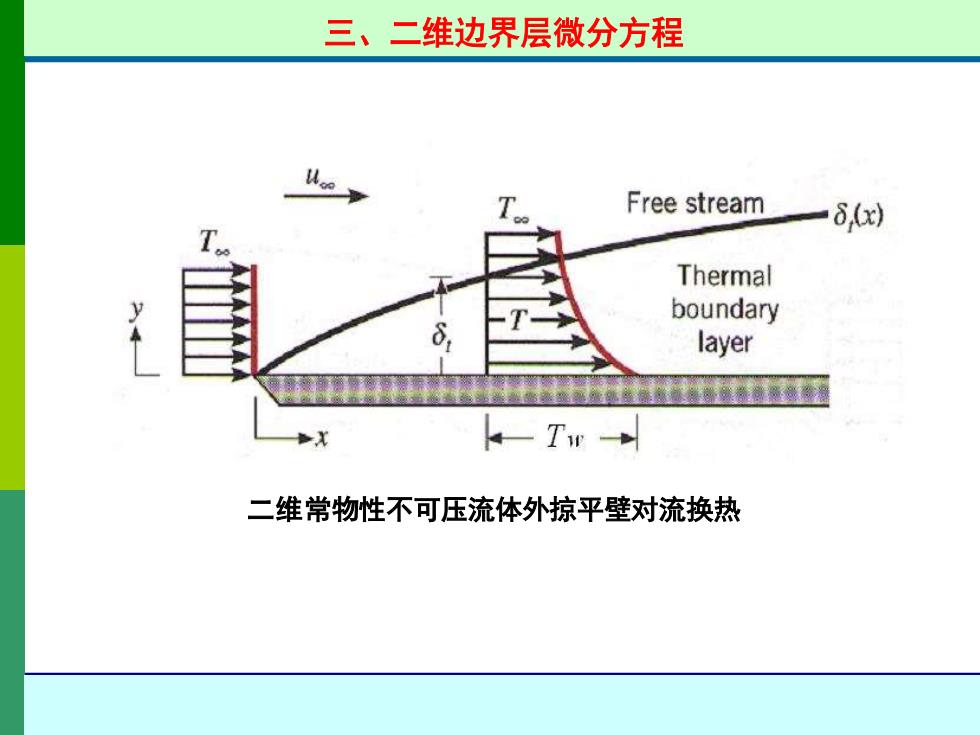
三、二维边界层微分方程 T Free stream 一8,x Thermal boundary layer 一Tw 二维常物性不可压流体外掠平壁对流换热
三、二维边界层微分方程 二维常物性不可压流体外掠平壁对流换热

三、二维边界层微分方程 二维边界层微分方程 du ov x+ =0 ou ap a2u,∂2u x +) 8x +nox2+ y2 dv av op 02v02v u dy +nx2+ dy 2) OT u ∂y =a( x2+ 0y2) λ Ot 5个方程,5个未知量 hx= tw-toody y=0.x 理论上可解
三、二维边界层微分方程 二维边界层微分方程 𝜕𝑢 𝜕𝑥 + 𝜕𝑣 𝜕𝑦 = 0 𝜌 𝑢 𝜕𝑢 𝜕𝑥 + 𝑣 𝜕𝑢 𝜕𝑦 = − 𝜕𝑝 𝜕𝑥 + 𝜂( 𝜕 2𝑢 𝜕𝑥 2 + 𝜕 2𝑢 𝜕𝑦 2 ) 𝜌 𝑢 𝜕𝑣 𝜕𝑥 + 𝑣 𝜕𝑣 𝜕𝑦 = − 𝜕𝑝 𝜕𝑦 + 𝜂( 𝜕 2𝑣 𝜕𝑥 2 + 𝜕 2𝑣 𝜕𝑦 2 ) 𝑢 𝜕𝑇 𝜕𝑥 + 𝑣 𝜕𝑇 𝜕𝑦 = 𝛼( 𝜕 2𝑇 𝜕𝑥 2 + 𝜕 2𝑇 𝜕𝑦 2 ) ℎ𝑥 = 𝜆 𝑡𝑊 − 𝑡∞ ቤ 𝜕𝑡 𝜕𝑦 𝑦=0,𝑥 5个方程,5个未知量 理论上可解