斐波那契数列的递归求解过程 调用次数NumCall(k)=2k-1-1 ■fibonacci(5)的递归求解过程: 算法复杂度:O(2n) Fb⑤ Fib④) Fib(3) Fib (3) Fib (2) Fib(2) Fh(1) Fb②) Fib(1) Fib(1) Fb(@) Fb(1) Fib(O) F(1) Fib(0)
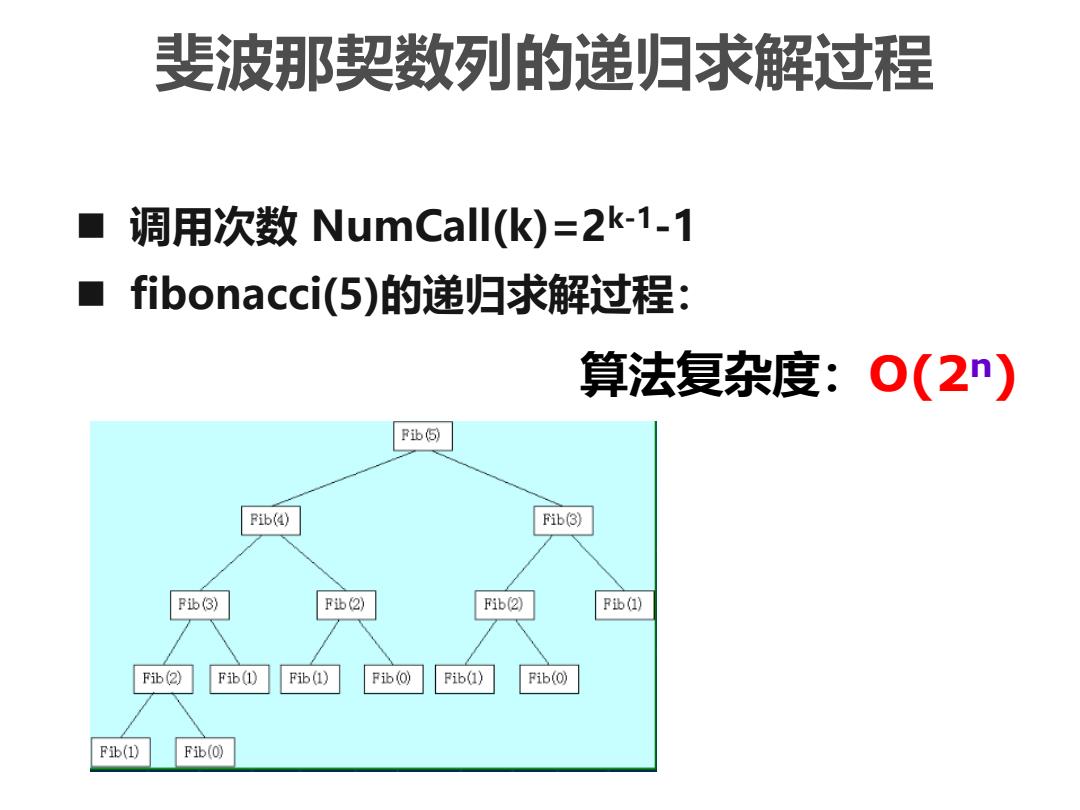
斐波那契数列的递归求解过程 ◼ 调用次数 NumCall(k)=2k-1-1 ◼ fibonacci(5)的递归求解过程: 算法复杂度:O(2n)

斐波纳契数列解法2:递推 递归解法的问题在于:重复求解子问题 观察Fib(n)的定义:F(n)=F(n-1)+F(n-2):(n>=2) F()具有“无后效性”:只需“记住”前两个状态的结果即可 long fib2(int n) long f1 1,f2 1,fu; for(int i=2;i<=n;++i) fu f1 f2; f1=f2;f2=fu;//记忆 } return fu; 算法复杂度:O(n) }
斐波纳契数列解法2:递推 long fib2(int n){ long f1 = 1, f2 = 1, fu; for(int i = 2; i <= n; ++i){ fu = f1 + f2; f1 = f2; f2 = fu; // 记忆 } return fu; } 算法复杂度:O(n) 递归解法的问题在于:重复求解子问题 观察Fib(n)的定义:F(n) = F(n-1) + F(n-2); (n>=2) F(n) 具有“无后效性”:只需“记住”前两个状态的结果即可

递归的应用场景(2) 问题采用的数据结构是递归的
递归的应用场景(2) 问题采用的数据结构是递归的
递归算法示例2:数据结构是递归的 二叉树链式存储结构:二叉链表 Ichild data rchild typedef struct i node Entrytype data; struct node *lchild,*rchild; BTNode,*BTPtr; B c E FA 有多少指针为空? G 在n个结点的二叉链表中,有n+1个空指针域
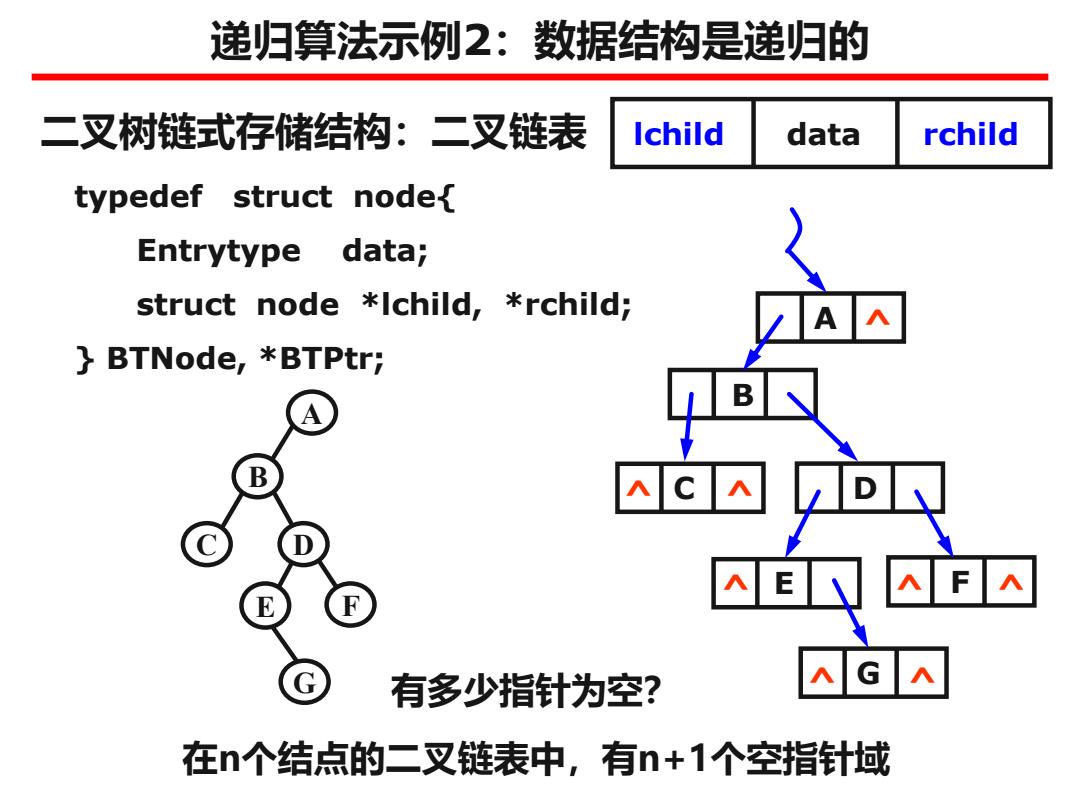
二叉树链式存储结构:二叉链表 typedef struct node{ Entrytype data; struct node *lchild, *rchild; } BTNode, *BTPtr; lchild data rchild A B C D E F G 在n个结点的二叉链表中,有n+1个空指针域 A B C D E F G ^ ^ ^ ^ ^ ^ 有多少指针为空? ^ ^ 递归算法示例2:数据结构是递归的
3中序遍历递归算法 A void inorder BTPtr bt) if(bt !NULL) B inorder bt->Ichild ) printf ("%c\t",bt->data); inorder bt->rchild ) 3后序遍历递归算法 } void postorder(BTPtr bt){ return; if(bt !NULL) } postorder(bt->lchild ) postorder(bt->rchild ) 中序序列:BDAC printf ("%c\t",bt->data) } 后序序列:DBCA return; }
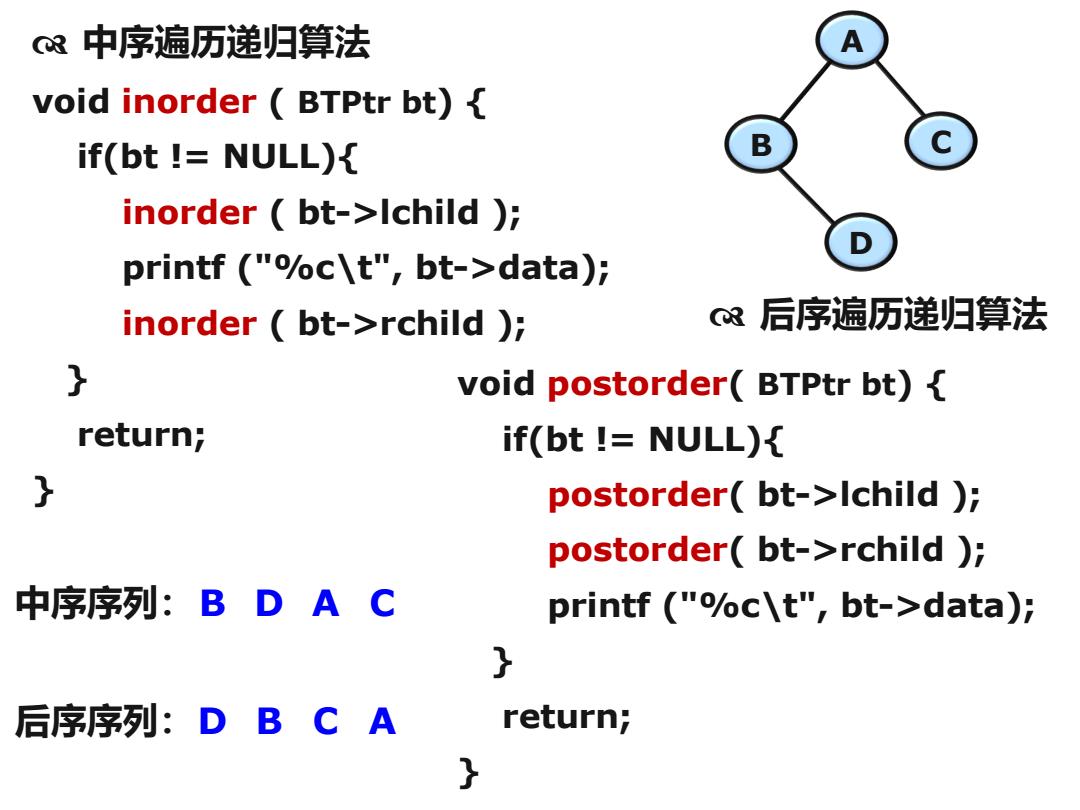
void inorder ( BTPtr bt) { if(bt != NULL){ inorder ( bt->lchild ); printf ("%c\t", bt->data); inorder ( bt->rchild ); } return; } 中序遍历递归算法 A B C D 中序序列:B D A C void postorder( BTPtr bt) { if(bt != NULL){ postorder( bt->lchild ); postorder( bt->rchild ); printf ("%c\t", bt->data); } return; } 后序遍历递归算法 后序序列:D B C A