案例1 《计算基本描述统计量》的应用举例 对某地区居民储蓄情况进行调查,所得部分数据见附表。对一次存(取)款金 额变量计算基本描述统计量。有以下两个分析目标, 目标一:计算存(取)款金额的基本描述统计量,并分别对城镇储户和农村储 户进行比较。 目标二:分析储户一次存(取)款的数量是否存在不均衡现象。 为实现上述分析目标,利用基本描述统计分别做如下分析。 1.城镇与农村储户一次存(取)款金额的分析比较 利用居民储蓄调查数据计算存(取)款金额的基本描述统计量,并对城镇储户 和农村储户进行比较。 首先按照户口对数据进行拆分(SplitFile),然后计算存(取)款金额的基本 描述统计量,SPSS操作结果如表1所示。 表1城镇储户和农村储户存(取)款金额的基本描述统计量 Descriptive Statistics 户口 城镇户口 农村户可 存(取)款alid 存(取)款金额alid listwise) Statistic 22% 223 90 ang Statistic 5024 80501l Statistic Statistic 3025 80502 Statistic 2687.2 194.97 Std.Deviation Statistic 5737.566 8816.360 kewness Statistic 4.57 8.31 Std.Error .16 .254 rtosis 26.9 713 Std.Error .324 .503 表1表明,城镇储户的一次平均存(取)款金额(2687.2元)高于农村储户 (1944.97元)。标准差证明了城镇储户存(取)款金额的离散程度低于农村储户
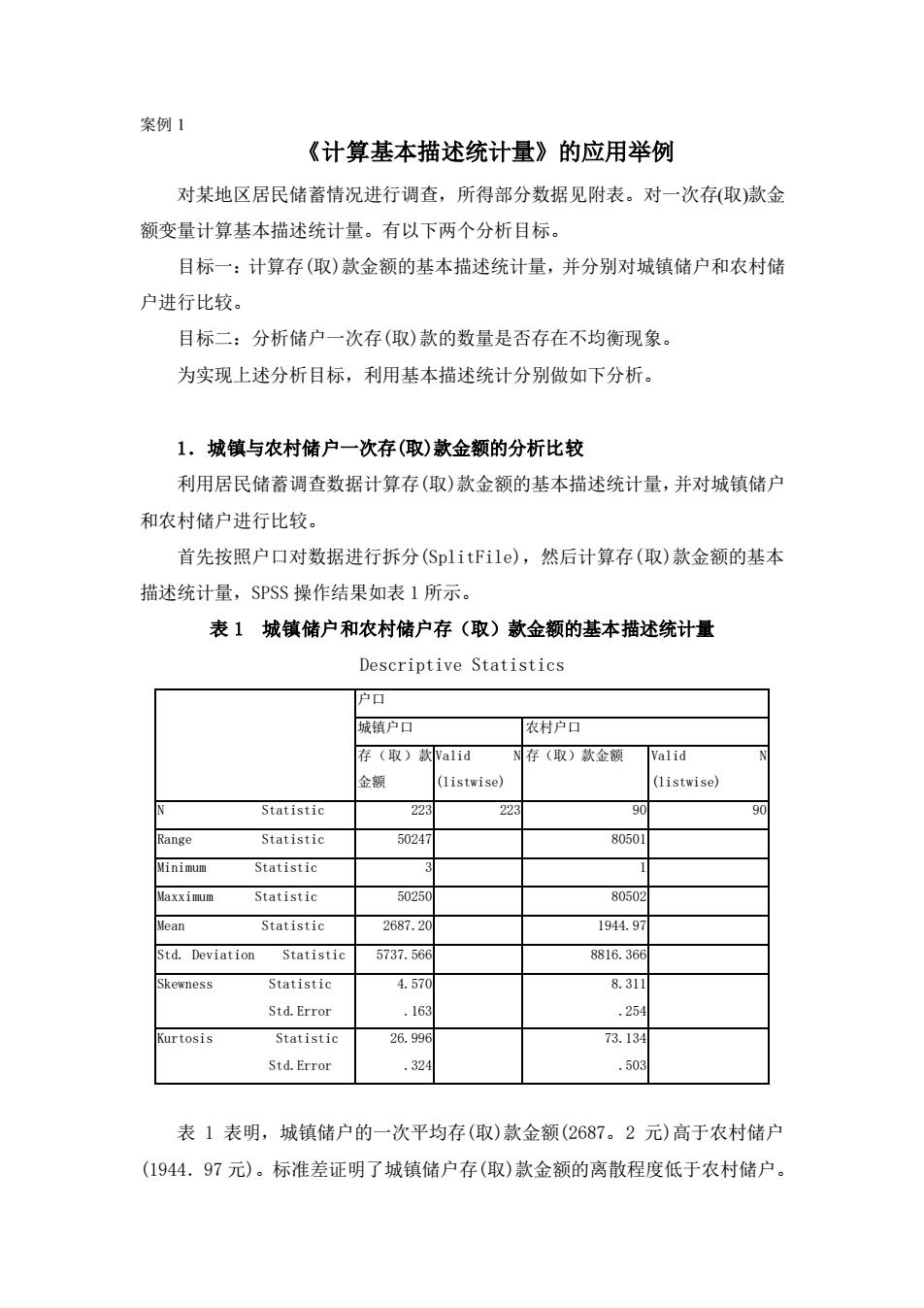
案例 1 《计算基本描述统计量》的应用举例 对某地区居民储蓄情况进行调查,所得部分数据见附表。对一次存(取)款金 额变量计算基本描述统计量。有以下两个分析目标。 目标一:计算存(取)款金额的基本描述统计量,并分别对城镇储户和农村储 户进行比较。 目标二:分析储户一次存(取)款的数量是否存在不均衡现象。 为实现上述分析目标,利用基本描述统计分别做如下分析。 1.城镇与农村储户一次存(取)款金额的分析比较 利用居民储蓄调查数据计算存(取)款金额的基本描述统计量,并对城镇储户 和农村储户进行比较。 首先按照户口对数据进行拆分(SplitFile),然后计算存(取)款金额的基本 描述统计量,SPSS 操作结果如表 1 所示。 表 1 城镇储户和农村储户存(取)款金额的基本描述统计量 Descriptive Statistics 户口 城镇户口 农村户口 存(取)款 金额 Valid N (listwise) 存(取)款金额 Valid N (listwise) N Statistic 223 223 90 90 Range Statistic 50247 80501 Minimum Statistic 3 1 Maxximum Statistic 50250 80502 Mean Statistic 2687.20 1944.97 Std. Deviation Statistic 5737.566 8816.366 Skewness Statistic Std.Error 4.570 .163 8.311 .254 Kurtosis Statistic Std.Error 26.996 .324 73.134 .503 表 1 表明,城镇储户的一次平均存(取)款金额(2687。2 元)高于农村储户 (1944.97 元)。标准差证明了城镇储户存(取)款金额的离散程度低于农村储户

无论城镇储户还是农村储户,存(取)款金额的分布均呈右偏分布(两个偏度统计 量分别为4.57和8.311),且农村的偏斜程度更大些(8.311>4.57):同时 城镇储户和农村储户存(取)款金额均呈尖峰分布(两个峰度统计量分别为 26.996和?3.134),且农村更尖峰。由此可见,城镇储户和农村储户中的大部 分人一次存(取)款金额都低于平均水平,且农村储户表现得更为明显。 2.储户一次存{取)款数量的均衡性分析 分析储户一次存(取)款数量是否存在不均衡现象,可以从分析金额是否有大 量异常值人手。这里,如果假设储户一次存<取)款金额的分布服从正态分析,那 么根据3,准则,异常值通常为3个标准差之外的变量值,可通过对数据的标准 化处理来判断。 标准化的数学定义为: Z=(x-x)/S (4.1) 通过标准化可得到一系列新变量值,通常称为标准化值或Z分数。由式(4.1) 可见,标准化值反映的是变量值与变量均值的差是几个标准差单位。如果标准化 值等于0(即分子为0),则表示该变量值等于变量均值:如果标准化值大于0(即 分子为正),则表示该变量值大于变量均值:如果标准化值小于。(即分子为负), 则表示该变量值小于变量均值。 基于上述对案例申存(取)款金额数据分布的假设和分析的要求,计算存(取) 款金额的标准化值。SPSS可计算存(取)款金额的标准化值并将结果保存在一个 新变量Za中。对该变量的取值进行分组整理,可以发现乙分数值的绝对值大于 3的储户是存在的。对变量分组为三组(亿a<=-36低金额组、-36<Za<36中金额组、 Z>3ó高金额组)后进行频数分析可得,低金额组(即低异常值组)的比例为0%, 高金额组<即高异常值组)的比例为2.2%。异常组的总比例大于理论值0.3%, 因此可以认为存(取)款金额存在一定的不均衡现象。 附表 居民储蓄调查数据表
无论城镇储户还是农村储户,存(取)款金额的分布均呈右偏分布(两个偏度统计 量分别为 4.57 和 8。311),且农村的偏斜程度更大些(8.311>4.57);同时, 城镇储户和农村储户存(取)款金额均呈尖峰分布(两个峰度统计量分别为 26.996 和?3。134),且农村更尖峰。由此可见,城镇储户和农村储户中的大部 分人一次存(取)款金额都低于平均水平,且农村储户表现得更为明显。 2.储户一次存{取)款数量的均衡性分析 分析储户一次存(取)款数量是否存在不均衡现象,可以从分析金额是否有大 量异常值人手。这里,如果假设储户一次存<取)款金额的分布服从正态分析,那 么根据 3,准则,异常值通常为 3 个标准差之外的变量值,可通过对数据的标准 化处理来判断。 标准化的数学定义为: Zi=( xi- xi)/S (4.1) 通过标准化可得到一系列新变量值,通常称为标准化值或 Z 分数。由式(4.1) 可见,标准化值反映的是变量值与变量均值的差是几个标准差单位。如果标准化 值等于 0(即分子为 0),则表示该变量值等于变量均值;如果标准化值大于 0(即 分子为正),则表示该变量值大于变量均值;如果标准化值小于 o(即分子为负), 则表示该变量值小于变量均值。 基于上述对案例申存(取)款金额数据分布的假设和分析的要求,计算存(取) 款金额的标准化值。 SPSS 可计算存(取)款金额的标准化值并将结果保存在一个 新变量 Za 中。对该变量的取值进行分组整理,可以发现 Z 分数值的绝对值大于 3 的储户是存在的。对变量分组为三组(Za<=-3ó低金额组、-3ó<Za<3ó中金额组、 Za>3ó高金额组)后进行频数分析可得,低金额组 (即低异常值组)的比例为 0%, 高金额组<即高异常值组)的比例为 2.2%。异常组的总比例大于理论值 0.3%, 因此可以认为存(取)款金额存在一定的不均衡现象。 附表 居民储蓄调查数据表
存取款金户口(城镇存取款户口(城镇存 取款户口(城花取款户口(城镇 额(元) ,农村=2 农村=2 农村=2) (元) 农村=) 1500 3700 7000 100 5000 100 200 10000 200 100 10000 2500 1000 300 300 3500 600 500 10 18000 100 500 3200 100 2000 480 50 1000 5000 400 100 200 2400 0 200 5 14800 10 200 500 25000 6000 100 100 100 100 300 1000 500 100 3 200 10000 30 50 200 400 200 148 5400 800 10 3 5000 10 3000 500 8000 0 200 500 23900 100 1000 200 1100 500 3268 5000 100 7000 1000 10000 800 g00 50 500 500 1000 1000 1000 3 3000 500 600 00 1000 3 10 20 1200 1000 000 1000 10 900 1200 5000 350 100 2000 10000 20a 3600 300 500 200 1000 500 700
存取款金 额(元) 户口(城镇= 1,农村=2) 存取款金 额(元) 户口(城镇= 1,农村=2) 存取款金 额(元) 户口(城镇= 1,农村=2) 存取款金 额(元) 户口(城镇= 1,农村=2) 1500 1 3700 1 7000 1 100 1 5000 1 100 2 200 1 10000 1 200 1 100 1 10000 1 2500 1 1000 1 300 1 300 1 3500 1 300 1 600 2 300 1 3 1 6500 1 500 1 2000 1 10 1 18000 1 100 1 500 1 8 1 3200 1 100 1 2000 1 20 1 480 1 50 1 1000 1 5000 1 400 1 100 1 200 1 2400 1 300 1 200 1 5000 1 14800 1 10 1 200 1 500 1 25000 1 6000 1 100 1 100 1 100 1 100 1 300 1 1000 1 5000 1 500 1 100 1 3 1 200 1 1000 1 10000 1 2000 1 30 1 10 1 500 1 300 1 1000 1 200 2 400 1 300 1 200 2 6 1 148 1 5400 1 800 2 10 1 3 1 300 1 40 2 5000 1 10 1 3000 1 500 2 8000 1 150 1 20000 1 60 2 300 2 500 1 23900 2 100 2 1000 1 200 1 1100 1 500 2 3268 2 5000 1 100 1 1000 2 7000 1 1000 1 10000 1 800 2 800 1 50 1 500 1 500 2 1000 1 1000 1 5000 1 400 2 1000 1 3 1 3000 1 200 2 500 1 600 1 30000 1 3000 2 1000 1 3 1 5000 1 1000 2 20 1 1200 2 1000 1 5000 2 3 1 1000 1 4600 1 10 2 5 1 900 1 2000 2 8 2 1200 1 5000 1 350 1 50 2 100 1 2000 1 1000 1 10 2 500 1 10000 1 1000 1 5 2 300 1 3600 1 300 1 500 2 200 1 1000 1 500 1 700 2
300 300 3500 50 600 200 1000 500 800 30 100 8000 3000 1000 00 500 00 1000 900 30 30000 100 00 2000 600 800 900 1500 200 300 980 1500 1000 1000 500 2 25000 500 1000 1000 80502 1000 3000 2 1000 200 100 1000 8 1000 20000 2000 100 2 90 600 1000 800 10000d 400 100 20 70 90 50250 5500 150 10000 5500 700 3000 1500 1000 700 2000 3 500 100 5000 1000 200 100 1500 10 1000 4000 500 60 1200 00 10 500 100 700 15000 1300 100 260 4500 200 5000 1500 00 500 20 100 1000 500 600 00 20 2000 5000 100 1000 30 用》 电子 7年4月
300 1 300 1 3500 1 50 2 600 2 200 1 1000 1 5 1 1000 1 500 1 200 1 800 2 30 1 1000 1 1000 1 2 2 8000 1 3000 1 1000 1 9 2 900 1 500 1 5000 1 14 2 1000 1 900 1 3000 1 1000 2 30000 1 100 1 200 1 2000 2 600 1 800 1 900 1 1500 2 200 1 300 1 60 2 980 2 1500 1 1000 2 1000 2 500 2 7000 1 25000 1 1000 2 500 2 1000 1 1000 1 10000 2 1000 2 80502 2 1000 1 3000 2 5 2 3 1 1000 1 200 2 5 2 100 1 1000 1 120 2 8 2 1000 1 20000 1 800 2 6 2 3 1 2000 1 100 2 110 2 90 1 600 2 1000 2 800 2 800 1 10000 1 400 2 1 2 1000 1 20 1 70 2 100 2 90 2 50250 1 1 2 60 2 1000 1 5500 1 400 2 1000 2 1700 1 1500 2 900 2 700 2 10000 1 5500 1 700 2 3000 2 100 1 1500 1 1000 1 700 2 500 1 2000 1 3000 1 500 2 100 1 5000 1 1000 1 200 2 1000 1 1500 1 10 1 1000 2 4000 1 500 1 600 1 1200 2 80 1 200 1 10 1 500 2 100 1 700 1 15000 1 1300 2 100 1 260 1 4500 1 200 2 100 1 5000 1 1500 1 1100 2 200 1 5000 1 500 1 2000 2 100 1 1000 1 500 1 600 2 200 1 3 2 500 2 100 2 400 1 200 1 200 1 2000 1 5000 1 100 1 1000 1 2000 1 3000 1 资料来源:薛薇,《SPSS 统计分析方法及应用》,电子工业出版社,2007 年 4 月