
图3.16带摇摆柱的多跨刚 =4,h 式(3-9) 式中:4一—刚架边柱的计算长度系数,由表34查得,但式(3-8)中的s取与边柱相连 的一跨横梁的坡面长度人,参见图3.16: 7一—放大系数,刀= 摆柱承受的荷载 P 刚架 承受的荷载: 摇摆柱高度: 一—刚架边柱高度。 费的整适用于度不大于15的情,超过此值时应考电 梁轴向力对柱刚度的不利影响。 (3)对于带此屋的则架,可近似的将毗屋柱视为摇摆柱,此时主则架样的计算长度系 数4可由表34查得,并应乘以放大系数。计算刀时,乃为毗屋柱承受的竖向荷载,为 刚架柱承受的荷载。 马聚利酒产价分折计草程学得出柱原木平荷我作用下的测移附度K:心(见图 3.17)时,柱计算长度系数可按下列式子计算: (1)单跨对称刚架 当柱脚较接时 4=44 式(3.10) 当柱脚刚接时 4-5 式(3-11) 式中:h一一柱的高度。 (a)单跨对称刚架 (b)多骑刚架 图3.17一阶分析时的顶侧移
16 图 3.16 带摇摆柱的多跨刚架 h0 =rh 式(3-9) 式中: r ——刚架边柱的计算长度系数,由表 3-4 查得,但式(3-8)中的 s 取与边柱相连 的一跨横梁的坡面长度 b l ,参见图 3.16; ——放大系数, = + h i P h P f fi li li 1 ; Pli ——摇摆柱承受的荷载; Pfi ——刚架边柱承受的荷载; hli ——摇摆柱高度; hfi ——刚架边柱高度。 摇摆柱的计算长度系数 r =1.0 。 上述分析中,计算长度系数 r 适用于屋面坡度不大于 1:5 的情况,超过此值时应考虑横 梁轴向力对柱刚度的不利影响。 (3)对于带毗屋的刚架,可近似的将毗屋柱视为摇摆柱,此时主刚架柱的计算长度系 数 r 可由表 3-4 查得,并应乘以放大系数 。计算 时, Pl 为毗屋柱承受的竖向荷载, Pf 为 刚架柱承受的荷载。 2. 一阶分析法 当刚架利用一阶分析计算程序得出柱顶水平荷载作用下的侧移刚度 K = H u (见图 3.17)时,柱计算长度系数可按下列式子计算: (1)单跨对称刚架 当柱脚铰接时 Kh EIc0 r = 4.14 式(3-10) 当柱脚刚接时 3 c0 r 5.85 Kh EI = 式(3-11) 式中:h——柱的高度。 (a)单跨对称刚架 (b)多跨刚架 图 3.17 一阶分析时的柱顶侧移

(2)中间为摇摆柱的多跨对称刚架 当屋面坡度不大于1:5时,边柱计算长度系数4仍按式(3-10)或式(3-11)计算,但 须乘以放大系数n=1+∑BA)12∑):摇摆柱的计算长度系数4取1.0。 (3)中间为非摇摆柱的多跨刚架 当柱脚为铰接时 4-05侵份Σ会 式(3-12) 当柱脚刚接时 4=12骨Σ 式(3-13) -提 式(3-14) 式中:h,一一第1根柱的高度: P一一第1根柱的竖向荷载: :一一第/根柱的以小头为准的参数 3.二阶分析法 采用计入竖向荷载侧移效应(P4效应)的二阶分析程序计算内力时,计算长度系数4 可按下列式子计算: 4=1-0.375r+0.08y20-0.0775) 式(3-15) 式(3-16) do 式中:y一一构件楔率,不大于0.268h/d及6.0: d、山一一构件小头、大头的截面高度,如图3.18所示 刚架柱在刚架平面外的计算长度,取侧向支撑点间的距离。当柱两边缘侧向支撑点间 离不等时,应取最大受压边缘侧向支撑点间的距离。 图3.18变截面构件的搜率 3.5.4变截面刚架梁、柱的弹性设计 一、刚架梁、柱板件魔厚比限值 刚架梁、 柱通常采用如图3.19所示的工字形截面,其受压翼缘板宽厚比限值为: 式(3-17)
17 (2)中间为摇摆柱的多跨对称刚架 当屋面坡度不大于 1:5 时,边柱计算长度系数 r 仍按式(3-10)或式(3-11)计算,但 须乘以放大系数 = +( ) ( ) li li fi fi ' 1 P h 1.2 P h ;摇摆柱的计算长度系数 r 取 1.0。 (3)中间为非摇摆柱的多跨刚架 当柱脚为铰接时 = i i i ' E0i r 1.2 0.85 h P P P K 式(3-12) 当柱脚刚接时 = i i i ' E0i r 1.2 1.2 h P P P K 式(3-13) 2 i c0 2 ' E0i h EI P = 式(3-14) 式中: i h ——第 i 根柱的高度; Pi ——第 i 根柱的竖向荷载; ' PE0i——第 i 根柱的以小头为准的参数。 3. 二阶分析法 采用计入竖向荷载-侧移效应(P-效应)的二阶分析程序计算内力时,计算长度系数 r 可按下列式子计算: 1 0.375 0.08 (1 0.0775 ) 2 r = − + − 式(3-15) 0 1 d d = 式(3-16) 式中: ——构件楔率,不大于 268 0 0. h d 及 6.0; d0 、 d1——构件小头、大头的截面高度,如图 3.18 所示。 刚架柱在刚架平面外的计算长度,取侧向支撑点间的距离。当柱两边缘侧向支撑点间距 离不等时,应取最大受压边缘侧向支撑点间的距离。 图 3.18 变截面构件的楔率 3.5.4 变截面刚架梁、柱的弹性设计 一、刚架梁、柱板件宽厚比限值 刚架梁、柱通常采用如图 3.19 所示的工字形截面,其受压翼缘板宽厚比限值为: t b1 ≤ y 235 15 f 式(3-17)
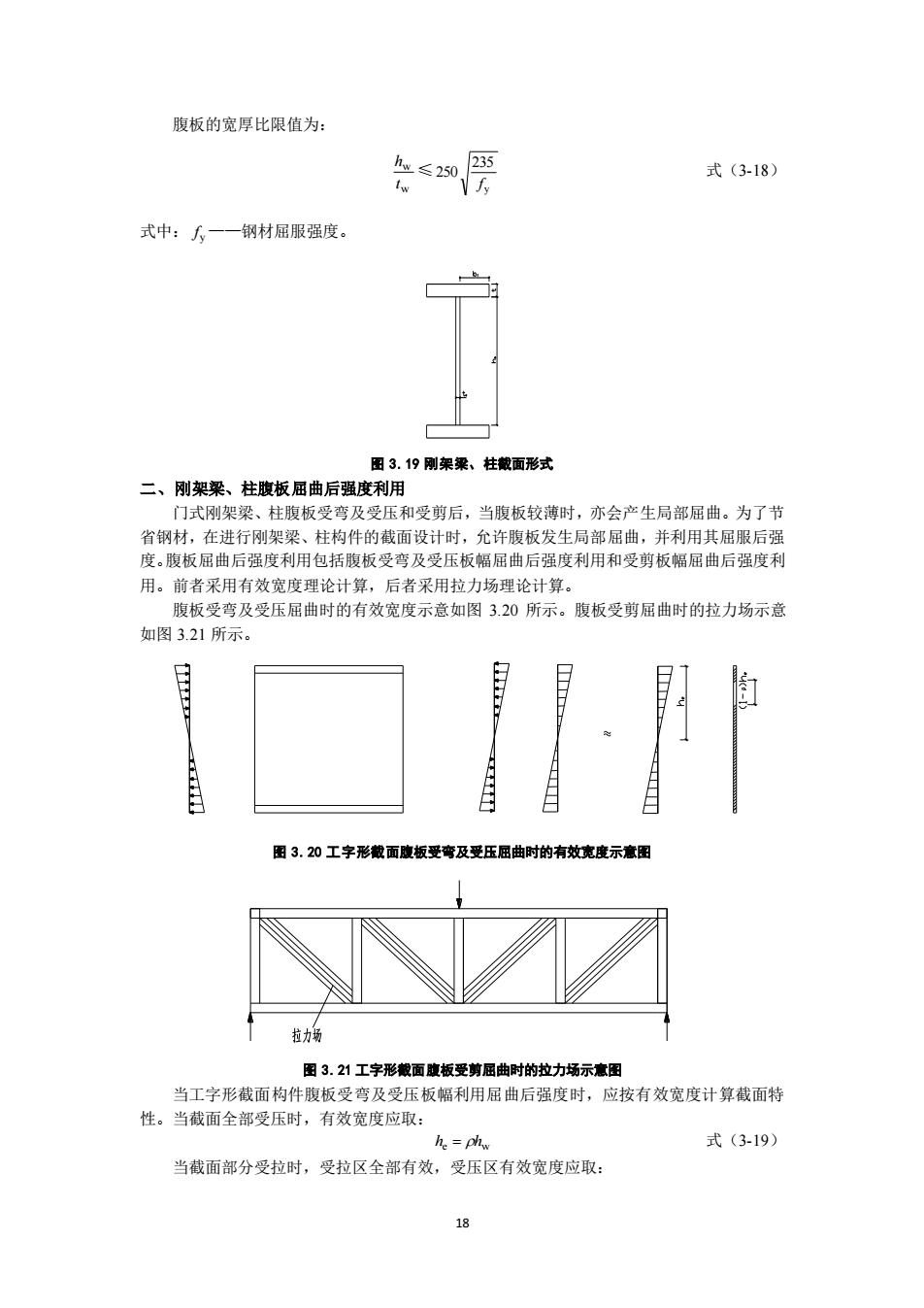
腹板的宽厚比限值为: 式(3-18) 式中:人一一钢材屈服强度。 图3.19刚架梁、柱戴面形式 二、刚架梁、柱腹板屈曲后强度利用 门式刚架梁、柱腹板受弯及受压和受剪后,当腹板较薄时,亦会产生局部屈曲。为了节 省钢材,在进行刚架梁、柱构件的截面设计时,允许腹板发生局部屈曲,并利用其屈服后强 度。腹板屈曲后强度利用包括腹板受弯及受压板幅屈曲后强度利用和受剪板幅屈曲后强度利 用。前者采用有效宽度理论计算,后者采用拉力场理论计算。 腹板受弯及受压屈曲时的有效宽度示意如图320所示。腹板受剪屈曲时的拉力场示意 如图3.21所示。 图3.20工字形截面腹板受弯及受压屈曲时的有效宽度示意图 拉力 图3.21工字形面腹板受剪屈曲时的拉力场示意围 当工字形截面构件腹板受弯及受压板幅利用屈曲后强度时,应按有效宽度计算截面特 性。当截面全部受压时,有效宽度应取: h.ch 式(3-19) 当截面部分受拉时,受拉区全部有效,受压区有效宽度应取:
18 腹板的宽厚比限值为: w w t h ≤ y 235 250 f 式(3-18) 式中: y f ——钢材屈服强度。 图 3.19 刚架梁、柱截面形式 二、刚架梁、柱腹板屈曲后强度利用 门式刚架梁、柱腹板受弯及受压和受剪后,当腹板较薄时,亦会产生局部屈曲。为了节 省钢材,在进行刚架梁、柱构件的截面设计时,允许腹板发生局部屈曲,并利用其屈服后强 度。腹板屈曲后强度利用包括腹板受弯及受压板幅屈曲后强度利用和受剪板幅屈曲后强度利 用。前者采用有效宽度理论计算,后者采用拉力场理论计算。 腹板受弯及受压屈曲时的有效宽度示意如图 3.20 所示。腹板受剪屈曲时的拉力场示意 如图 3.21 所示。 图 3.20 工字形截面腹板受弯及受压屈曲时的有效宽度示意图 图 3.21 工字形截面腹板受剪屈曲时的拉力场示意图 当工字形截面构件腹板受弯及受压板幅利用屈曲后强度时,应按有效宽度计算截面特 性。当截面全部受压时,有效宽度应取: he = hw 式(3-19) 当截面部分受拉时,受拉区全部有效,受压区有效宽度应取:
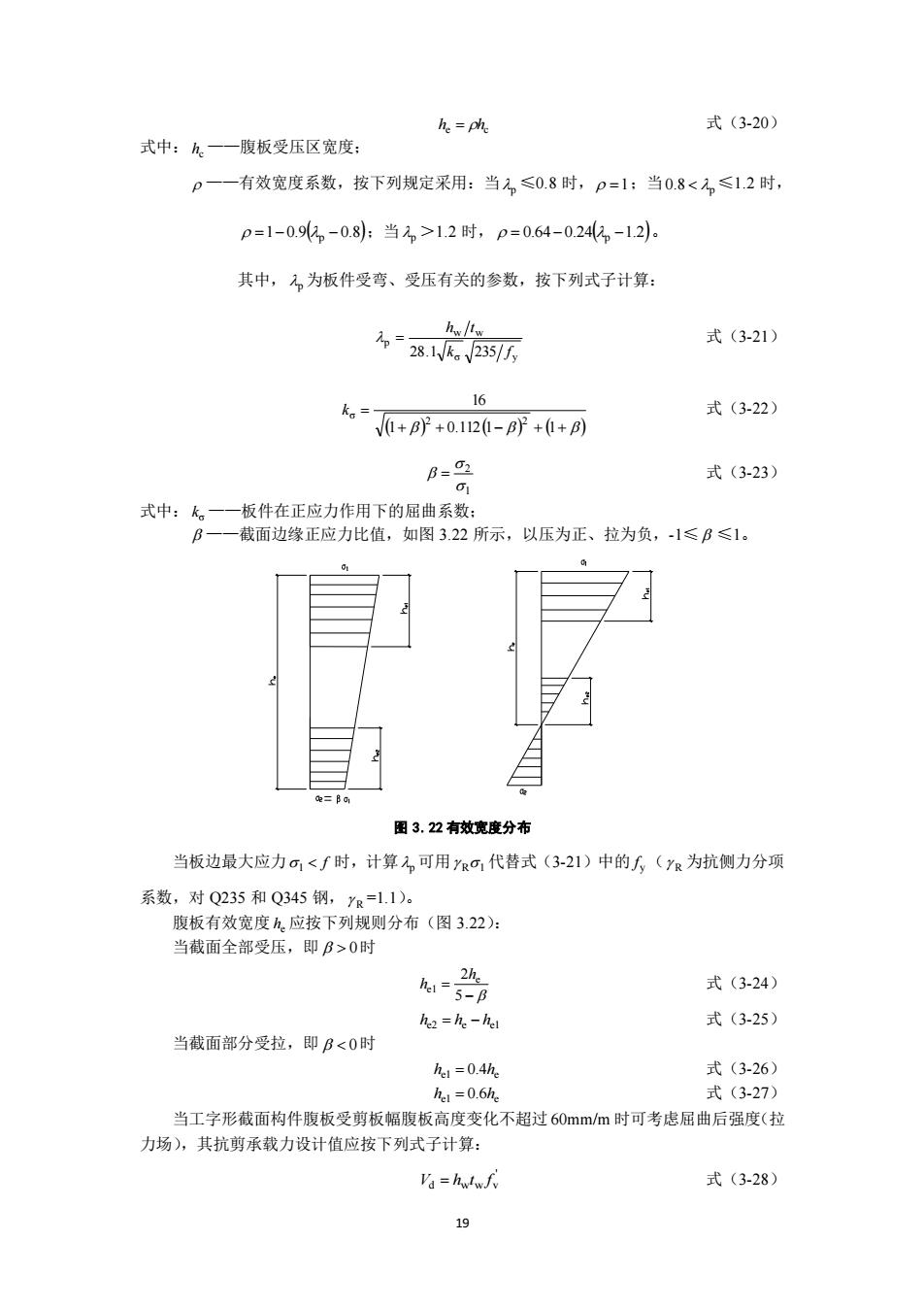
he phe 式(3-20) 式中:A一—腹板受压区宽度: p一一有效宽度系数,按下列规定采用:当,≤0.8时,p=1:当0.8<2,≤12时, p=1-0.91。-0.8:当1,>1.2时,p=0.64-0.243-12。 其中,不,为板件受弯、受压有关的参数,按下列式子计算: 式(3-21) 16 k。0+Br+0120-p㎡+0+例 式(3-22) B=2 式(3-23) 式中:k。一一板件在正应力作用下的屈曲系数: B一一截面边缘正应力比值,如图3.22所示,以压为正、拉为负,-1≤B≤1。 图3.2有效宽度分布 当板边最大应力c<∫时,计算,可用,代替式(3-21)中的(为抗侧力分项 系数,对Q235和Q345钢,yR=1.1)。 腹板有效宽度h.应按下列规则分布(图3.22): 当截面全部受压,即B>0时 式(3-24) he =he hel 式(3-25) 当截面部分受拉,即B<0时 式(3-26) 式(3.27) 当工字形截面构件腹板受剪板幅腹板高度变化不超过60mm/m时可考虑屈曲后强度(拉 力场),其抗剪承载力设计值应按下列式子计算: Va hwtwfy 式(3-28)
19 he = hc 式(3-20) 式中: hc ——腹板受压区宽度; ——有效宽度系数,按下列规定采用:当 p ≤0.8 时, =1 ;当 8 p 0. ≤1.2 时, 1 0.9( 0.8) = − p − ;当 p >1.2 时, 0.64 0.24( 1.2) = − p − 。 其中, p 为板件受弯、受压有关的参数,按下列式子计算: σ y w w p 28.1 k 235 f h t = 式(3-21) ( + ) + ( − ) + ( + ) = 1 0.112 1 1 16 2 2 σ k 式(3-22) 1 2 = 式(3-23) 式中: σ k ——板件在正应力作用下的屈曲系数; ——截面边缘正应力比值,如图 3.22 所示,以压为正、拉为负,-1≤ ≤1。 图 3.22 有效宽度分布 当板边最大应力 f 1 时,计算 p 可用 R1 代替式(3-21)中的 y f ( R 为抗侧力分项 系数,对 Q235 和 Q345 钢, R =1.1)。 腹板有效宽度 he 应按下列规则分布(图 3.22): 当截面全部受压,即 0 时 − = 5 2 e e1 h h 式(3-24) he2 = he − he1 式(3-25) 当截面部分受拉,即 0 时 e1 4 e h = 0. h 式(3-26) e1 6 e h = 0. h 式(3-27) 当工字形截面构件腹板受剪板幅腹板高度变化不超过 60mm/m 时可考虑屈曲后强度(拉 力场),其抗剪承载力设计值应按下列式子计算: ' d w w v V = h t f 式(3-28)

当元≤0.8时 =人 式(3-29 当0.8<<14时 =[-0.64久-0.8 式(3-30) 当元≥1.4时 f=1-0.2751) 式(3-31) 式中:人一一钢材抗剪强度设计值: h一一腹板高度,对楔形腹板取板幅平均高度: 广一一腹板屈曲后抗剪强度设计值: 入一与板件受剪有关的参数,按下列公式计算: w= 式(3-32) 当ah≤1时 =4+534 式(3-33) 当ah≥1时 =534+ 式(3-34) 式中:k,一一受剪板件的屈曲系数,当不设横向加劲肋时,取k=534: 一横线加劲肋间距,当利用腹板屈曲后抗剪强度时,宜取a=~2h。 三、刚架构件的强度计算 L,工字形截面受弯构件在剪力V和弯矩M共同作用下的强度,应符合下列要求: 当V≤0.5a时 M≤M. 式(3-35) 当0.5a<P≤时 式(3-36) 当截面为双轴对称时 M:=4伍w+/ 式(3-37) 式中:M 两翼缘所承担的弯矩 M。一一构件有效截面所承担的弯矩,M从。=形。f: W。一一构件有效截面最大受压纤维的截面模量: 4一一构件翼缘的截面面积:
20 当 w ≤0.8 时 v ' v f = f 式(3-29) 当 0.8< w <1.4 时 ( ) w v ' fv = 1− 0.64 − 0.8 f 式(3-30) 当 w ≥1.4 时 ( ) w v ' fv = 1− 0.275 f 式(3-31) 式中: v f ——钢材抗剪强度设计值; hw ——腹板高度,对楔形腹板取板幅平均高度; ' v f ——腹板屈曲后抗剪强度设计值; w ——与板件受剪有关的参数,按下列公式计算: y τ w w w 235 37 f k t h = 式(3-32) 当 a hw ≤1 时 2 w τ 5.34 4 = + h a k 式(3-33) 当 a hw ≥1 时 2 w τ 4 5.34 = + h a k 式(3-34) 式中: τ k ——受剪板件的屈曲系数,当不设横向加劲肋时,取 kτ = 5.34 ; a ——横线加劲肋间距,当利用腹板屈曲后抗剪强度时,宜取 a = (1~ 2)hw 。 三、刚架构件的强度计算 1. 工字形截面受弯构件在剪力 V 和弯矩 M 共同作用下的强度,应符合下列要求: 当 V ≤ 5 d 0. V 时 M ≤ Me 式(3-35) 当 5 d 0. V < V ≤ Vd 时 M ≤ ( ) + − − − 2 d f e f 1 0.5 1 V V M M M 式(3-36) 当截面为双轴对称时 M = A (hw + t)f f f 式(3-37) 式中: Mf ——两翼缘所承担的弯矩; Me ——构件有效截面所承担的弯矩, M W f e = e ; We——构件有效截面最大受压纤维的截面模量; Af ——构件翼缘的截面面积;