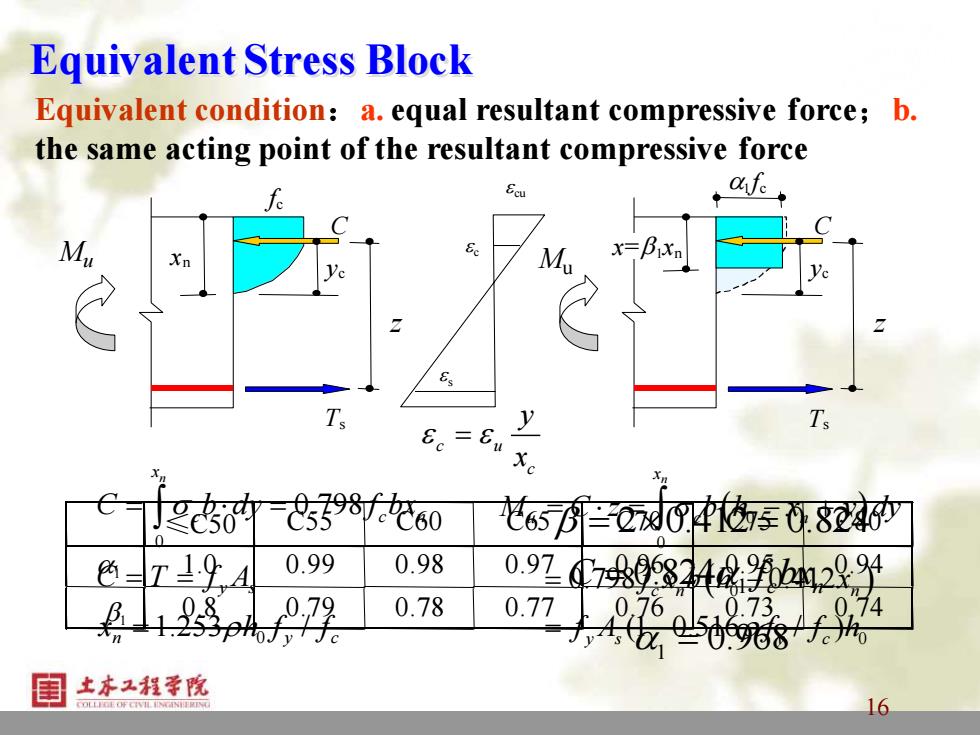
Equivalent Stress Block Equivalent condition:a.equal resultant compressive force;b. the same acting point of the resultant compressive force f x= 3.x 6e=u Xn Cd5398f60 花650048每0824 0.99 0.98 0.97709841294 0.78 0.77 土本工程学院 16
16 16 Equivalent Stress Block ( ) ( ) 0 0 0 0 0.798 0.412 (1 0.516 / ) n x u c n c n n y s y c M C z b h x y dy f x b h x f A f f h = = − + = − = − 0 0 0.798 1.253 / n x c c n y s n y c C b dy f bx C T f A x h f f = = = = = a1 C Ts z Mu fc yc x=b1xn Equivalent condition:a. equal resultant compressive force;b. the same acting point of the resultant compressive force e cu C Ts z fc xn yc Mu es e c c u c y x e e = b = = 2 0.412 0.824 1 0.824 C f bx = a c n 1 a = 0.968 ≤C50 C55 C60 C65 C70 C75 C80 a1 1.0 0.99 0.98 0.97 0.96 0.95 0.94 b1 0.8 0.79 0.78 0.77 0.76 0.73 0.74

Balanced Section Balanced section is defined as a section that will fail with the tension steel yielding and,simultaneously Sothe extreme compFessiVETSMGR iH comrereqeefes 0.0933 h Stress fhe-thdhen firesthe Aanced rehto concrete surrounding the acting point ement cu 0,= for undereiprced beam 0.002 Over-reiforcement u 秋cmfn,E, 5u,。+6 afc 55子52号之Under-rforced beam py pO 5=50r5,书5 Blancg reinforeed beam 5>560r5n>5b Over-reinforced beam 目土本工程幸院 17
17 17 Balanced Section Balanced section is defined as a section that will fail with the tension steel yielding and simultaneously the extreme compressive strain in concrete reaches 0.0033. e cu e y xnb h0 Balanced reinforcement Under-reinforcement Over-reinforcement 0 nb cu cu y x h e e e = + 0 h xb b = 1 0 nb x h b = cu y cu e e b e + = 1 1 cu y cu b e e b e + = cu s y E f e b + = 1 1 0 x h = 1 0 0, for under-reinforced beam c s s s y N f b h A f a = = = c s y c y f f bh A f f 1 0 a1 a = = a1 C Ts z Mu fc yc x=b1xn b n nb or Under-reinforced beam = = b n nb or b n nb or Over-reinforced beam Balanced reinforced beam s p y p cu b cu E h f x 1 0 0 e e b − + = 1 0 0 1 b b py p cu s x h f E b e = = − + 0 0 n cu py p cu s x h f E e e = − + p0 e py e xn ecu 0 Stress increment till steel yielding: py p f − Stress in the tendon when stress in the concrete surrounding the acting point of resultant prestresing force is zero 0.002 fpy e e py =0.002+fpy/Es py py Es e = 0.002 + f 1 0.002 0 1 b py p cu cu s f E b e e = − + +

Basic Equations for Ultimate Limit State ∑N=0,afbx=f,A ∑M=0,M≤M,=4fh-之=人,Ah,-2 a 5= f,A aifbho 三Ps C=abx xf。 x=Bixn Mu (ho-x/2) M.=afb(1-0.55)=a,a f.bh =fAh(1-0.55)=Af,yh T=fyAs 土本工程学晚 18
18 18 Basic Equations for Ultimate Limit State 1 1 0 0 0, 0, ( ) ( ) 2 2 c y s u c y s N f bx f A x x M M M f bx h f A h a a = = = = − = − C=a1fcbx T =f yAs Mu a1fc x=b1xn (h0 -x/2) c y s c y s f f f bh f A h x 0 1 0 a1 a = = = 2 2 1 0 1 0 0 0 (1 0.5 (1 0.5 ) ) u c s c y s y s s M f bh f bh f A h A f h a a a − = = = − =

Applicable Conditions P≤Pmax x≤56h0r5≤5b M≤a&mafbh M=0.322fbh,2 p≥Pmin M,*f,4-3)人4×09% Pun =0.451 =4=0.36 bho f 目土本工程幸院 19
19 19 max Applicable Conditions 0 b b x h or 2 M f bh a a s c max 1 0 xn xn /3 fyAs Mu C h0 min 0 9 0 ) 0. 3 ( f A h x M f A h y s n y y s − 2 0 0.322 M f bh cr t = y s t f f bh A 0.36 0 min = = y t f f min = 0.45

Doubly Reinforced Section (DRS) When to use DRS? Restriction on dimensions of the cross section ho Moment on the cross h section changes the sign 土本工程学院 20
20 Doubly Reinforced Section (DRS) When to use DRS? Restriction on dimensions of the cross section Moment on the cross section changes the sign b h0 h 20