
Advanced Theory of Concrete Structures Chapter 5 Shearing Behavior of Reinforced Concrete Structural Members Yong Zhou College of Civil Engineering,Tongji University 目 土本工程学院 yongzhou@tongji.edu.cn COLLEGEOF CNVIL INGINELRIM
Yong Zhou College of Civil Engineering, Tongji University yongzhou@tongji.edu.cn Chapter 5 Shearing Behavior of Reinforced Concrete Structural Members Advanced Theory of Concrete Structures
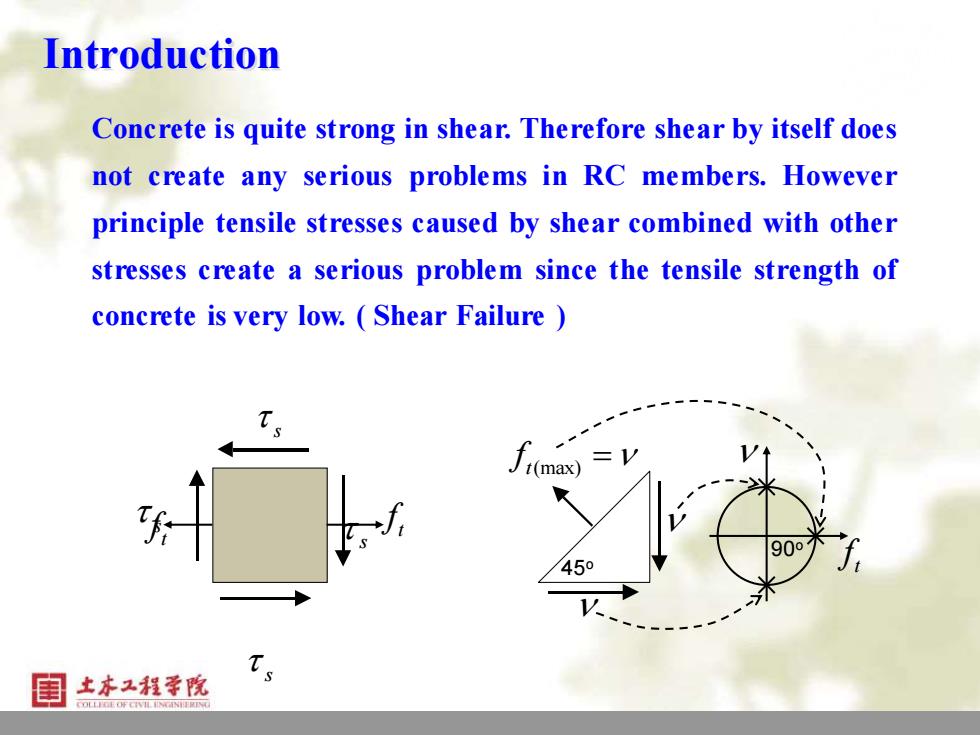
Introduction Concrete is quite strong in shear.Therefore shear by itself does not create any serious problems in RC members.However principle tensile stresses caused by shear combined with other stresses create a serious problem since the tensile strength of concrete is very low.Shear Failure t(max 90 4 目土本工程幸院
2 Introduction Concrete is quite strong in shear. Therefore shear by itself does not create any serious problems in RC members. However principle tensile stresses caused by shear combined with other stresses create a serious problem since the tensile strength of concrete is very low. ( Shear Failure ) 45o t(max) f = t f 90o s s s t f t f s

Introduction Characteristics of shear failure Abrupt without sufficient warning. Damage in shear tends to be more localized than in bending, i.e.,width of crack in shear is wider than in bending The nature of shear failure is very brittle.So it can result in catastrophic disaster if it is not properly designed. 土本工程学脱
3 Introduction ◼ Characteristics of shear failure ◼Abrupt without sufficient warning. ◼Damage in shear tends to be more localized than in bending, i.e., width of crack in shear is wider than in bending. ◼The nature of shear failure is very brittle. So it can result in catastrophic disaster if it is not properly designed

Shear Stress in an Uncracked Elastic Beam NMINIHIMINMMNIMIRmMMMNII R T-Sodd-fMdM Shear forces dT dMo T+dT-T=bvdx bl dT dMo Vo 1y= Section Beam Flexural Shear Shear dx dxbI bI element stresses flow stresses 目 土本工程学院
4 Shear Stress in an Uncracked Elastic Beam d d d My T A A I M MQ y A I I dMQ dT I = = = = = dT dM Q VQ v dx dxbI bI = = = T dT T bvdx + − =
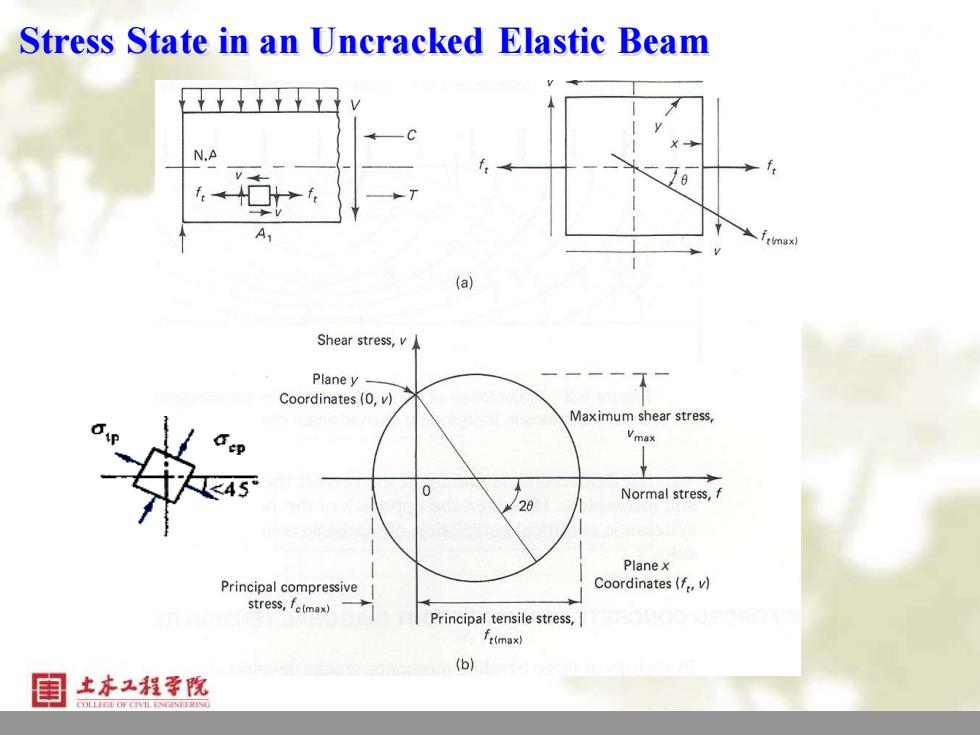
Stress State in an Uncracked Elastic Beam ax (a) Shear stress,v Plane y Coordinates(0,v) Maximum shear stress, 45 Normal stress,f 28 Plane x Principal compressive Coordinates (f,v) stress,fe(max) Principal tensile stress, t(max) (b) 土本工程学院
5 Stress State in an Uncracked Elastic Beam