
Public Key Cryptography symmetric key crypto: public key crypto requires sender,receiver radically different approach know shared secret key [Diffie-Hellman76,RSA78] Q:how to agree on key in sender,receiver do not first place(particularly if share secret key never“met")? public encryption key known to all private decryption key known only to receiver Security:8-16
Public Key Cryptography Security: 8- 16 symmetric key crypto: ▪ requires sender, receiver know shared secret key ▪Q: how to agree on key in first place (particularly if never “met”)? public key crypto ▪ radically different approach [Diffie-Hellman76, RSA78] ▪ sender, receiver do not share secret key ▪ public encryption key known to all ▪ private decryption key known only to receiver
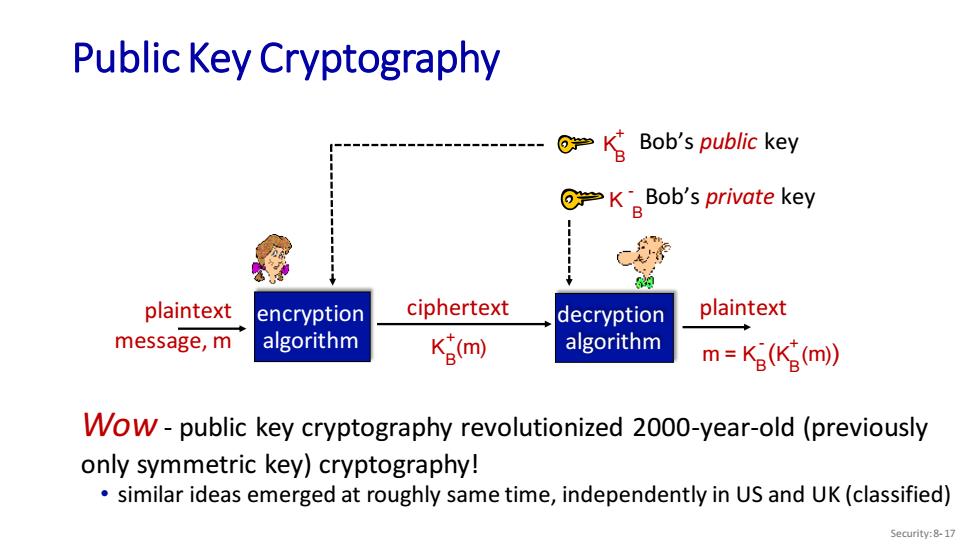
Public Key Cryptography ⑥=KBob's public key ⑥KBob's private key plaintext encryption ciphertext decryption plaintext message,m algorithm K含m algorithm m-Kg(Kg(m)) Wow-public key cryptography revolutionized 2000-year-old(previously only symmetric key)cryptography! similar ideas emerged at roughly same time,independently in US and UK(classified) Security:8-17
Public Key Cryptography Security: 8- 17 m = K (K (m)) B + B - plaintext encryption algorithm decryption K (m) algorithm B + plaintext ciphertext message, m K B + Bob’s public key K Bob’s private key B - Wow - public key cryptography revolutionized 2000-year-old (previously only symmetric key) cryptography! • similar ideas emerged at roughly same time, independently in US and UK (classified)

Public key encryption algorithms requirements: 1 need()andK()such that Ke(KB(m))m 2) given public key K,it should be impossibleto compute private key Kg RSA:Rivest,Shamir,Adelson algorithm Security:8-18
Public key encryption algorithms Security: 8- 18 requirements: RSA: Rivest, Shamir, Adelson algorithm 1 need K ( ) and K ( ) such that B B . . + - K (K (m)) = m B B - + given public key K , it should be impossible to compute private key K B B 2 + -

Prerequisite:modular arithmetic x mod n=remainder of x when divide by n ■facts: [(a mod n)+(b mod n)]mod n=(a+b)mod n [(a mod n)-(b mod n)]mod n =(a-b)mod n [(a mod n)*(b mod n)]mod n=(a*b)mod n ■thus (a mod n)d mod n=ad mod n example:x=14,n=10,d=2: (x mod n)d mod n=42 mod 10=6 xd=142=196xdm0d10=6 Security:8-19
Prerequisite: modular arithmetic Security: 8- 19 ▪ x mod n = remainder of x when divide by n ▪ facts: [(a mod n) + (b mod n)] mod n = (a+b) mod n [(a mod n) - (b mod n)] mod n = (a-b) mod n [(a mod n) * (b mod n)] mod n = (a*b) mod n ▪ thus (a mod n)d mod n = ad mod n ▪ example: x=14, n=10, d=2: (x mod n)d mod n = 42 mod 10 = 6 x d = 142 = 196 xd mod 10 = 6

RSA:getting ready message:just a bit pattern -bit pattern can be uniquely represented by an integer number thus,encrypting a message is equivalent to encrypting a number example: m=10010001.This message is uniquely represented by the decimal number 145. to encrypt m,we encrypt the corresponding number,which gives a new number (the ciphertext). Security:8-20
RSA: getting ready Security: 8- 20 ▪ message: just a bit pattern ▪ bit pattern can be uniquely represented by an integer number ▪ thus, encrypting a message is equivalent to encrypting a number example: ▪ m= 10010001. This message is uniquely represented by the decimal number 145. ▪ to encrypt m, we encrypt the corresponding number, which gives a new number (the ciphertext)