新疆大学：《工程力学》课程教学资源（PPT课件）第八章 弹性杆横截面上的正应力分析

横截面上正应力分析 1. 正应力分析的超静定性质 当外力已知时，可由平衡方程求得内力 分量静定问题。 口当内力分量已知时，只能确定应力与相 关内力分量之间的关系，却无法求得各 点应力一超静定问题

横截面上正应力分析 1. 正应力分析的超静定性质 当外力已知时，可由平衡方程求得内力 分量—静定问题。 当内力分量已知时，只能确定应力与相 关内力分量之间的关系，却无法求得各 点应力—超静定问题

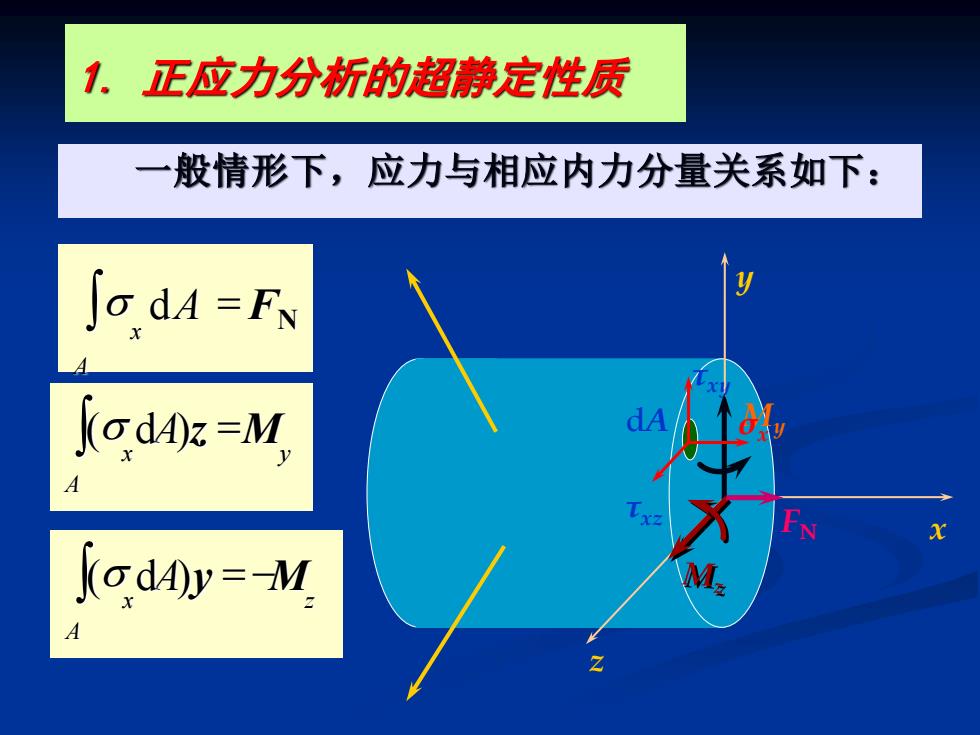
1.正应力分析的超静定性质 一般情形下，应力与相应内力分量关系如下： ∫odA=F Kod4)=M kodAy=M

一般情形下，应力与相应内力分量关系如下： 1. 正应力分析的超静定性质 x y z My FN  =− A x M z ( dA)y  = A x M y ( dA)z  = A x dA FN  σx τxy τxz dA

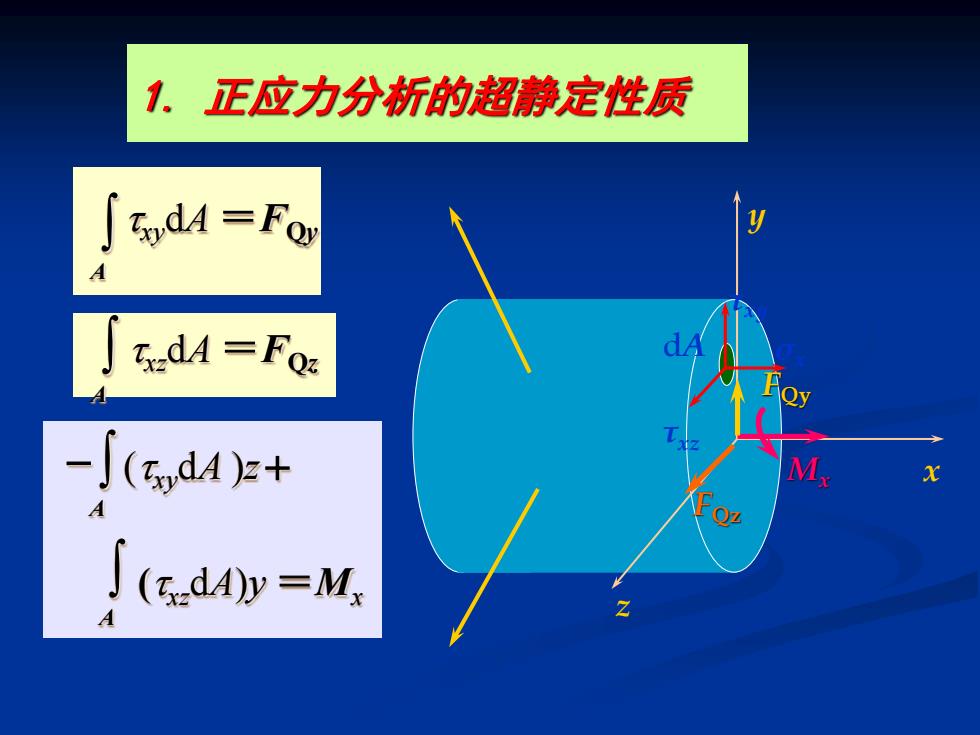
1.正应力分析的超静定性质 TodA=Foy tdA =Fo: -∫(，dAz+ A (dA)y=M

x y z Mx FQy FQz  A (xzdA)y ＝Mx −  + A (xydA )z  A xzdA ＝FQz  A xydA ＝FQy σx τxy τxz dA 1. 正应力分析的超静定性质

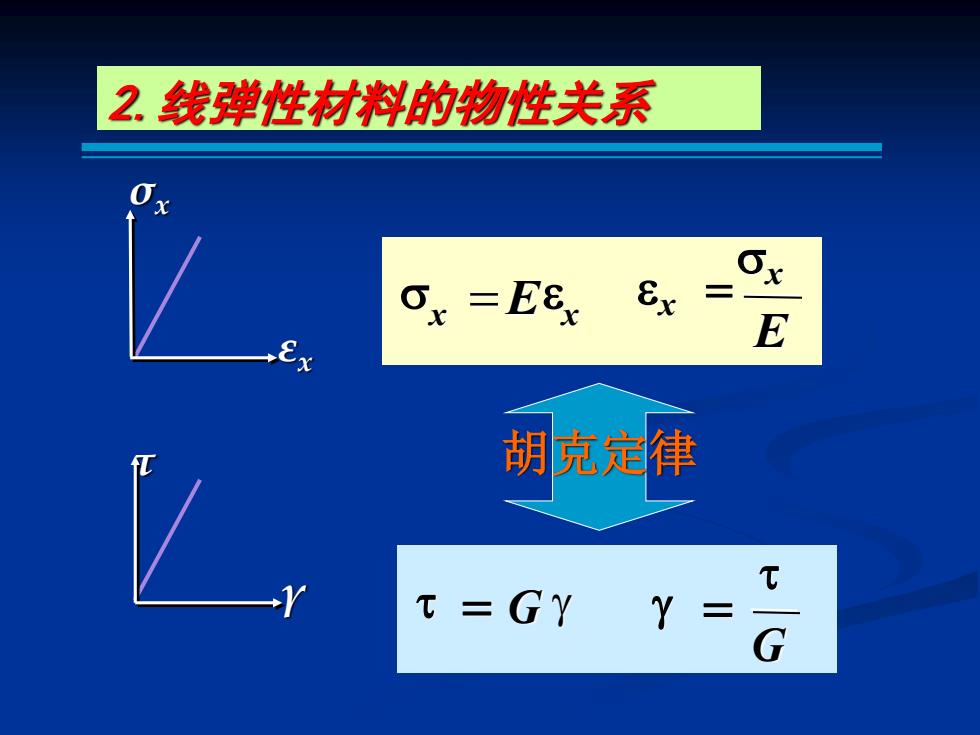
2.线弹性材料的物性关系 Ex 65 E 胡克定律 t t= GY Y= G

2.线弹性材料的物性关系   x =E x x x E =  = G g σx εx g  = G τ γ 胡克定律

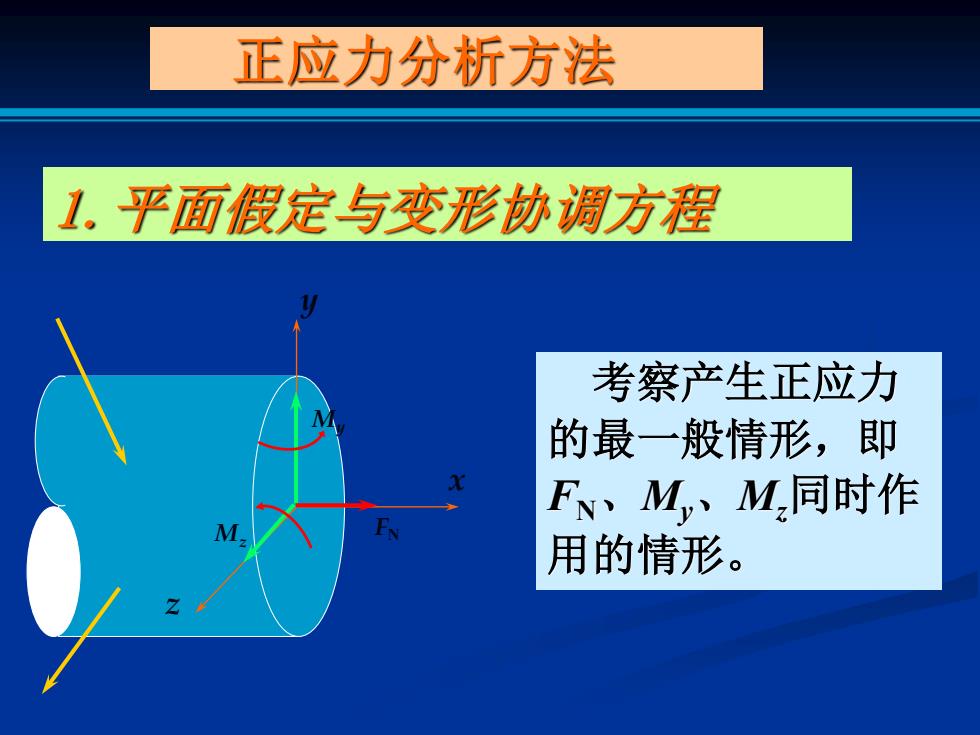
正应力分析方法 1。平面假定与变形协调方程 考察产生正应力 的最一般情形，即 FN、M、M,同时作 用的情形

1.平面假定与变形协调方程 考察产生正应力 的最一般情形，即 FN、My、Mz同时作 用的情形。 y x z My M FN z 正应力分析方法