
第一节简谐振动 第四章振动 常数A和P的确定 x=Acos(a+) Lv=-A@sin(ot+p) 初始条件t=0x=x,)=V0 2 A 0 00 tanΦ Wxo 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. 98898
第四章 振动 2 2 2 0 0 v A = x + 0 0 tan x − v = ◆ 常数 A 和 的确定 = 0 = 0 v = v0 初始条件 t x x x0 = Acos v0 = −Asin 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. v = −A sin(t +) x = Acos(t +) 第一节 简谐振动
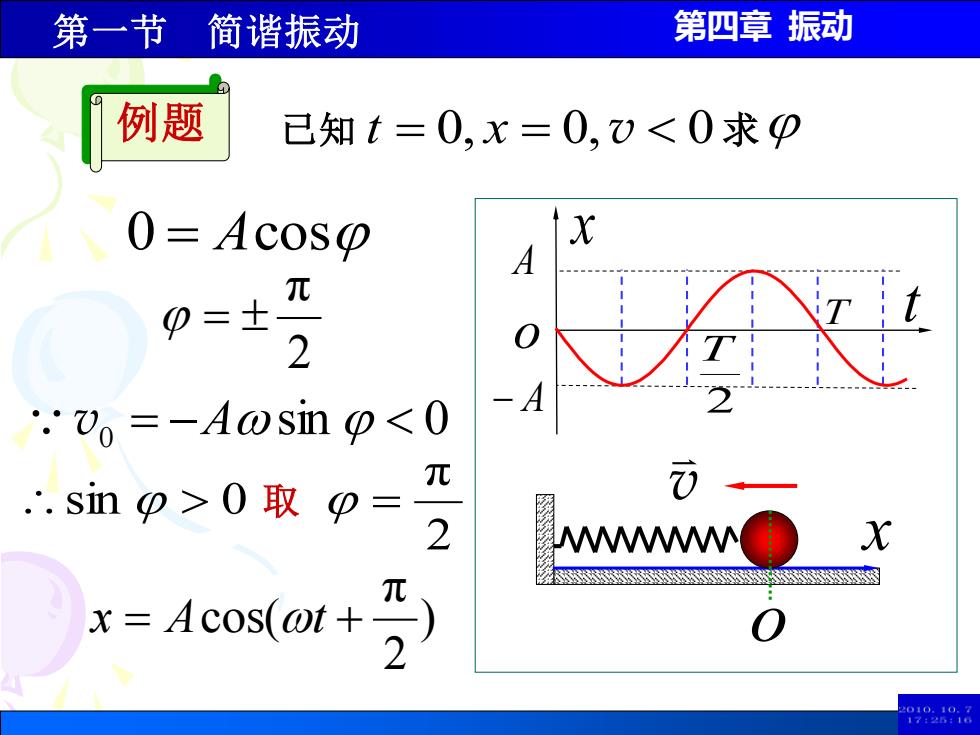
第一节简谐振动 第四章振动 例题 已知t=0,x=0,)<0求p 0=Acoso A 元 p=士 2 .vo=-A@sin <0 元 .sinp>0取p= 0 2 M X 猴图 x=Acos(@t+ 2 9898
第四章 振动 0 = Acos 2 π = v0 = −Asin 0 2 π sin 0 取 = 例题 已知 t = 0, x = 0, v 0 求 x v ) o 2 π x = Acos(t + A − A x T 2 T t o 第一节 简谐振动
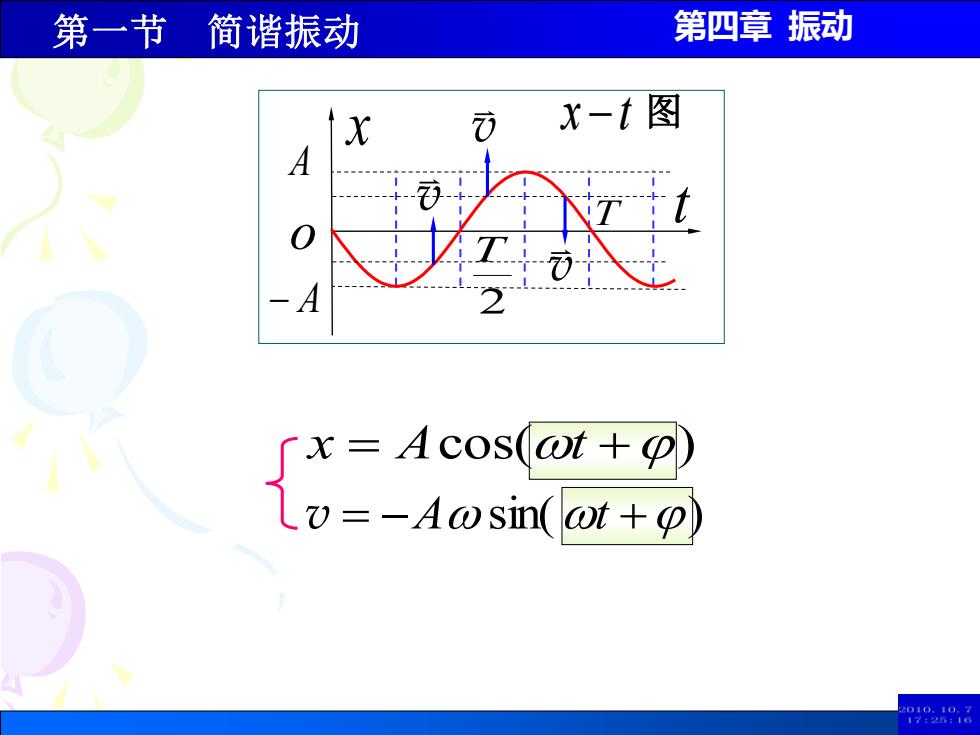
第一节 简谐振动 第四章振动 X x-t图 A 〔x=Acos(ot+p) Lv=-Aosin(ot+p) 2010.10:7 17:26:1
第四章 振动 x − t 图 A− A x T 2T t ov = −A sin(t +) x = Acos(t +) v v v 第一节 简谐振动

第一节简谐振动 第四章振动 4、相位差 两个同频率的简谐运动 x1=A,c0s(0t+p1) x2=A2C0s(0t+p2) △0=(ot+02)-(ot+p,) △0=02-91 0898
第四章 振动 4、相位差 cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t ( ) ( ) = + 2 − +1 t t = 2 −1 第一节 简谐振动 两个同频率的简谐运动
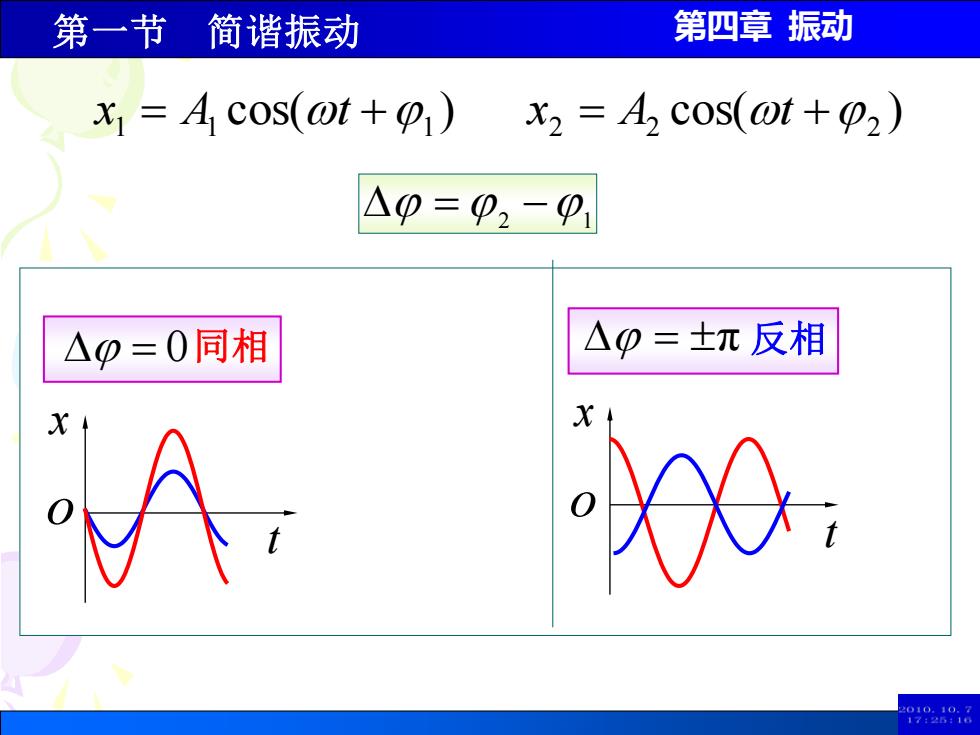
第一节简谐振动 第四章振动 x=A cos(ot+) x2 =A2 cos(@t+2) △0=p2-p1 △0=0同相 △0=士元反相 2010.10:7 17251
第四章 振动 = 0 x t o 同相 cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t = 2 −1 t x o = π 反相 第一节 简谐振动