
6.2.2分子性质 每个分子运动具有偶然性,然而正是由于每个分子的偶 然性,才使得大量分子运动出现了规律性。这种规律性具 有统计平均意义,称为统计规律性。 在平衡态,当重力的影响可以忽略时,容积内各处的压 强、密度、温度都相同,而分子始终在作无规则的热运动, 故我们可以认为: (①每个分子向各个方向运动的机会均等(。), (②)对于大量分子,向各个方向运动的分子数平均相等); 首页上页下页退出
首 页 上 页 下 页 退 出 11 6.2.2 分子性质 每个分子运动具有偶然性,然而正是由于每个分子的偶 然性,才使得大量分子运动出现了规律性。这种规律性具 有统计平均意义,称为统计规律性。 在平衡态,当重力的影响可以忽略时,容积内各处的压 强、密度、温度都相同,而分子始终在作无规则的热运动, 故我们可以认为: 6 1 (1) 每个分子向各个方向运动的机会均等( ); 6 N (2) 对于大量分子,向各个方向运动的分子数平均相等( );

(3)分子速度在各个方向上的分量的各种平均值平均相等; 例如:v2=v2+v2+ - (4)每个分子运动速度不尽相同,由于分子不停地发生碰 撞而发生变化,因而分子具有各种可能的速度。对于全同 分子,不会因碰撞而丢失具有某一速度的分子。 以上就是用统计平均的观点所得出的气体分子的性质。 12 首页上页下页退出
首 页 上 页 下 页 退 出 12 以上就是用统计平均的观点所得出的气体分子的性质。 (4) 每个分子运动速度不尽相同,由于分子不停地发生碰 撞而发生变化,因而分子具有各种可能的速度。对于全同 分子,不会因碰撞而丢失具有某一速度的分子。 2 2 2 2 3 1 v v v v x = y = z = 例如: 2 2 2 2 x y z v = v + v +v (3) 分子速度在各个方向上的分量的各种平均值平均相等;
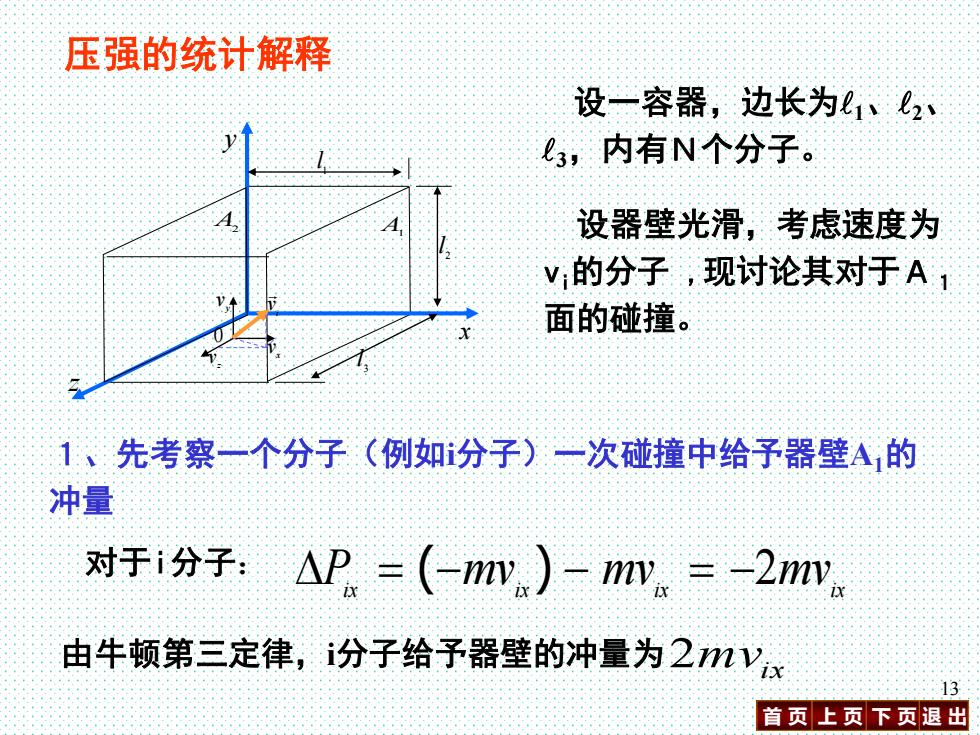
压强的统计解释 设一容器,边长为1、2、 3,内有N个分子。 设器壁光滑,考虑速度为 v的分子,现讨论其对于A1 面的碰撞。 1、先考察一个分子(例如分子)一次碰撞中给予器壁A的 冲量 对于i分子:△P=(-myn)-mw.=-2mv 由牛顿第三定律,分子给予器壁的冲量为2mVx 13 首页上页下页退出
首 页 上 页 下 页 退 出 13 压强的统计解释 设器壁光滑,考虑速度为 vi的分子 ,现讨论其对于A1 i 面的碰撞。 v x v y v z v x y z 1 l 2 l 3 l A1 A2 0 设一容器,边长为1、2、 3,内有N个分子。 Pix mvix mvix mvix 对于i分子: = (− ) − = −2 1、先考察一个分子(例如i分子)一次碰撞中给予器壁A1的 冲量 由牛顿第三定律, 2mvix i分子给予器壁的冲量为

2、分子在单位时间内施于A面的平均冲力 1分子单位时间内与A面碰撞的次数为 21, 则分子单位时间内施于A面的总冲量(冲力)为 2mvix =m心其量纲关系为(力秒 211 次秒 →力) 3、所有分子在单位时间内对器壁的冲力一对求和 ∑2=呢+吸++ 故若令 2=++.+呢 表示分子在X方向速率平 N 方的平均值, 14 首页上页下页退出
首 页 上 页 下 页 退 出 14 2、i分子在单位时间内施于A1面的平均冲力 i分子单位时间内与A1面碰撞的次数为 2 1 l vix 则 i分子单位时间内施于A1面的总冲量(冲力)为 2 1 2 l v mv ix ix 力) 秒 次 其量纲关系为(力 秒 → 3、所有分子在单位时间内对器壁的冲力──对i求和 2 1 1 1 ix N i A v l m F = = 2 2 2 2 1 1 2 x x Nx N i i x v = v + v + + v = N v v v v x x Nx x 2 2 2 2 2 1 + + + = 故若令 表示分子在X方向速率平 方的平均值, 2 1 1 mvix l = = = N i ix v l m 1 2 1

那么∑=N网 于是所有分子在单位时间内施于A面的冲力为 FaNM 4、求压强的统计平均值 由压强的定义 P= Fa 3 N 令ns 11,1 一为分子数密度(即单位体积内的分子数) 又由统计平均的观点有 所以 15 首页上页下页退出
首 页 上 页 下 页 退 出 15 2 1 2 x N i ix v = Nv = 那么 于是所有分子在单位时间内施于A1面的冲力为 2 1 x Nv l m = = = = = N i i x i x N i A v l m v l m F 1 2 1 2 1 1 1 4、求压强的统计平均值 1 2 3 l l l N 令 n = ──为分子数密度(即单位体积内的分子数) 又由统计平均的观点有 2 2 3 1 v v x = 所以 2 3 1 P = nmv 2 3 1 l l F P A 由压强的定义 = 2 1 2 3 x mv l l l N = ) 2 1 ( 3 2 2 = n mv