
处在相互热平衡状态的系统必定拥有某一个共同的物理性 质,我们把描述系统这一共同宏观性质的物理量称为系统的 温度。 2、温标温度计 温度计:即测温的工具。 温度计要能定量表示和测量温度,还需要建立温标一即 温度的数值表示法。 ※主要有三个步骤 其一、要选定一种合适物质(称测温质)的测温特性; 其二、规定测温质的测温特性与温度的依赖关系(线性); 其三、选定温度的标准点(固定点),并把一定间隔的冷 热程度分为若干度。 首页上页下页退出
首 页 上 页 下 页 退 出 6 处在相互热平衡状态的系统必定拥有某一个共同的物理性 质,我们把描述系统这一共同宏观性质的物理量称为系统的 温度 。 2、温标 温度计 温度计要能定量表示和测量温度,还需要建立温标 ──即 温度的数值表示法。 其一、要选定一种合适物质(称测温质)的测温特性; 其二、规定测温质的测温特性与温度的依赖关系(线性); 其三、选定温度的标准点(固定点),并把一定间隔的冷 热程度分为若干度。 ※ 主要有三个步骤 温度计:即测温的工具

※选用不同的测温物质或不同的测温特性,测量同一系统所 得的温度数值,一般情况下并不完全相同。 例如,(一个大气压下) 对水的冰点,华氏温标为32,攝氏温标为0C, 对水的沸点,华氏温标为212F,攝氏温标为100C。 3、热力学温标 一种与测温质和测温特性无关的温标。开尔文(lord Kelvin)在热力学第二定律的基础上建立了这种温标,称热 力学温标。 规定水的三相点(水,冰和水蒸汽平衡共存的状态)为 273.16K。 由热力学温标可导出摄氏温度 T=t+273.15 首页上页下页退出
首 页 上 页 下 页 退 出 7 3、热力学温标 规定水的三相点(水,冰和水蒸汽平衡共存的状态)为 273.16K。 一种与测温质和测温特性无关的温标。开尔文(lord Kelvin)在热力学第二定律的基础上建立了这种温标,称热 力学温标。 例如,(一个大气压下) 对水的冰点,华氏温标为32F0,攝氏温标为0C0 , 对水的沸点,华氏温标为212F0,攝氏温标为100C0 。 由热力学温标可导出摄氏温度 T=t+273.15 ※选用不同的测温物质或不同的测温特性,测量同一系统所 得的温度数值,一般情况下并不完全相同

6.1.3 理想气体状态方程 1、理想气体 从宏观定义:在室温下P不太大P不太高三大实验定律所得结罐想化 从微观定义忽略分子间作用分子间分子与器壁间碰撞视弹性碰撞 2、理想气体的状态方程 热平衡态下,系统各个状态参量之间满足一定的关系,这样 的关系叫系统的状态方程 过程方程 PY PV2 T M 克拉珀龙方程 P= RT Mmol 式中R是气体普适常量,在SI中R=8.31(J-mol-1.K), Mmo是气体的摩尔质量。 首页上页下页退出
首 页 上 页 下 页 退 出 8 6.1.3 理想气体状态方程 1、理想气体 2、理想气体的状态方程 热平衡态下,系统各个状态参量之间满足一定的关系,这样 的关系叫系统的状态方程 。 。 从微观定义:忽略分子间作用力,分子间,分子与器壁间碰撞视为弹性碰撞 从宏观定义:在室温下,ρ不太大,P不太高 ,三大实验定律所得结论理想化 克拉珀龙方程 RT M M PV mol = 式中R是气体普适常量,在SI中 R=8.31 (J·mol-1·K-1 ), Mmol是气体的摩尔质量。 过程方程 2 2 2 1 1 1 T PV T PV =
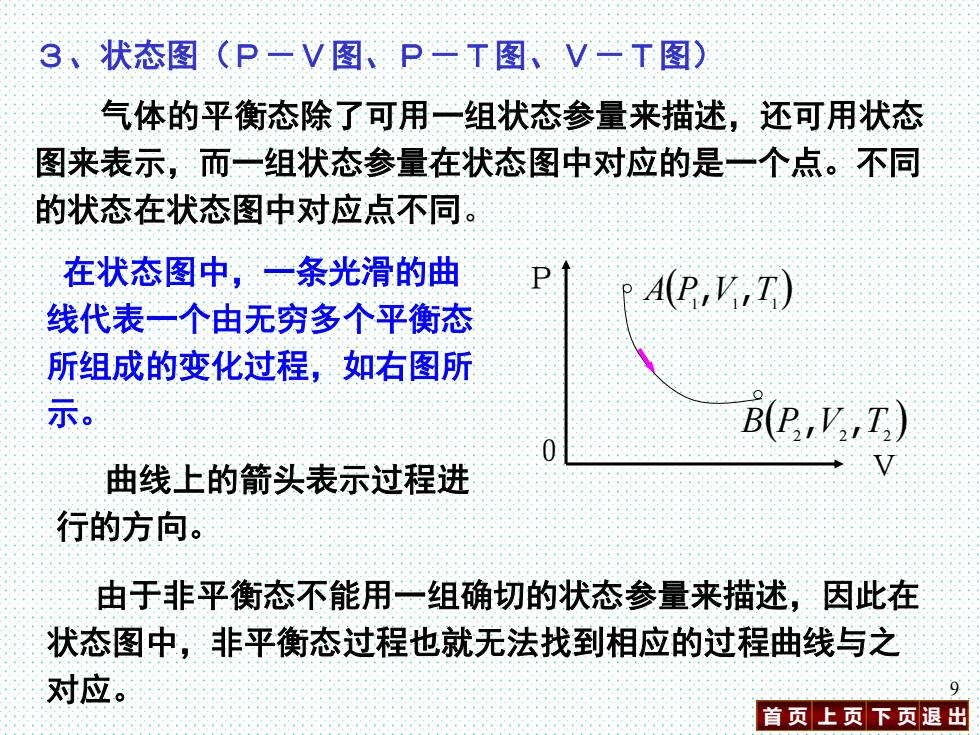
3、状态图(P一V图、P一T图、V一T图) 气体的平衡态除了可用一组状态参量来描述,还可用状态 图来表示,而一组状态参量在状态图中对应的是一个点。不同 的状态在状态图中对应点不同。 在状态图中,一条光滑的曲 P A(P,V,T) 线代表一个由无穷多个平衡态 所组成的变化过程,如右图所 示。 B(C,',I) 曲线上的箭头表示过程进 行的方向。 由于非平衡态不能用一组确切的状态参量来描述,因此在 状态图中,非平衡态过程也就无法找到相应的过程曲线与之 对应。 入 首页上页下页退出
首 页 上 页 下 页 退 出 9 3、状态图(P-V图、P-T图、V-T图) 气体的平衡态除了可用一组状态参量来描述,还可用状态 图来表示,而一组状态参量在状态图中对应的是一个点。不同 的状态在状态图中对应点不同。 在状态图中,一条光滑的曲 线代表一个由无穷多个平衡态 所组成的变化过程,如右图所 示。 ( ) A P1 V1 T1 , , ( ) B P2 V2 T2 , , P 曲线上的箭头表示过程进 0 V 行的方向。 由于非平衡态不能用一组确切的状态参量来描述,因此在 状态图中,非平衡态过程也就无法找到相应的过程曲线与之 对应

§6-2理想气体压强公式 6.2.1分子模型 1、分子可以看作质点。(除特别考虑) 2、除碰撞外,分子之间,分子与器壁不计相互作用力。 3、分子间,分子与器壁间的碰撞是完全弹性的,遵守 动量和能量守恒定律。 即:理想气体分子可看作彼此间无相互作用的遵守 经典力学规律的弹性质点。 10 首页上页下页退出
首 页 上 页 下 页 退 出 10 §6-2 理想气体压强公式 6.2.1 分子模型 3、分子间,分子与器壁间的碰撞是完全弹性的,遵守 动量和能量守恒定律。 即: 理想气体分子可看作彼此间无相互作用的遵守 经典力学规律的弹性质点。 1、分子可以看作质点。(除特别考虑) 2、除碰撞外,分子之间,分子与器壁不计相互作用力