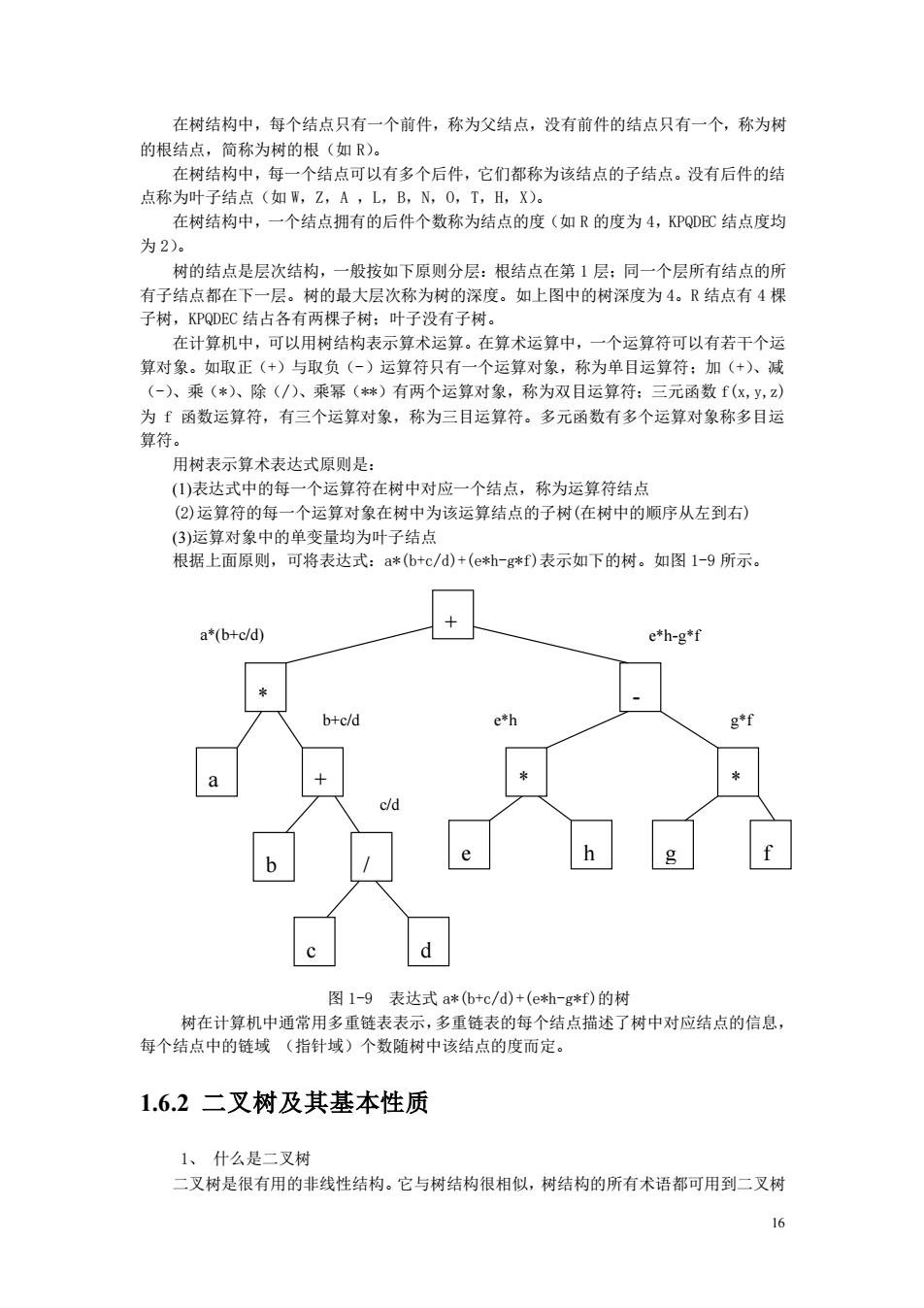
在树结构中,每个结点只有一个前件,称为父结点,没有前件的结点只有一个,称为树 一个结点可以有多个后件,它们都称为该结点的子结点。没有后件的结 点称为叶子结点(如W,Z,A,L,B,N,0,T,H,X)。 在树结构中,一个结点拥有的后件个数称为结点的度(如R的度为4,KPQDEC结点度均 为2)。 树的结点是层次结构,一般按如下原则分层:根结点在第1层:同一个层所有结点的所 有子结点都在下 一层。树的最大层次称为树的深度。如上图中的树深度为4。R结点有4棵 子树,KPQDEC结占各有两棵子树:叶子没有子树。 在计算机中,可以用树结构表示算术运算。在算术运算中,一个运算符可以有若干个运 算对象。如取正(+)与取负()运算符只有一个运算对象,称为单目运算符:加(+人减 (-)、乘(*)、除(/)、乘察(球)有两个运算对象,称为双目云算符:三元函数f(x,V,z) ,称为三目运算符。多元函数有多个运算对象称多目运 用树表示算术表达式原则是: ()表达式中的每一个运算符在树中对应一个结点,称为运算符结点 (2)运算符的每一个运算对象在树中为该运算结点的子树(在树中的顺序从左到右) 3运算对象中的单变量均为叶子结占 根据上面原则, 可将表达式:a*(+c/d)+(eh-g*f)表示如下的树。如图1-9所示 a*(b+c/d) + e*h-g*f b+c/d c d 图1-9表达式a*(b+c/d)+(e补-g*f)的树 树在计算机中通常用多重链表表示,多重链表的每个结点描述了树中对应结点的信息, 每个结点中的链域(指针域)个数随树中该结点的度而定。 1.6.2二叉树及其基本性质 1小、什么是二叉树 二叉树是很有用的非线性结构。它与树结构很相似,树结构的所有术语都可用到二叉树 6
16 在树结构中,每个结点只有一个前件,称为父结点,没有前件的结点只有一个,称为树 的根结点,简称为树的根(如 R)。 在树结构中,每一个结点可以有多个后件,它们都称为该结点的子结点。没有后件的结 点称为叶子结点(如 W,Z,A ,L,B,N,O,T,H,X)。 在树结构中,一个结点拥有的后件个数称为结点的度(如 R 的度为 4,KPQDEC 结点度均 为 2)。 树的结点是层次结构,一般按如下原则分层:根结点在第 1 层;同一个层所有结点的所 有子结点都在下一层。树的最大层次称为树的深度。如上图中的树深度为 4。R 结点有 4 棵 子树,KPQDEC 结占各有两棵子树;叶子没有子树。 在计算机中,可以用树结构表示算术运算。在算术运算中,一个运算符可以有若干个运 算对象。如取正(+)与取负(-)运算符只有一个运算对象,称为单目运算符;加(+)、减 (-)、乘(*)、除(/)、乘幂(**)有两个运算对象,称为双目运算符;三元函数 f(x,y,z) 为 f 函数运算符,有三个运算对象,称为三目运算符。多元函数有多个运算对象称多目运 算符。 用树表示算术表达式原则是: (1)表达式中的每一个运算符在树中对应一个结点,称为运算符结点 (2)运算符的每一个运算对象在树中为该运算结点的子树(在树中的顺序从左到右) (3)运算对象中的单变量均为叶子结点 根据上面原则,可将表达式:a*(b+c/d)+(e*h-g*f)表示如下的树。如图 1-9 所示。 图 1-9 表达式 a*(b+c/d)+(e*h-g*f)的树 树在计算机中通常用多重链表表示,多重链表的每个结点描述了树中对应结点的信息, 每个结点中的链域 (指针域)个数随树中该结点的度而定。 1.6.2 二叉树及其基本性质 1、 什么是二叉树 二叉树是很有用的非线性结构。它与树结构很相似,树结构的所有术语都可用到二叉树 + * - a + b / c d * * e h g f a*(b+c/d) * b+c/d * c/d * e*h * e*h-g*f * g*f *
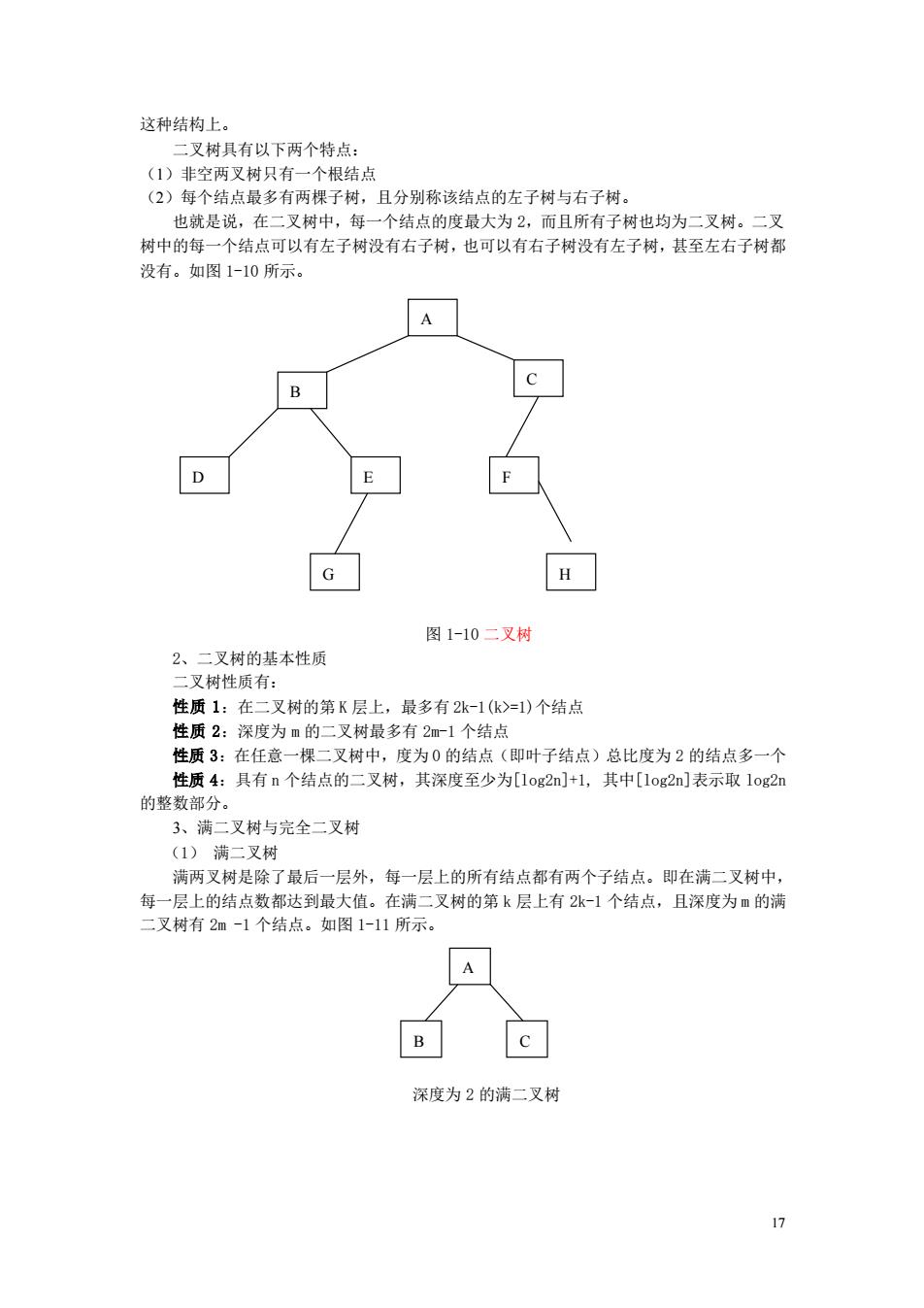
这种结构上。 二叉树其有以下两个特点: 两叉树只有 个根结 (2)每个结点最多有两棵子树,且分别称该结点的左子树与右子树。 也就是说,在二叉树中,每一个结点的度最大为2,而且所有子树也均为二叉树。二叉 树中的每一个结点可以有左子树没有右子树,也可以有右子树没有左子树,甚至左右子树都 没有。如图1-10所示。 A B D E G H 图1-10二叉树 2、二叉树的基本性质 二叉树性质有: 性质1:在二叉树的第K层上,最多有2k-1(k>-1)个结点 性质2:深度为m的二叉树最多有21个结点 性质3:在任意一棵二叉树中,度为0的结点(即叶子结点)总比度为2的结点多一个 性质4:具有n个结点的二叉树,其深度至少为[1og2n]+1,其中[1og2n]表示取1og2m 的整数部分。 3、满二叉树与完全二叉树 (1)满二义树 满两叉树是除了最后一层外,每一层上的所有结点都有两个子结点。即在满二叉树中, 每一层上的结点数都达到最大值。在满二叉树的第k层上有张-1个结点,且深度为m的满 二叉树有2m-1个结点。如图1-11所示。 A B c 深度为2的满二叉树
17 这种结构上。 二叉树具有以下两个特点: (1)非空两叉树只有一个根结点 (2)每个结点最多有两棵子树,且分别称该结点的左子树与右子树。 也就是说,在二叉树中,每一个结点的度最大为 2,而且所有子树也均为二叉树。二叉 树中的每一个结点可以有左子树没有右子树,也可以有右子树没有左子树,甚至左右子树都 没有。如图 1-10 所示。 图 1-10 二叉树 2、二叉树的基本性质 二叉树性质有: 性质 1:在二叉树的第 K 层上,最多有 2k-1(k>=1)个结点 性质 2:深度为 m 的二叉树最多有 2m-1 个结点 性质 3:在任意一棵二叉树中,度为 0 的结点(即叶子结点)总比度为 2 的结点多一个 性质 4:具有 n 个结点的二叉树,其深度至少为[log2n]+1, 其中[log2n]表示取 log2n 的整数部分。 3、满二叉树与完全二叉树 (1) 满二叉树 满两叉树是除了最后一层外,每一层上的所有结点都有两个子结点。即在满二叉树中, 每一层上的结点数都达到最大值。在满二叉树的第 k 层上有 2k-1 个结点,且深度为 m 的满 二叉树有 2m -1 个结点。如图 1-11 所示。 深度为 2 的满二叉树 A B C A B C D E F G H
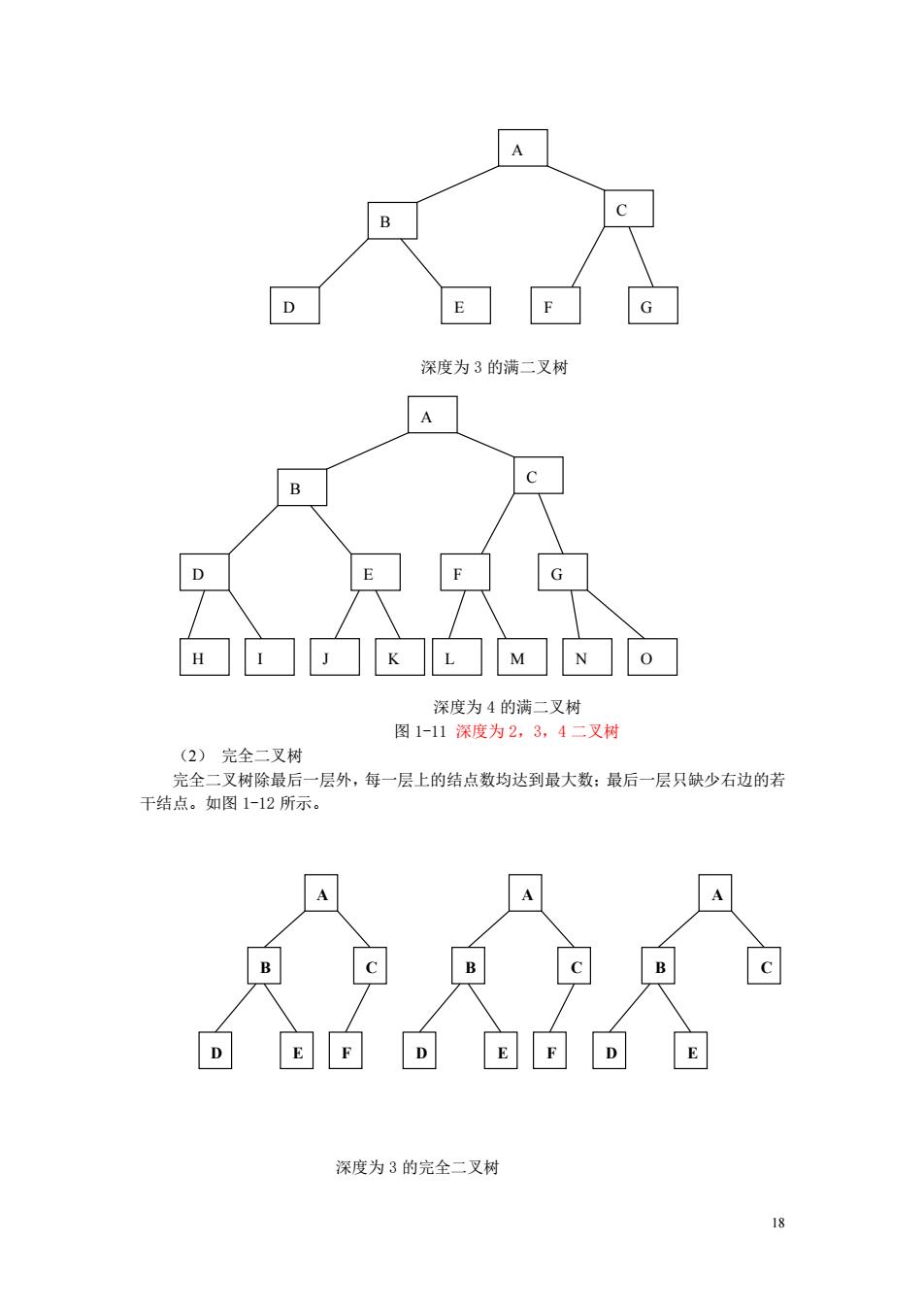
A E G 深度为3的满二叉树 A B D G 深度为4的满二叉树 图1-11深度为2,3,4二叉树 (2)完全二叉树 完全二叉树除最后一层外,每一层上的结点数均达到最大数:最后一层只缺少右边的若 干结点。如图1-12所示 c D 深度为3的完全二叉树
18 深度为 3 的满二叉树 深度为 4 的满二叉树 图 1-11 深度为 2,3,4 二叉树 (2) 完全二叉树 完全二叉树除最后一层外,每一层上的结点数均达到最大数;最后一层只缺少右边的若 干结点。如图 1-12 所示。 深度为 3 的完全二叉树 A F C D E B A F C D E B A C D E B A B C D E F G H I J K L M N O A B C D E F G
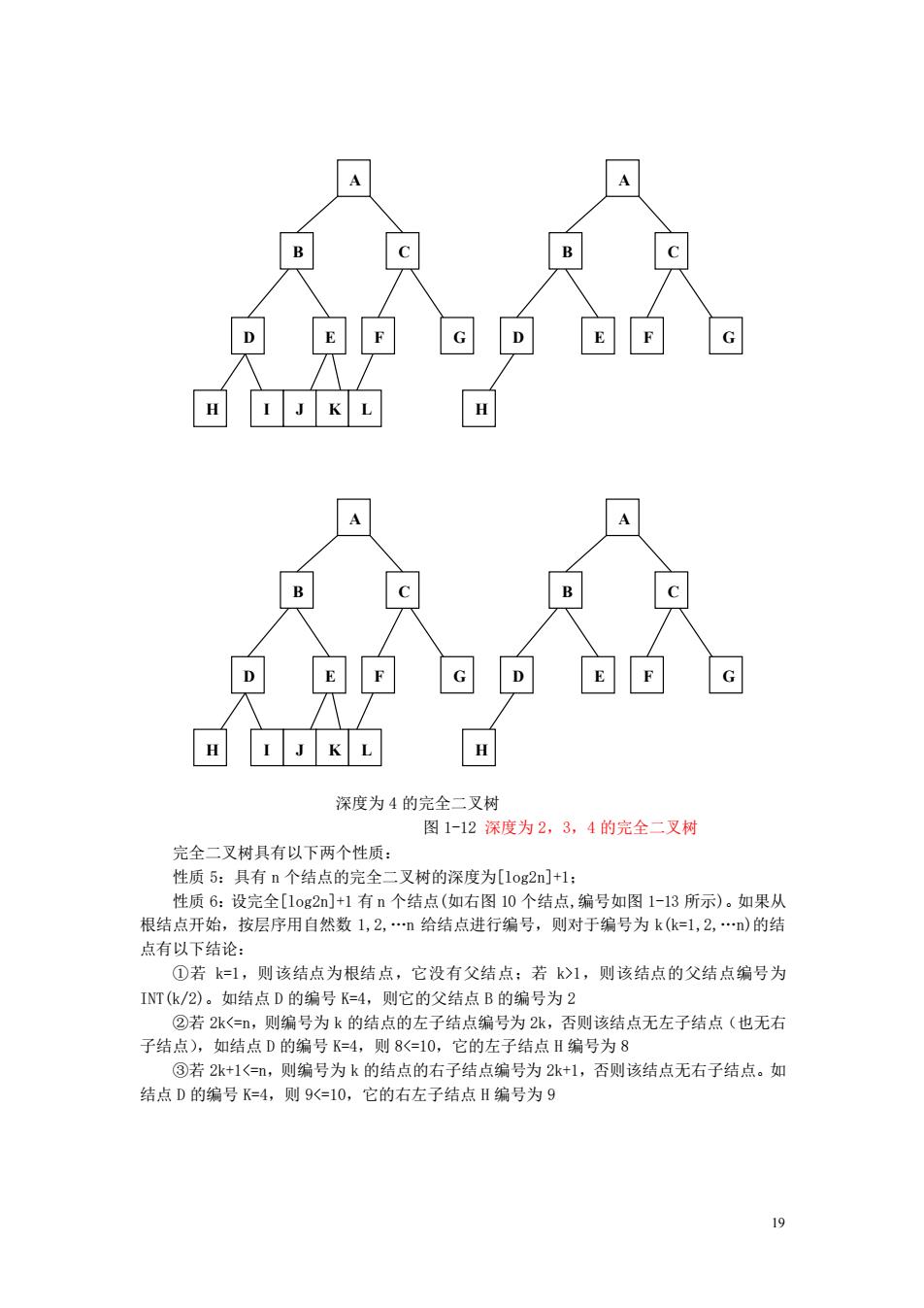
A B 包 B 1 J K L H A A B 中可 1 B1 J KL 深度为4的完全二叉树 图1-12深度为2,3,4的完全二叉树 完全二叉树具有以下两个性质: 性质5:具有n个结点的完全二叉树的深度为[1og2]+1: 性质6:设完全[1og2]+1有n个结点(如右图10个结点,编号如图1-13所示)。如果从 根结点开始,按层序用自然数1,2,n给结点进行编号,则对于编号为k(k=1,2,)的结 点有以下结论 ①若k=1,则该结点为根结点,它没有父结点:若k>1,则该结点的父结点编号为 INT(k/2)。如结点D的编号K=4,则它的父结点B的编号为2 ②若2k<=,则编号为k的结点的左子结点编号为2k,否则该结点无左子结点(也无右 子结点),如结点D的编号K=4,则8<=10,它的左子结点H编号为8 ③若2+1<,则编号为k的结点的右子结点编号为2张+1,否则该结点无右子结点。如 结点D的编号K=4,则9=10,它的右左子结点H编号为9
19 深度为 4 的完全二叉树 图 1-12 深度为 2,3,4 的完全二叉树 完全二叉树具有以下两个性质: 性质 5:具有 n 个结点的完全二叉树的深度为[log2n]+1; 性质 6:设完全[log2n]+1 有 n 个结点(如右图 10 个结点,编号如图 1-13 所示)。如果从 根结点开始,按层序用自然数 1,2,.n 给结点进行编号,则对于编号为 k(k=1,2,.n)的结 点有以下结论: ①若 k=1,则该结点为根结点,它没有父结点;若 k>1,则该结点的父结点编号为 INT(k/2)。如结点 D 的编号 K=4,则它的父结点 B 的编号为 2 ②若 2k<=n,则编号为 k 的结点的左子结点编号为 2k,否则该结点无左子结点(也无右 子结点),如结点 D 的编号 K=4,则 8<=10,它的左子结点 H 编号为 8 ③若 2k+1<=n,则编号为 k 的结点的右子结点编号为 2k+1,否则该结点无右子结点。如 结点 D 的编号 K=4,则 9<=10,它的右左子结点 H 编号为 9 A F C D E B G H I J K L A F C D E B G H A F C D E B G H I J K L A F C D E B G H
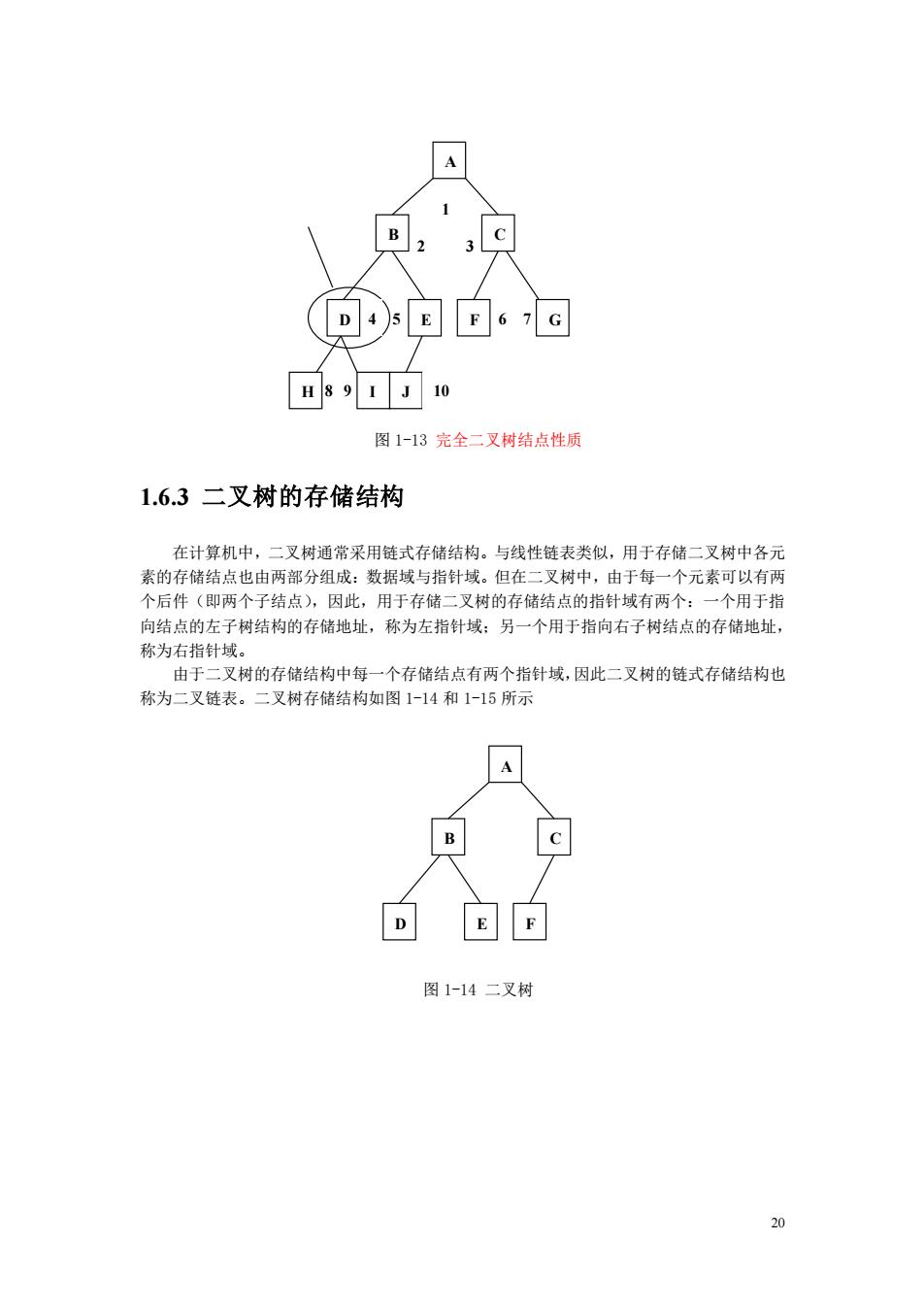
A (可4包回6© H891J10 图1-13完全二叉树结点性质 1.6.3二叉树的存储结构 在计算机中,二叉树通常采用链式存储结构。与线性链表类似,用于存储二叉树中各元 素的存储结点也由两部分组成:数据域与指针域。但在二叉树中,由于每一个元素可以有两 个后件(即两个子结点),因此,用于存储二叉树的存储结点的指针域有两个:一个用于指 向结点的左子树结构的存储地址,称为左指针域:另一个用于指向右子树结点的存储地址 称为右指针域 由于二叉树的存储结构中每一个存储结点有两个指针域,因此二叉树的链式存储结构也 称为二叉链表。二叉树存储结构如图1-14和1-15所示 D包E 图1-14二叉树
20 图 1-13 完全二叉树结点性质 1.6.3 二叉树的存储结构 在计算机中,二叉树通常采用链式存储结构。与线性链表类似,用于存储二叉树中各元 素的存储结点也由两部分组成:数据域与指针域。但在二叉树中,由于每一个元素可以有两 个后件(即两个子结点),因此,用于存储二叉树的存储结点的指针域有两个:一个用于指 向结点的左子树结构的存储地址,称为左指针域;另一个用于指向右子树结点的存储地址, 称为右指针域。 由于二叉树的存储结构中每一个存储结点有两个指针域,因此二叉树的链式存储结构也 称为二叉链表。二叉树存储结构如图 1-14 和 1-15 所示 图 1-14 二叉树 A F C D E B 5 2 9 7 1 4 6 A F C D E B G I J 1 3 H 8 10