
同时观察谱峰和零点的位置及他们与R,的关系。 问题3.2对一个可用带宽为10KHz的基带通信信道而言,A.1中每一个码型的最 大码元速率为多少? B.信道特性 在这一部分你将模拟一个通信信道的特点。代表信道响应的MATLAB函数是channel. 形式如下(提示:我们可以键入help channel来获取channel函数的帮助): channel(输入,增益,噪声功率,带宽) 噪声 信道 输出 (增益)》 输入 图3.1信道模型 B.1创建一个有10个抽样值的二进制序列b且用双极性不归零信号格式产生代表b的波形 其中R=1kbps。 >b=binary(10). >>x=wave gen(b,'polar nrz',1000). 根据A部分的数据,确定x的传输带宽B: B.= Hz B.2考虑一个具有归一化增益和加性白高斯噪声(AWGN的基带数字传输信道(噪声功率为 102w信道带宽为4.9KHZ),在此信道上传输波形x并显示输入和输出波形: >y=channel(x1,0.01,4900)方 >>subplot(211),waveplot(x). >>subplot(212).waveplot(y): 根据显示的输出波形估计b: b- ],把你的估计和原序列b比较 B.3信道噪声对传输波形的影响。逐渐地增加信道噪声功率,并保持信道带宽不变,我们可 以观察信道输出的变化: >>subplot(212),waveplot(channel(x,1,sigma,4900)); gma取0.1,0.51,2,5等值。在噪声功率为多少时,我们传输的信号将淹没在噪声之中 B.4你也可以通过看信道输出的功率谱密度来观察增加信道噪声功率的影响: >>b=binary(1000); >>x=wave gen(b,polar nrz,1000) >>clf.subplot(121).psd(x).a=axis. >>subplot(122),psd(channel(x,1,0.01,4900)); >>axis(a)hold on -17
―17― 同时观察谱峰和零点的位置及他们与 Rb的关系。 问题 3.2 对一个可用带宽为 10KHz 的基带通信信道而言,A.1 中每一个码型的最 大码元速率为多少? B.信道特性 在这一部分你将模拟一个通信信道的特点。代表信道响应的 MATLAB 函数是 channel, 形式如下(提示:我们可以键入 help channel 来获取 channel 函数的帮助): channel(输入,增益,噪声功率,带宽) B.1 创建一个有 10 个抽样值的二进制序列 b 且用双极性不归零信号格式产生代表 b 的波形, 其中 Rb=1kbps。 >> b = binary(10); >> x = wave_gen(b,’polar_nrz’,1000); 根据 A 部分的数据,确定 x 的传输带宽 BT: BT = Hz B.2 考虑一个具有归一化增益和加性白高斯噪声(AWGN)的基带数字传输信道(噪声功率为 10-2w,信道带宽为 4.9KHZ),在此信道上传输波形 x,并显示输入和输出波形: >> y = channel( x,1,0.01,4900 ); >> subplot(211),waveplot(x); >> subplot(212),waveplot(y); 根据显示的输出波形估计 b: b ^ =[ ],把你的估计和原序列 b 比较。 B.3 信道噪声对传输波形的影响。逐渐地增加信道噪声功率,并保持信道带宽不变,我们可 以观察信道输出的变化: >> subplot(212),waveplot( channel(x,1,sigma,4900)); sigma 取 0.1,0.5,1,2,5 等值。在噪声功率为多少时,我们传输的信号将淹没在噪声之中? B.4 你也可以通过看信道输出的功率谱密度来观察增加信道噪声功率的影响: >> b = binary(1000); >> x = wave_gen(b,‘polar_nrz’,1000); >> clf,subplot(121),psd(x),a = axis; >> subplot(122),psd(channel(x,1,0.01,4900)); >> axis(a),hold on 信道 (增益) 输入 输出 噪声 图 3.1 信道模型
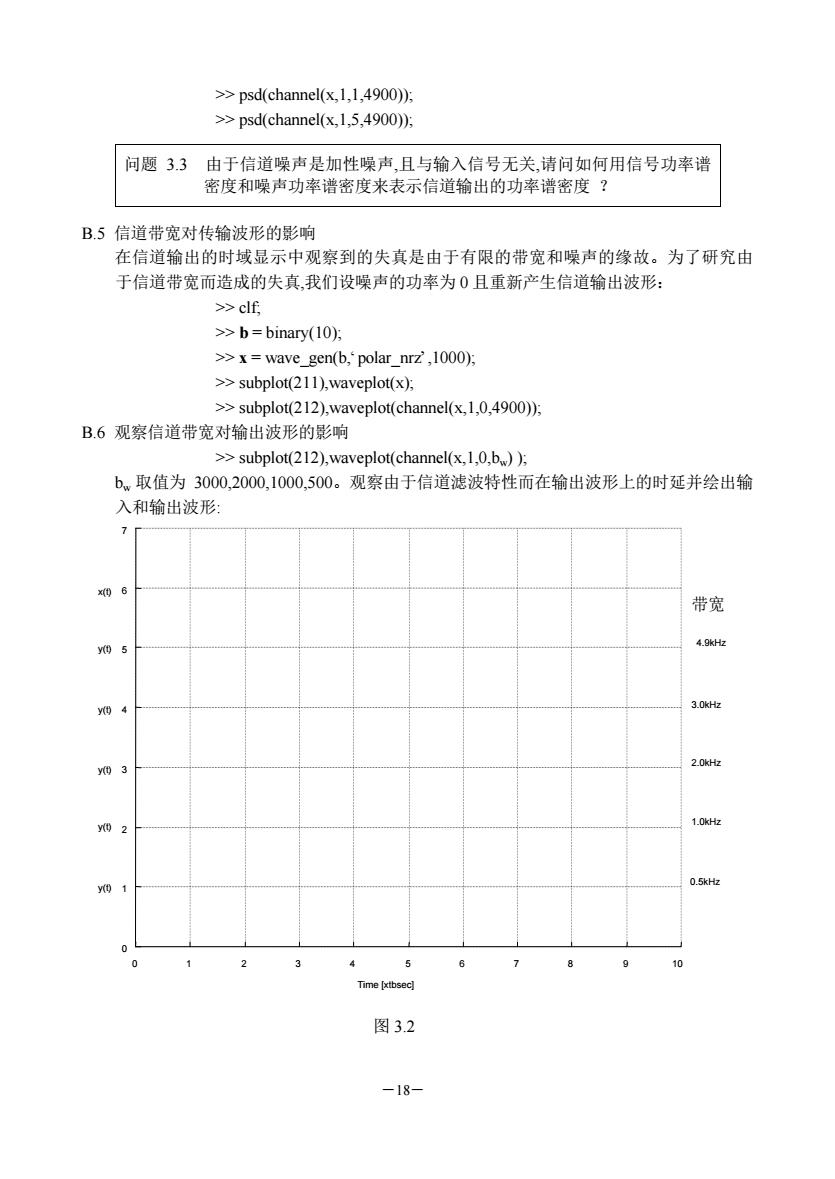
>>psd(channel(x,1,1,4900)): >>psd(channel(x,1,5,4900)): 问题3.3由于信道噪声是加性噪声,且与输入信号无关,请问如何用信号功率谱 密度和噪声功率谱密度来表示信道输出的功率谱密度? B.5信道带宽对传输波形的影响 在信道输出的时域显示中观察到的失真是由于有限的带宽和噪声的缘故。为了研究由 于信道带宽而造成的失真,我们设噪声的功率为0且重新产生信道输出波形: >>clf >>b=binary(10), >>x=wave _gen(b,'polar_nrz',1000); >>subplot(211),waveplot(x). >>subplot(212),waveplot(channel(x,1,0,4900)); B.6观察信道带宽对输出波形的影响 >>subplot(212),waveplot(channel(x.1.0.b.)): b.取值为3000,2000,1000,500。观察由于信道滤波特性而在输出波形上的时延并绘出输 入和输出波形 7 带宽 49 20H 0.5H me bo 图3.2 -18
―18― >> psd(channel(x,1,1,4900)); >> psd(channel(x,1,5,4900)); 问题 3.3 由于信道噪声是加性噪声,且与输入信号无关,请问如何用信号功率谱 密度和噪声功率谱密度来表示信道输出的功率谱密度 ? B.5 信道带宽对传输波形的影响 在信道输出的时域显示中观察到的失真是由于有限的带宽和噪声的缘故。为了研究由 于信道带宽而造成的失真,我们设噪声的功率为 0 且重新产生信道输出波形: >> clf; >> b = binary(10); >> x = wave_gen(b,‘polar_nrz’,1000); >> subplot(211),waveplot(x); >> subplot(212),waveplot(channel(x,1,0,4900)); B.6 观察信道带宽对输出波形的影响 >> subplot(212),waveplot(channel(x,1,0,bw) ); bw 取值为 3000,2000,1000,500。观察由于信道滤波特性而在输出波形上的时延并绘出输 入和输出波形: 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 Time [xtbsec] x(t) y(t) y(t) y(t) y(t) y(t) 带宽 4.9kHz 3.0kHz 2.0kHz 1.0kHz 0.5kHz 图 3.2
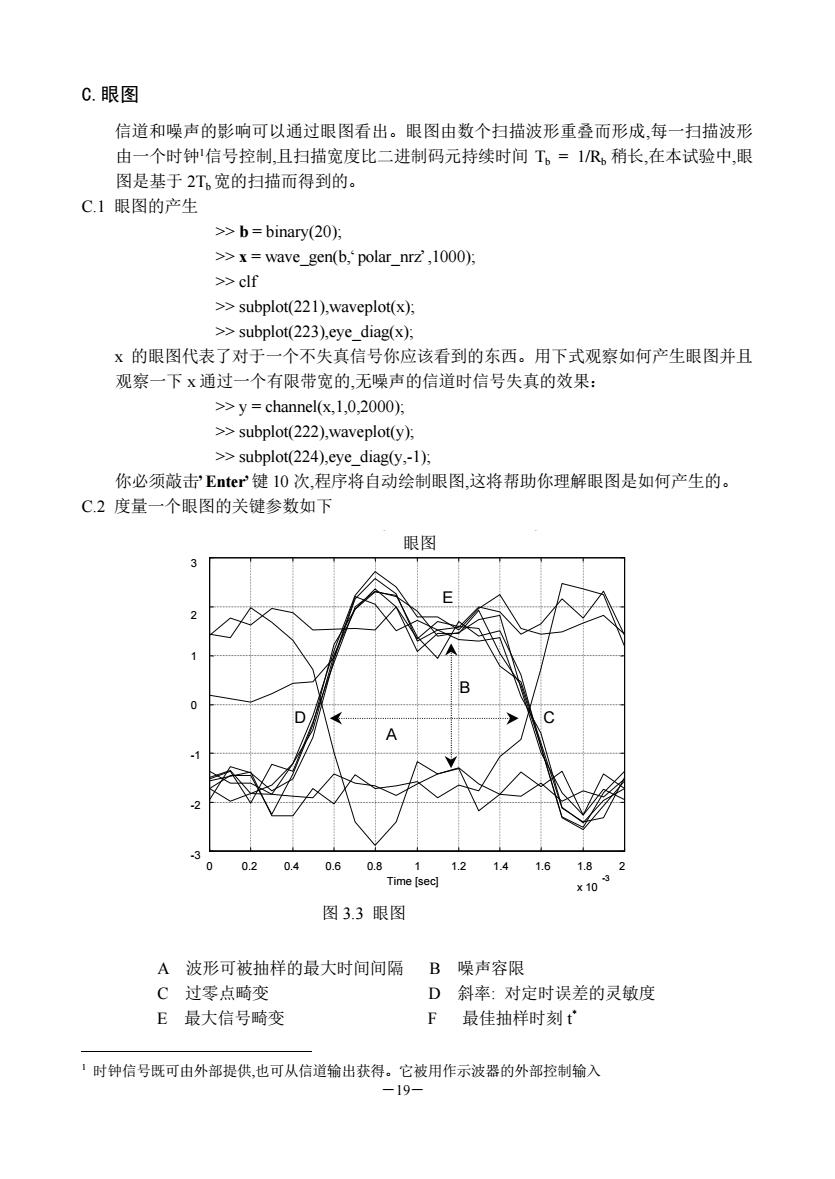
C.眼图 信道和噪声的影响可以通过眼图看出。眼图由数个扫描波形重叠而形成,每一扫描波形 由一个时钟信号控制,且扫描宽度比二进制码元持续时间T。=1/R稍长,在本试验中,眼 图是基于2T,宽的扫描而得到的。 C1眼图的产生 >>b=binary(20); >>x=wave_gen(b,'polar_nrZ,1000). >clf >subplot(221),waveplot(x). >>subplot(223),eye_diag(x); x的眼图代表了对于一个不失真信号你应该看到的东西。用下式观察如何产生眼图并且 观察一下x通过一个有限带宽的,无噪声的信道时信号失真的效果: >>y=channel(x,1,0.2000); >>subplot(222),waveplot(y); >>subplot(224).eye_diag(y,-1) 你必须敲击'Eter键10次,程序将自动绘制眼图,这将帮助你理解眼图是如何产生的。 C2度量一个眼图的关键参数如下 眼图 3 02 040.6 0.8 12 14 16 18 Time [sec] 图3.3眼图 A波形可被抽样的最大时间间隔B噪声容限 C时零点瞌变 D斜率:对定时误差的灵敏度 E最大信号畸变 F最佳抽样时刻 时钟信号既可由外部提供,也可从信道输出获得。它被用作示波器的外部控制输入
―19― C.眼图 信道和噪声的影响可以通过眼图看出。眼图由数个扫描波形重叠而形成,每一扫描波形 由一个时钟1信号控制,且扫描宽度比二进制码元持续时间 Tb = 1/Rb 稍长,在本试验中,眼 图是基于 2Tb 宽的扫描而得到的。 C.1 眼图的产生 >> b = binary(20); >> x = wave_gen(b,‘polar_nrz’,1000); >> clf >> subplot(221),waveplot(x); >> subplot(223),eye_diag(x); x 的眼图代表了对于一个不失真信号你应该看到的东西。用下式观察如何产生眼图并且 观察一下 x 通过一个有限带宽的,无噪声的信道时信号失真的效果: >> y = channel(x,1,0,2000); >> subplot(222),waveplot(y); >> subplot(224),eye_diag(y,-1); 你必须敲击’Enter’键 10 次,程序将自动绘制眼图,这将帮助你理解眼图是如何产生的。 C.2 度量一个眼图的关键参数如下 A 波形可被抽样的最大时间间隔 B 噪声容限 C 过零点畸变 D 斜率: 对定时误差的灵敏度 E 最大信号畸变 F 最佳抽样时刻 t * 1 时钟信号既可由外部提供,也可从信道输出获得。它被用作示波器的外部控制输入 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 x 10 -3 -3 -2 -1 0 1 2 3 Time [sec] 眼图 E B A D C 图 3.3 眼图
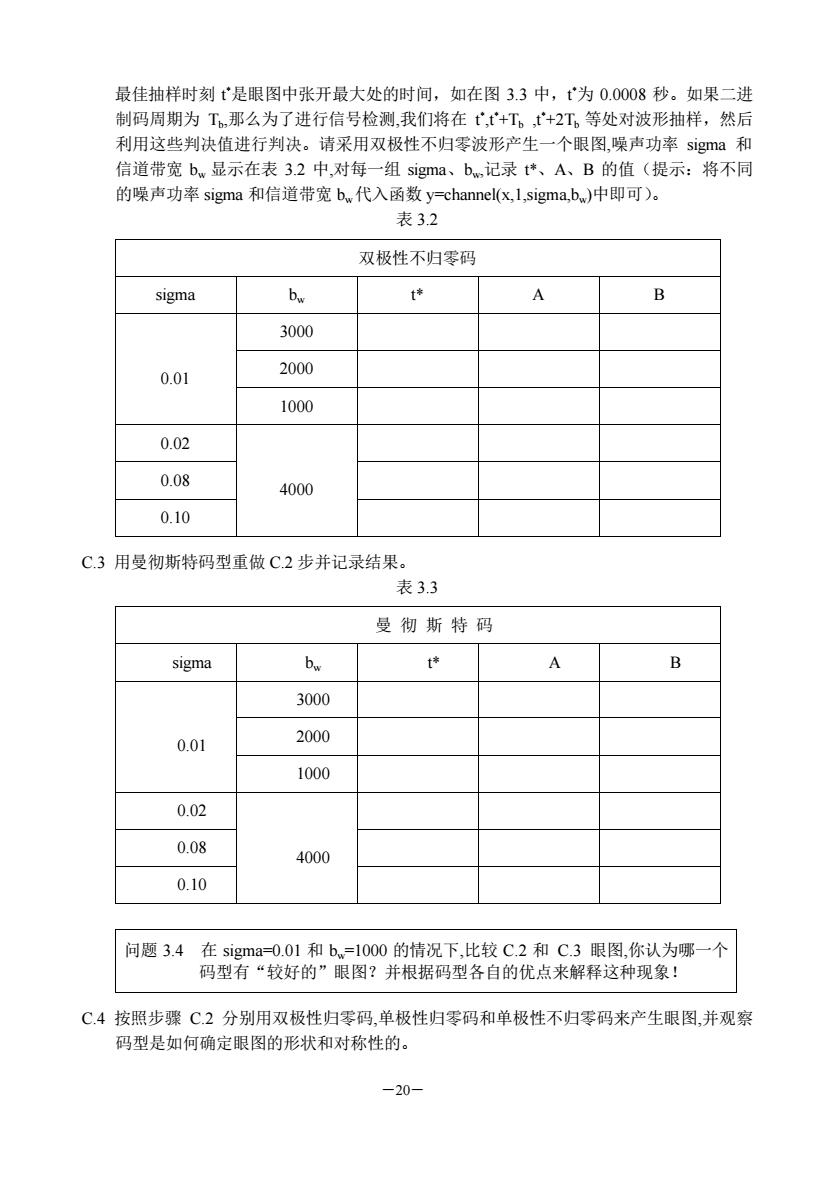
最佳抽样时刻是眼图中张开最大处的时间,如在图3.3中,为0.0008秒。如果二进 制码周期为T。那么为了进行信号检测我们将在t,t+T。+2工。等处对波形抽样,然后 利用这些判决值进行判决。请采用双极性不归零波形产生一个眼图,噪声功率siga和 信道带宽b.显示在表3.2中,对每一组sigma、b,记录t*、A、B的值(提示:将不同 的噪声功率sigma和信道带宽b代入函数y-channel(x.1,.sigma.b).中即可)。 表3.2 双极性不归零码 sigma be t B 3000 0.01 2000 1000 0.02 0.08 4000 0.10 C.3用曼彻斯特码型重做C.2步并记录结果。 表3.3 曼彻斯特码 sigma bw A 3000 0.01 2000 1000 0.02 0.08 4000 0.10 问题3.4在sigma=0.01和b.=1000的情况下,比较C.2和C.3眼图,你认为哪一个 码型有“较好的”眼图?并根据码型各自的优点来解释这种现象! C.4按照步骤C.2分别用双极性归零码,单极性归零码和单极性不归零码来产生眼图,并观察 码型是如何确定眼图的形状和对称性的。 -20
―20― 最佳抽样时刻 t *是眼图中张开最大处的时间,如在图 3.3 中,t *为 0.0008 秒。如果二进 制码周期为 Tb ,那么为了进行信号检测,我们将在 t * ,t*+Tb ,t*+2Tb 等处对波形抽样,然后 利用这些判决值进行判决。请采用双极性不归零波形产生一个眼图,噪声功率 sigma 和 信道带宽 bw 显示在表 3.2 中,对每一组 sigma、bw,记录 t*、A、B 的值(提示:将不同 的噪声功率 sigma 和信道带宽 bw代入函数 y=channel(x,1,sigma,bw)中即可)。 表 3.2 双极性不归零码 sigma bw t* A B 3000 2000 0.01 1000 0.02 0.08 0.10 4000 C.3 用曼彻斯特码型重做 C.2 步并记录结果。 表 3.3 曼 彻 斯 特 码 sigma bw t* A B 3000 2000 0.01 1000 0.02 0.08 0.10 4000 问题 3.4 在 sigma=0.01 和 bw=1000 的情况下,比较 C.2 和 C.3 眼图,你认为哪一个 码型有“较好的”眼图?并根据码型各自的优点来解释这种现象! C.4 按照步骤 C.2 分别用双极性归零码,单极性归零码和单极性不归零码来产生眼图,并观察 码型是如何确定眼图的形状和对称性的

实验四【 匹配滤波器信号检测 [实验目的]: 在这个实验中,你将学习到以下内容 ●观察匹配滤波器的特性。 ●通过测量误码率来研究基于不同滤波器的接收机的性能。 ●用眼图来设置检测过程中的参数。 [参考文献]: 1.沈振元等,“通信系统原理”,西安电子科技大学出版社,1993 2.曹志刚.钱亚生.“现代通信原理”清华大学出版社.1992 3.王立宁等编,“MATLAB与通信仿真”,人民邮电出版社,2000 [预习作业] 1.讨论用来检测方波r0=ec一工。凸)的匹配滤波器T,=1ms: 如果(0是输 确定匹配 滤波器的输 c.对一个码元周期为10ms的三角波重复a,b。 2.设))叶O,代表信道输出的波形。0是单位幅度的双极性不归零波形,且码率 R,为1kbps。n()是一个功率谱密度为: S(f)=N。/2=0.5×104W1H 的白噪声过程。如果通讨一匹配滤波器: a确定E,(即一比特期间X)的平均能量)。 b.确定在匹配滤波器输出端信号幅度的峰值和噪声的均方值。 c确定误比特率户=Q(,不,)《Q)-方,函最咏可以用 MATLAB计算。) -21
―21― 实验四 匹配滤波器信号检测 [实验目的]: 在这个实验中,你将学习到以下内容: l 观察匹配滤波器的特性。 l 通过测量误码率来研究基于不同滤波器的接收机的性能。 l 用眼图来设置检测过程中的参数。 [参考文献]: 1. 沈振元等,“通信系统原理”,西安电子科技大学出版社,1993 2. 曹志刚,钱亚生,“现代通信原理”,清华大学出版社,1992 3. 王立宁等编,“MATLAB 与通信仿真”,人民邮电出版社,2000 [预习作业] 1. 讨论用来检测方波 ) / 2 ( ) ( b b T t T r t rect - = 的匹配滤波器(Tb=1ms): a. 确定匹配滤波器的脉冲响应波形。 b. 如果 r(t)是输入,确定匹配滤波器的输出。 c. 对一个码元周期为 10ms 的三角波重复 a,b。 2. 设 Y(t)=X(t)+n(t),代表信道输出的波形。X(t)是单位幅度的双极性不归零波形,且码率 Rb 为 1 kbps。n(t)是一个功率谱密度为: S f N W Hz n ( ) / 2 0.5 10 / 4 0 - = = ´ 的白噪声过程。如果 Y(t)通过一匹配滤波器: a. 确定 Eb (即一比特期间 X(t)的平均能量)。 b. 确定在匹配滤波器输出端信号幅度的峰值和噪声的均方值。 c. 确定误比特率: ) 2 ( N 0 E P Q b e = ,( ) 2 ( 2 1 ( ) x Q x = erfc ,函数 erfc 可以用 MATLAB 计算。)