
1,不包含任何字符(长度为)的串称为空串:由一个或多个空格(仅由空格符)组成的串称 为空白串。 (对应严题集4.1①,简答:简述空串和空格串的区别) 2.设S=“A/documen/Mary.doc”,,则strlen(s) 20 的字符定位的位置为3。 3.设日标T=”abccdedccbaa”,模式P=“cdcc”,则第6次匹配成功。 4假设有一维数组Axg,每个元素用相邻的6个字节存储,存储婴按字带编址。已知A的起始存储位置 (基地址)为 00, A的体积(存储量) 末尾元素A7的第 1282 :若按行存储时,元系A4的第 一个字节地址为(8+4)×6+1000=1072:若按列存储时,元 素A47的第一个字节地址为_(6×7+4)×6+1000)=1276 (注:数组是从0行0列还是从1行1列计算起呢?由末单元为A57可知,是从0行0列开始1 5.设数组[160,1.70]的基地址为2048,每个元素占2个存储单元,若以列序为主序顺序存储,则元素 储地 LOC(a)=LOC(ae1,c2)+[(j-c2)*(di-c+I)+i-cI* 得:L0C(a2,58)=2048+(58-1)*(60-1+1)+32-1*2=8950 6.三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分别表示该元素 的行下标 列下标和元素值 10.求下列广义表操作的结果 GetHead【(a,b,(c,d)】 (a.b) ∥头元素不必加括号 (2)GetHead【GetTail【(a,b).(c,d)】==(c.d (3)GetHead【GetTail【GetHead【(a,b,(c,d)JJ】=b (4)GetTail【gethead【GetTail【(a b)(c d)】】】==(d) (B)1.串是一种特殊的线性表 ,其特殊性体现在 A,可以顺序存储 B.数据元素是一个字符 C,可以链式存储 D。数据元素可以是多个字符 (D)2.设串sl='ABCDEFG',s2='PQRST,函数con(x.y)返回x和y串的连接串,subs(s,.i,j)返回串s 的从序号i开始的j个字符组成的子串,len(s)返回串s的长度,则con(subs(sl,2,len(s2)subs(sl,lens2),2)》 的结果串是 BCDE B.BCDEFG C.BCPQRST D.BCDEFE 解:con(x.y)返回x和y串的连接串,即con(Xy)=‘ABCDEFGPQRST': subs1,j)返回串s的从序号i开始的j个字符组成的子串,则 subs(s1.2,len(s2))=subs(sl,2.5)='BCDEF'subs(sl,len(s2).2)=subs(s1,5,2)='EF' 所以con(subs(sI,2,len(s2.ubsl,len(s2,.2)=con'BCDEF','EF')之连接,即BCDEFEF (A)3.假设有60行70列的二维数组a[160,170]以列序为主序顺序存储,其基地址为10000,每 个元素占2个存储单元,那么第32行第58列的元素32,58)的存储地址为 ·(无第0行第0列元素) A.16902B.16904 C.14454 D.答案A,B,C均不对 答:(57列×60行+31行)×2字节+10000=16902 (B4.设矩阵A是一个对称矩阵,为了节省存储,将其下三角部分(如下图所示)按行序存放在一维 数组B[1,(-I)/2]中,对下三角部分中任一元素a(≤j),在一维数组B中下标k的值是:
1 1. 不包含任何字符(长度为 0)的串 称为空串; 由一个或多个空格(仅由空格符)组成的串 称 为空白串。 (对应严题集 4.1①,简答题:简述空串和空格串的区别) 2. 设 S=“A;/document/Mary.doc”,则 strlen(s)= 20 , “/”的字符定位的位置为 3 。 3. 设目标 T=”abccdcdccbaa”,模式 P=“cdcc”,则第 6 次匹配成功。 4. 假设有二维数组 A6×8,每个元素用相邻的 6 个字节存储,存储器按字节编址。已知 A 的起始存储位置 (基地址)为 1000,则数组 A 的体积(存储量)为 288 B ;末尾元素 A57 的第一个字节地址为 1282 ;若按行存储时,元素 A14 的第一个字节地址为 (8+4)×6+1000=1072 ;若按列存储时,元 素 A47 的第一个字节地址为 (6×7+4)×6+1000)=1276 。 (注:数组是从 0 行 0 列还是从 1 行 1 列计算起呢?由末单元为 A57 可知,是从 0 行 0 列开始!) 5.设数组 a[1.60, 1.70]的基地址为 2048,每个元素占 2 个存储单元,若以列序为主序顺序存储,则元素 a[32,58]的存储地址为 8950 。 答:不考虑 0 行 0 列,利用列优先公式: LOC(aij)=LOC(ac1,c2 )+[(j-c2)*(d1-c1+1)+i-c1)]*L 得:LOC(a32,58)=2048+[(58-1)*(60-1+1)+32-1]]*2=8950 6. 三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分别表示该元素 的 行下标 、 列下标 和 元素值 。 10.求下列广义表操作的结果: (1) GetHead【((a,b),(c,d))】=== (a, b) ; //头元素不必加括号 (2) GetHead【GetTail【((a,b),(c,d))】】=== (c,d) ; (3) GetHead【GetTail【GetHead【((a,b),(c,d))】】】=== b ; (4) GetTail【GetHead【GetTail【((a,b),(c,d))】】】=== (d) ; ( B )1.串是一种特殊的线性表,其特殊性体现在: A.可以顺序存储 B.数据元素是一个字符 C.可以链式存储 D.数据元素可以是多个字符 ( D )2.设串 s1=’ABCDEFG’,s2=’PQRST’,函数 con(x,y)返回 x 和 y 串的连接串,subs(s, i, j)返回串 s 的从序号 i 开始的 j 个字符组成的子串,len(s)返回串 s 的长度,则 con(subs(s1, 2, len(s2)), subs(s1, len(s2), 2)) 的结果串是: A.BCDEF B.BCDEFG C.BCPQRST D.BCDEFEF 解:con(x,y)返回 x 和 y 串的连接串,即 con(x,y)=‘ABCDEFGPQRST’; subs(s, i, j)返回串 s 的从序号 i 开始的 j 个字符组成的子串,则 subs(s1, 2, len(s2))=subs(s1, 2, 5)=’ BCDEF’; subs(s1, len(s2), 2)=subs(s1, 5, 2)=’ EF’; 所以 con(subs(s1, 2, len(s2)), subs(s1, len(s2), 2))=con(’ BCDEF’, ’ EF’)之连接,即 BCDEFEF ( A )3.假设有 60 行 70 列的二维数组 a[1.60, 1.70]以列序为主序顺序存储,其基地址为 10000,每 个元素占 2 个存储单元,那么第 32 行第 58 列的元素 a[32,58]的存储地址为 。(无第 0 行第 0 列元素) A.16902 B.16904 C.14454 D.答案 A, B, C 均不对 答:(57 列×60 行+31 行)×2 字节+10000=16902 ( B )4. 设矩阵 A 是一个对称矩阵,为了节省存储,将其下三角部分(如下图所示)按行序存放在一维 数组 B[ 1, n(n-1)/2 ]中,对下三角部分中任一元素 ai,j(i≤j), 在一维数组 B 中下标 k 的值是:

A.i-1)/2+-1B.ii-1)2+j C.i0i+1)2+j-1 D.ii+1)/2+i 「au 解:注意B的下标要求从1开始。 先用第一个元素去套用,可能有B和C: 再用第二个元素去套用B和C,B=2而C=3(不符) 所以选B 1.用三元组表表示下列稀疏矩阵: 00000000 00000000 「00000-2 03000800 000090 00000000 ( (2)/00000 0 00060000 005000 00000000 000000 00000005 [000030 20000000 解:参见填空题4.三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分 别表示该元素的行下标 列下标 和元素值 所以(1)可列表为 (2)可列表为: 5 6 6 4 5 5 3 1 2 解:(1)为6×4矩阵,非零元素有6个。 (2)为4×5矩阵,非零元素有5个 1.设一棵完全二叉树有700个结点,则共有350个叶子结点。 答:最快方法:用叶子数=/21=350 2设一棵完全二叉树具有1000个结点,则此完全二叉树有500个叶子结点,有499个度为2的结 点,有1 个结点只有非空左子树,有0 个结 点只有非空右子树 答:最快方法:用叶子数=1/2=500,-1-499。另外,最后一结点为2i属于左叶子,右叶子是空 的,所以有1个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况,所以非空右子树数=心 3.一棵含有n个结点的k叉树,可能达到的最大深度为n,最小深度为2。 答:当k-1(单叉树时应该最深,深度=n(层)当k-1(-1叉树)时应该最浅,深度=2(层),但不 包括 -0或 时的特例情况 “完全k叉树”,未定量。) 4.用5个权值{3,2,4,5,1)构造的哈夫曼(Huffman)树的带权路径长度是_ 55 解:先构造哈夫曼树,得到各叶子的路径长度之后便可求出WPL=(4十5十3)×2十(1十2)×3=33 15) 160 (注:两个合并值先后不同会导致编码不同,即哈夫曼编码不唯一) (注:合并值应排在叫 子值之后) 2
2 A.i(i-1)/2+j-1 B.i(i-1)/2+j C.i(i+1)/2+j-1 D.i(i+1)/2+j 1.用三元组表表示下列稀疏矩阵: 20000000 00000005 00000000 00060000 00000000 03000800 00000000 00000000 (1) − 00003 0 00000 0 00500 0 00000 0 00009 0 00000 2 (2) 解:参见填空题 4. 三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分 别表示该元素的 行下标 、 列下标 和 元素值 。 所以(1)可列表为: (2)可列表为: 8 8 5 3 2 3 3 6 8 5 4 6 7 8 5 8 1 2 解:(1)为 6×4 矩阵,非零元素有 6 个。 (2)为 4×5 矩阵,非零元素有 5 个 1.设一棵完全二叉树有 700 个结点,则共有 350 个叶子结点。 答:最快方法:用叶子数=[n/2]=350 2.设一棵完全二叉树具有 1000 个结点,则此完全二叉树有 500 个叶子结点,有 499 个度为 2 的结 点,有 1 个结点只有非空左子树,有 0 个结点只有非空右子树。 答:最快方法:用叶子数=[n/2]=500 ,n2=n0-1=499。 另外,最后一结点为 2i 属于左叶子,右叶子是空 的,所以有 1 个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况,所以非空右子树数=0. 3. 一棵含有 n 个结点的 k 叉树,可能达到的最大深度为 n ,最小深度为 2 。 答:当 k=1(单叉树)时应该最深,深度=n(层);当 k=n-1(n-1 叉树)时应该最浅,深度=2(层),但不 包括 n=0 或 1 时的特例情况。教材答案是“完全 k 叉树”,未定量。) 4. 用 5 个权值{3, 2, 4, 5, 1}构造的哈夫曼(Huffman)树的带权路径长度是 33 。 解:先构造哈夫曼树,得到各叶子的路径长度之后便可求出 WPL=(4+5+3)×2+(1+2)×3=33 (15) (9) (6) (注:两个合并值先后不同会导致编码不同,即哈夫曼编码不唯一) 4 5 3 (3) (注:合并值应排在叶子值之后) 1 2 6 6 4 1 6 -2 2 5 9 4 3 5 6 5 3 解:注意 B 的下标要求从 1 开始。 先用第一个元素去套用,可能有 B 和 C; 再用第二个元素去套用 B 和 C,B=2 而 C=3(不符); 所以选 B = an an an n a a a A ,1 ,2 , 2,1 2,2 1,1

(注:原题为选择题:A.32 B.33 C.34D.15) (C)1,不含任何结点的空树 CA)是 (B)是一棵二叉树 (D)既不是树也不是二叉树 答:以前的标答是B,因为那时树的定义是n≥1 (C)2.二叉树是非线性数据结构,所以 (A)它不能用顺序存储结构存储 (B)它不能用僻式存储结构存储: (C)顺序存储结构和链式存储结构都能存储 (D)顺序存储结构和链式存储结构都不能使 用 (C)3.具有n(>0)个结点的完全二叉树的深度为 (A)Tlogz(n)1 (B)L logz(n)(C)L logz(n)1 (D)[logz(n)+17 注1:「x表示不小于x的最小整数:Lx表示不大于x的最大整数,它们与]含义不同! 注2:选(A)是错误的。例如当n为2的整数幂时就会少算一层。似平乳log(+1是对的 (A)4,把一棵树转换为二叉树后,这棵二叉树的形态是 (A)唯一的 (B)有多种 (C)有多种,但根结点都没有左孩子(D)有多种,但根结点都没有右孩子 5。【94程P1】从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写 在答卷的对应栏内。 树是结点的有限集合,它A根结点,记为T。其余的结点分成为m(m≥0)个B 的集合T1,T2,Tm,每个集合又都是树,此时结点T称为T的父结点,T称为T的子结点(1≤i 个结点的子结点个数为该结点的C 供选择的答案 A:①有0个或1个 ②有0个或多个 ③有且只有1个 ④有1个或1个以上 B:①互不相交 ②允许相交 ③允许叶结点相交④允许树枝结点相交 C:①权 ②维数 ⑧次数(或度) ④序 答案:ABC=1,1,3 6【95程P13】从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在 答卷的对应栏内。 二叉树人。在完全的二叉树中,若一个结点没有B,则它必定是叶结点。每棵树都能惟一地 转换成与它对应的二叉树,由树转换成的二叉树里,一 个结点N的左子女是N在原树里对应结点的C 而N的右子女是它在原树里对 应结点的D 供透择的答案 A:①是特殊的树②不是树的特殊形式③是两棵树的总称④有是只有二个根结点的树形结构 B:①左子结点②右子结点回左子结点或者没有右子结点④兄弟 C~D:①最左子结点 ②最右子结点⑨最邻近的右兄弟 ④最邻近的左兄弟 最左的兄弟 ®最右的兄弟 答案 A D= 答案:ABCDE=2,1,1,3 2
3 (注:原题为选择题:A.32 B.33 C.34 D.15) ( C )1. 不含任何结点的空树 。 (A)是一棵树; (B)是一棵二叉树; (C)是一棵树也是一棵二叉树; (D)既不是树也不是二叉树 答:以前的标答是 B,因为那时树的定义是 n≥1 ( C )2.二叉树是非线性数据结构,所以 。 (A)它不能用顺序存储结构存储; (B)它不能用链式存储结构存储; (C)顺序存储结构和链式存储结构都能存储; (D)顺序存储结构和链式存储结构都不能使 用 ( C )3. 具有 n(n>0)个结点的完全二叉树的深度为 。 (A) log2(n) (B) log2(n) (C) log2(n) +1 (D) log2(n)+1 注 1:x 表示不小于 x 的最小整数; x表示不大于 x 的最大整数,它们与[ ]含义不同! 注 2:选(A)是错误的。例如当 n 为 2 的整数幂时就会少算一层。似乎log2(n) +1是对的? ( A )4.把一棵树转换为二叉树后,这棵二叉树的形态是 。 (A)唯一的 (B)有多种 (C)有多种,但根结点都没有左孩子 (D)有多种,但根结点都没有右孩子 5. 【94 程 P11】 从供选择的答案中,选出应填入下面叙述 ? 内的最确切的解答,把相应编号写 在答卷的对应栏内。 树是结点的有限集合,它 A 根结点,记为 T。其余的结点分成为 m(m≥0)个 B 的集合 T1,T2,.,Tm,每个集合又都是树,此时结点 T 称为 Ti的父结点,Ti 称为 T 的子结点(1≤i ≤m)。一个结点的子结点个数为该结点的 C 。 供选择的答案 A: ①有 0 个或 1 个 ②有 0 个或多个 ③有且只有 1 个 ④有 1 个或 1 个以上 B: ①互不相交 ② 允许相交 ③ 允许叶结点相交 ④ 允许树枝结点相交 C: ①权 ② 维数 ③ 次数(或度) ④ 序 答案:ABC=1,1,3 6. 【95 程 P13】 从供选择的答案中,选出应填入下面叙述 ? 内的最确切的解答,把相应编号写在 答卷的对应栏内。 二叉树 A 。在完全的二叉树中,若一个结点没有 B ,则它必定是叶结点。每棵树都能惟一地 转换成与它对应的二叉树。由树转换成的二叉树里,一个结点 N的左子女是 N在原树里对应结点的 C , 而 N 的右子女是它在原树里对应结点的 D 。 供选择的答案 A: ①是特殊的树 ②不是树的特殊形式 ③是两棵树的总称 ④有是只有二个根结点的树形结构 B: ①左子结点 ② 右子结点 ③ 左子结点或者没有右子结点 ④ 兄弟 C~D: ①最左子结点 ② 最右子结点 ③ 最邻近的右兄弟 ④ 最邻近的左兄弟 ⑤ 最左的兄弟 ⑥ 最右的兄弟 答案:A= B= C= D= 答案:ABCDE=2,1,1,3

2.【01年计算机研题〗设如下图所示的二叉树B的存储结构为二叉链表,rOt为根指针,结点结构为: (Ichild,.data,rchild),其中Ichild,rchild分别为指向左右孩子的指针, daa为字符型,o0t为根指针,试回答下列问题 C的结点类型定义如下: .对下列二叉树B,执行下列算法traversa(root),试指出其输出结 struct node char data: 果: 2.假定二叉树B共有n个结点,试分析算法traversal(roc)的时间复 struct node*lchild,rchild: 杂度。(共8分) C算法如下: void traversal(struct node *root) if(root) 二叉树B G E printf"%c"root->data) 解:这是“先根再左再根再右”,比前序遍历多打印各结点一次,输 traversal(root-lchild) 出结果为:ABCCEEBADFFDG( printf(%c”,root data) 特点:①每个结点肯定都会被打印两次:②但出现的顺序不同,其 traversal(root->rchild). 规律是:凡是有左子树的结点,必间隔左子树的全部结点后再重复 出现:如A,B,D等结点。反之马上就会重复出现。如C,E,F, G竺结占 时间复杂度以访问结点的次数为主,精确值为2,时间渐近度为O(m) 【01年计算机研题】【严题集6.27③】给定二叉树的两种遍历序列,分别是: 前序遍历序列:D,A,C,E,B,H,F,G,I: 中序遍历序列:D,C,B,E,H,A,G,I,F, 试画出二叉树B,并简述由任意二叉树B的前序遍历序列和中序遍历序列求二叉树B的思想方法。 解:方法是:由前序先确定roo,由中序可确定rot的左、右子树。然后由其左子树的元素集合和右子 树的集合对应前序历序列中的元素集合,可继续确定rot的左右孩子。将他们分别作为新的r,不 断递归,则所有元素都将被唯一确定,问题得解 A 五、阅读分析题(每题5分,共20分) 1.(P604-26)试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列 答:DLR:ABDFJGKCEHILM LDR BEJDGKACHELIM Lrd:FKGDBHLMIECA 2.(P604-27)把如图所示的树转化成二叉树。 答:注意全部兄弟之间都要讳线(包括度为2的只 ) ,并注意原有连线结点一律归入左子树,新添
4 2.〖01 年计算机研题〗设如下图所示的二叉树 B 的存储结构为二叉链表,root 为根指针,结点结构为: (lchild,data,rchild)。其中 lchild,rchild 分别为指向左右孩子的指针, data 为字符型,root 为根指针,试回答下列问题: 1. 对下列二叉树 B,执行下列算法 traversal(root),试指出其输出结 果; 2. 假定二叉树 B 共有 n 个结点,试分析算法 traversal(root)的时间复 杂度。(共 8 分) 二叉树 B 解:这是“先根再左再根再右”,比前序遍历多打印各结点一次,输 出结果为:A B C C E E B A D F F D G G 特点:①每个结点肯定都会被打印两次;②但出现的顺序不同,其 规律是:凡是有左子树的结点,必间隔左子树的全部结点后再重复 出现;如 A,B,D 等结点。反之马上就会重复出现。如 C,E,F, G 等结点。 时间复杂度以访问结点的次数为主,精确值为 2*n,时间渐近度为 O(n). 3. 〖01 年计算机研题〗【严题集 6.27③】给定二叉树的两种遍历序列,分别是: 前序遍历序列:D,A,C,E,B,H,F,G,I; 中序遍历序列:D,C,B,E,H,A,G,I,F, 试画出二叉树 B,并简述由任意二叉树 B 的前序遍历序列和中序遍历序列求二叉树 B 的思想方法。 解:方法是:由前序先确定 root,由中序可确定 root 的左、右子树。然后由其左子树的元素集合和右子 树的集合对应前序遍历序列中的元素集合,可继续确定 root 的左右孩子。将他们分别作为新的 root,不 断递归,则所有元素都将被唯一确定,问题得解。 D A C F E G B H I 五、阅读分析题(每题 5 分,共 20 分) 1. (P60 4-26)试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列。 答:DLR:A B D F J G K C E H I L M LDR: B F J D G K A C H E L I M LRD:J F K G D B H L M I E C A 2. (P60 4-27)把如图所示的树转化成二叉树。 答:注意全部兄弟之间都要连线(包括度为 2 的兄 弟),并注意原有连线结点一律归入左子树,新添 A B D C F G E C 的结点类型定义如下: struct node {char data; struct node *lchild, rchild; }; C 算法如下: void traversal(struct node *root) {if (root) {printf(“%c”, root->data); traversal(root->lchild); printf(“%c”, root->data); traversal(root->rchild); } }
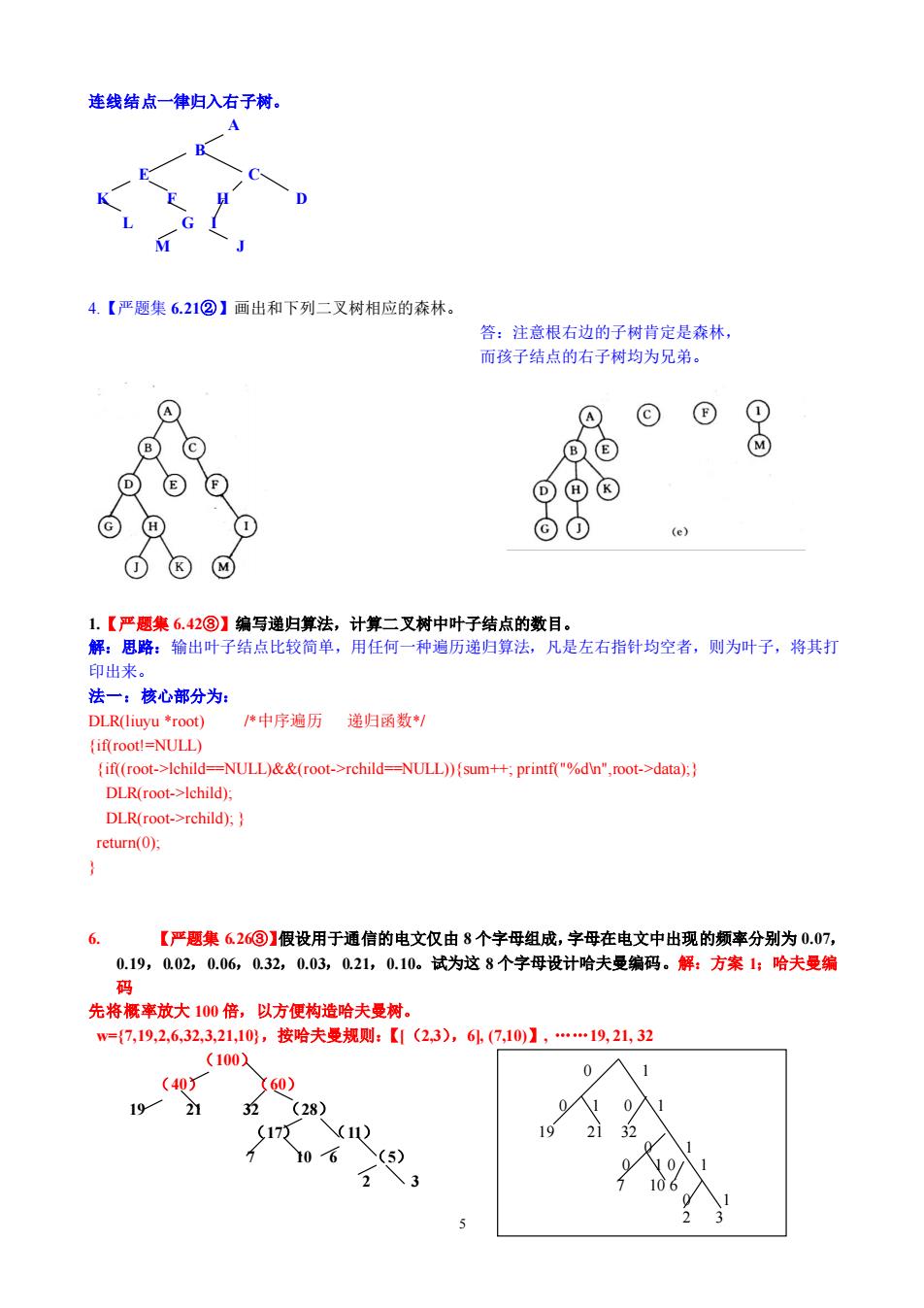
连线结点一律归入右子树。 A 4.【严题集6.21②】画出和下列二叉树相应的森林 答:注意根右边的子树肯定是森林, 而孩子结点的右子树均为兄弟。 ⊙ ⊙ ⊙⑧⑧ ⊙① (e) 1.【严题集6.42③】编写递归算法,计算二叉树中叶子结点的数目。 解:思路:输出叶子结点比较简单,用任何一种遍历递归算法,凡是左右指针均空者,则为叶子,将其打 印出来。 法一:核心部分为: DLR(liuyu *root) 体中序遍历递归函数制 (if(rootl=NULL) {if((root->Ichild=NULL&&(root->rchild=NULL))fsum++;printf("%dVn",root->data): DLR(root->Ichildy DLR(root->rehild). return(); 6. 【严题集626③】假设用于通信的电文仅由8个字母组成,半母在电文中出现的频率分别为0.07 0.19,Q.02,0.06,0.32,0.03,0.21,0.10。试为这8个字母设计哈夫曼编码。解:方案1:哈夫曼编 码 先将概率放大10倍,以方便构造哈夫曼树。 W=7,192,6.32,3,21.10,按哈夫曼规则:【(2,3),61(7,10】,.19,21,32 (1002 0入1 19 21 3(28) S171(1) 9 21 06(5) 2 3
5 连线结点一律归入右子树。 A B E C K F H D L G I M J 4.【严题集 6.21②】画出和下列二叉树相应的森林。 答:注意根右边的子树肯定是森林, 而孩子结点的右子树均为兄弟。 1.【严题集 6.42③】编写递归算法,计算二叉树中叶子结点的数目。 解:思路:输出叶子结点比较简单,用任何一种遍历递归算法,凡是左右指针均空者,则为叶子,将其打 印出来。 法一:核心部分为: DLR(liuyu *root) /*中序遍历 递归函数*/ {if(root!=NULL) {if((root->lchild==NULL)&&(root->rchild==NULL)){sum++; printf("%d\n",root->data);} DLR(root->lchild); DLR(root->rchild); } return(0); } 6. 【严题集 6.26③】假设用于通信的电文仅由 8 个字母组成,字母在电文中出现的频率分别为 0.07, 0.19,0.02,0.06,0.32,0.03,0.21,0.10。试为这 8 个字母设计哈夫曼编码。解:方案 1;哈夫曼编 码 先将概率放大 100 倍,以方便构造哈夫曼树。 w={7,19,2,6,32,3,21,10},按哈夫曼规则:【[(2,3),6], (7,10)】, .19, 21, 32 (100) (40) (60) 19 21 32 (28) (17) (11) 7 10 6 (5) 2 3 0 1 0 1 0 1 19 21 32 0 1 0 1 0 1 7 10 6 0 1 2 3