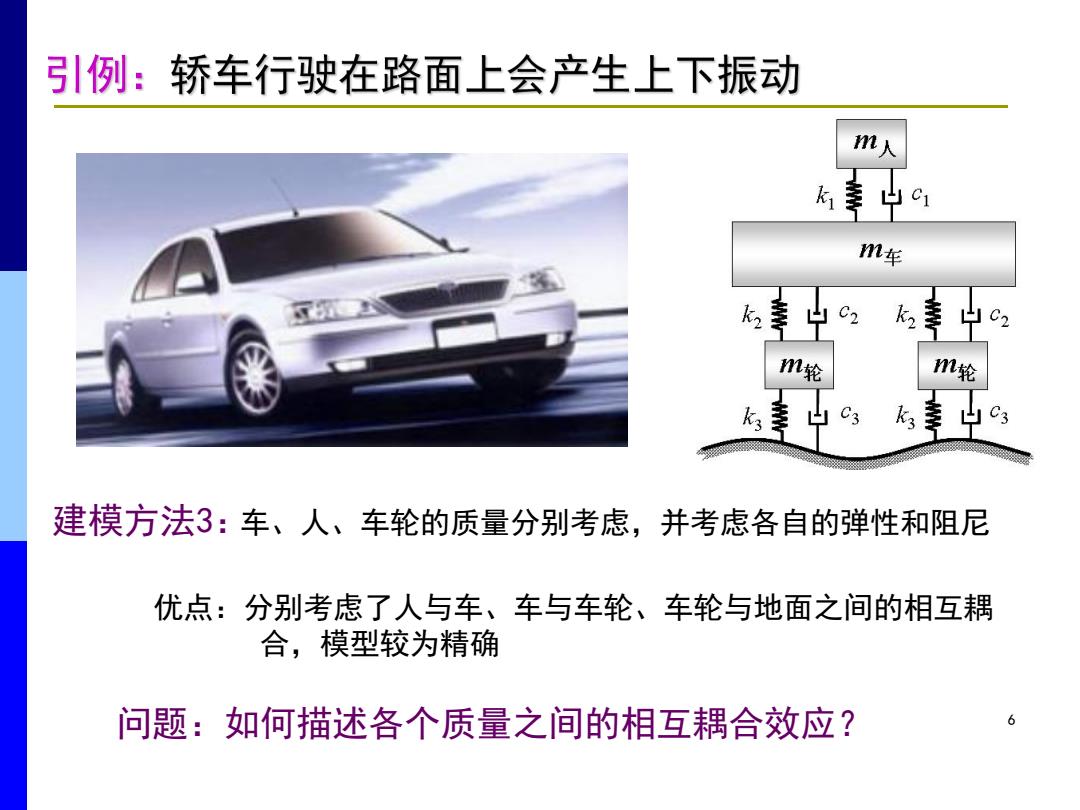
引例:轿车行驶在路面上会产生上下振动 m人 车 m轮 m轮 建模方法3:车、人、车轮的质量分别考虑,并考虑各自的弹性和阻尼 优点:分别考虑了人与车、车与车轮、车轮与地面之间的相互耦 合,模型较为精确 问题:如何描述各个质量之间的相互耦合效应? 6
6 建模方法3: 优点:分别考虑了人与车、车与车轮、车轮与地面之间的相互耦 合,模型较为精确 问题:如何描述各个质量之间的相互耦合效应? 车、人、车轮的质量分别考虑,并考虑各自的弹性和阻尼

主要内容 口多自由度系统的动力学方程 作用力方程(刚度矩阵质量矩阵) 位移方程(柔度矩阵) 耦合与坐标变换 口多自由度系统的自由振动 固有频率 模态(主振型) 模态正交性、主质量和主刚度 口多自由度系统的受迫振动 系统对简谐力激励的响应 动力吸振器 7 模态叠加法在受迫振动中的应用
7 主要内容

一、 多自由度系统的动力学方程 作用力方程(平动运动和转动运动) 位移方程 8
8

一、多自由度系统的动力学方程一 作用力方程 平动运动。图示双质量弹簧系统,两质量m,和m2分别受到激振 力P()和P()的作用。不计摩擦和其他形式的阻尼,试建立系 统的运动微分方程。 (t0→x K 解:建立坐标: x1,x2的原点分别取在m1,m2的静平衡位置 设某一瞬时:m和m2上分别有位移x1和x2、加速度x2
9 平动运动。图示双质量弹簧系统,两质量m1和m2分别受到激振 力P1(t)和P2(t)的作用。不计摩擦和其他形式的阻尼,试建立系 统的运动微分方程。 m1和m2上分别有位移x1和x2 1 2 设某一瞬时: 、加速度 x、x 解: , 1 x 2 x 的原点分别取在 的静平衡位置 建立坐标: 1 2 m ,m

一、多自由度系统的动力学方程一 作用力方程 P()→ P,(t) 受力分析: P(0 P(t) k2(x1-X) k2(x1-X》 m m22 建立方程: m+kx+k (x-x2)=P(t) 力量纲 m22-k2(x1-x2)+k3x2=P2(t) 10
10 建立方程: 1 1 1 1 2 1 2 1 2 2 2 1 2 3 2 2 ( ) ( ) ( ) ( ) m x k x k x x P t m x k x x k x P t 力量纲 受力分析: