
Example:Payment Prediction Revisit o Find the mapping function or model to answer whether one's salary is more than 50k. Age Edu.year HoursPerWeek Pay 25 7 40 <50k 38 9 50 ≥50k 28 12 40 ≥50k 24 10 40 <50k 55 4 10 ?
• Find the mapping function or model to answer whether one’s salary is more than 50k. Example: Payment Prediction Revisit Age Edu. year HoursPerWeek Pay 25 7 40 <50k 38 9 50 ≥50k 28 12 40 ≥50k 24 10 40 <50k 55 4 10 ?
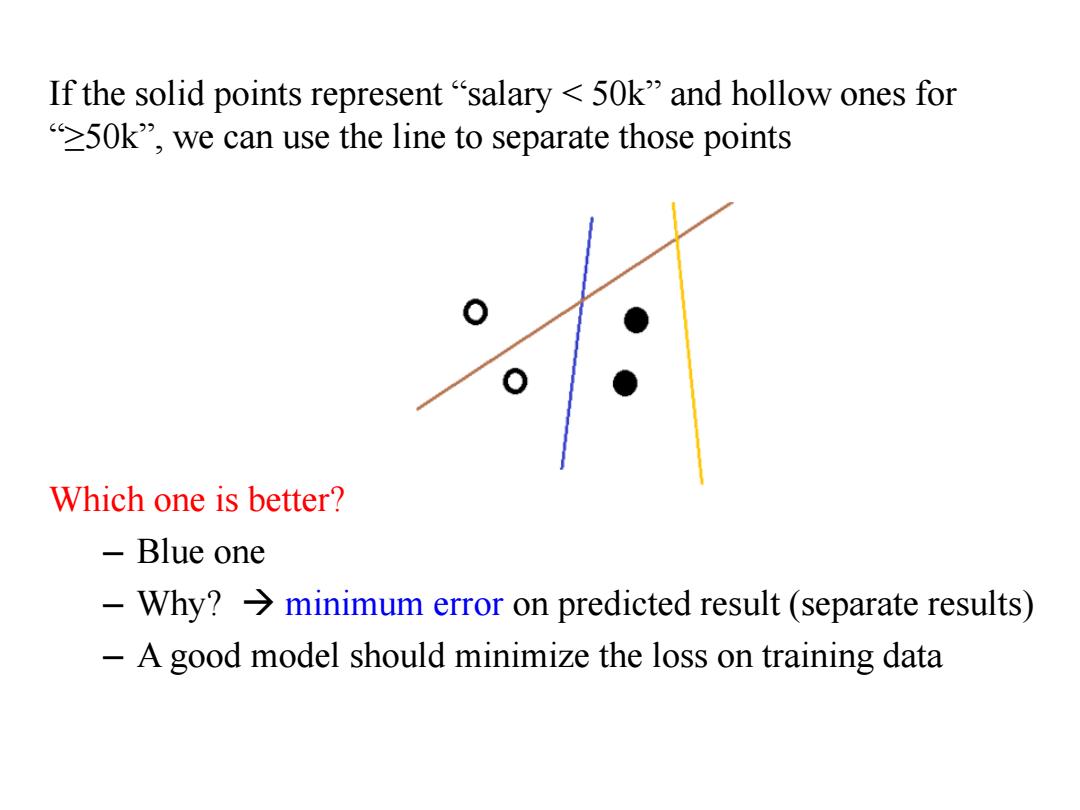
If the solid points represent"salary 50k"and hollow ones for 50k",we can use the line to separate those points Which one is better? Blue one -Why?>minimum error on predicted result(separate results) -A good model should minimize the loss on training data
If the solid points represent “salary < 50k” and hollow ones for “≥50k”, we can use the line to separate those points Which one is better? – Blue one – Why? minimum error on predicted result (separate results) – A good model should minimize the loss on training data

LOSS FUNCTION To measure the predicted results,we introduce the loss function L(Y,F(X)),which a non-negative function -0-1 loss 6,w)- y=F(x|8) y+F(x|0) Squared loss L(y,F(x)=(y-F(x8)1 Absolute loss L(y,F(x10))=ly-F(x10)I Log loss L(y,P(ylx,0))=-logP(ylx,0)
To measure the predicted results, we introduce the loss function 𝐿 𝑌, 𝐹 𝑋|𝜃 , which a non-negative function – 0-1 loss – Squared loss – Absolute loss – Log loss LOSS FUNCTION L y, F x = 0, 𝑦 = 𝐹(𝑥|𝜃) 1, 𝑦 ≠ 𝐹(𝑥|𝜃) L y, F x|𝜃 = y − F x|𝜃 2 L y, F x|𝜃 = 𝑦 − 𝐹(𝑥|𝜃) L y, P y|x, 𝜃 = −logP(y|x, 𝜃

Training Loss and Test Loss Training loss:loss on training data Test loss:loss on test data Performance on training data of three models 8 000 )● Performance on training data and test data Who wins? ●
Performance on training data of three models Performance on training data and test data Training Loss and Test Loss Who wins? Training loss: loss on training data Test loss: loss on test data

Generalization Empirical risk: R回-∑6ox》 Note:A good model cannot only take training loss into account and minimize the empirical risk.Instead,improve the model generalization Model Model Model True function True function True function Samples Samples ●Samples Model Selection:To avoid Underfitting and Overfitting
Empirical risk: Note: A good model cannot only take training loss into account and minimize the empirical risk. Instead, improve the model generalization. Generalization R F = 1 N 𝑖=1 𝑁 L yi , F xi Model Selection: To avoid Underfitting and Overfitting