电子科技大学：《先进计算机网络技术》课程教学资源（课件讲稿）Unit 2 Call-level Models and Admission Control

Feng Gang National Laboratory of Communication,UESTC Aug 2017 Ver 1.4 Unit 2 Call-level Models and Admission Control 2616009:Network Traffic Engineering 2:Call-level Models and Admission Control Page.1

2616009: Network Traffic Engineering Feng Gang National Laboratory of Communication, UESTC Aug 2017 Ver 1.4 2: Call-level Models and Admission Control Page.1 Unit 2 Call-level Models and Admission Control

Feng Gang National Laboratory of Communication,UESTC Aug 2017 Ver 1.4 Roadmap Review:Queuing Models for Birth-Death Process Multiservice Loss System and The Stochastic Knapsack 。 Admission Policies Optimization Concept Optimal Complete Partitioning Policies Optimal Coordinate Convex Policies Case Study:Call Admission Control for Multi-service Mobile Networks with Bandwidth Asymmetry between Uplink and Downlink 2616009:Network Traffic Engineering 2:Call-level Models and Admission Control Page.2

2616009: Network Traffic Engineering Feng Gang National Laboratory of Communication, UESTC Aug 2017 Ver 1.4 2: Call-level Models and Admission Control Page.2 Roadmap • Review: Queuing Models for Birth-Death Process • Multiservice Loss System and The Stochastic Knapsack • Admission Policies • Optimization Concept • Optimal Complete Partitioning Policies • Optimal Coordinate Convex Policies • Case Study: Call Admission Control for Multi-service Mobile Networks with Bandwidth Asymmetry between Uplink and Downlink

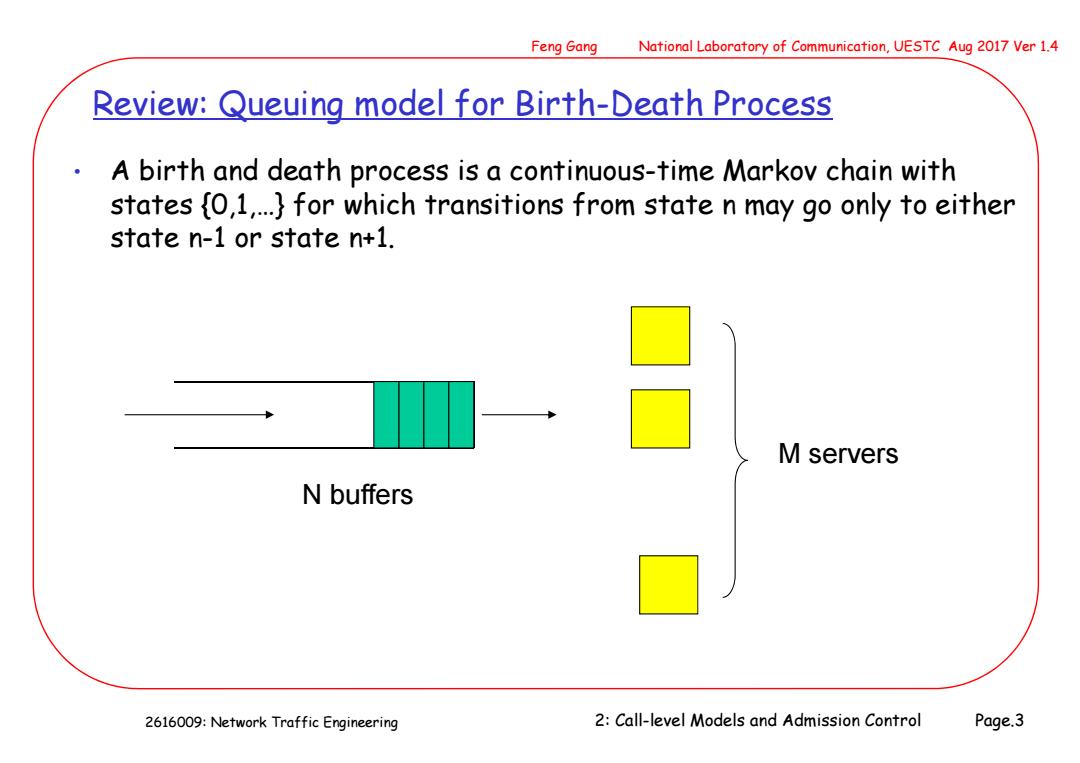
Feng Gang National Laboratory of Communication,UESTC Aug 2017 Ver 1.4 Review:Queuing model for Birth-Death Process A birth and death process is a continuous-time Markov chain with states {0,1,..}for which transitions from state n may go only to either state n-1 or state n+1. M servers N buffers 2616009:Network Traffic Engineering 2:Call-level Models and Admission Control Page.3

2616009: Network Traffic Engineering Feng Gang National Laboratory of Communication, UESTC Aug 2017 Ver 1.4 2: Call-level Models and Admission Control Page.3 Review: Queuing model for Birth-Death Process • A birth and death process is a continuous-time Markov chain with states {0,1,…} for which transitions from state n may go only to either state n-1 or state n+1. N buffers M servers

Feng Gang National Laboratory of Communication,UESTC Aug 2017 Ver 1.4 Queuing model for Birth-Death Process(cont'd) ·Notations -X=number of customers in the system(buffer and servers)at time t -=arrival rate of customers in state X,=n -n =departure rate of customers in state X,=n ·Assumptions P(X+w-X,=1X,=n)=n△t+o(△t) P(X,+-X,=-1|X,=n)=4n△t+o(△) P(X-X,>1X,=n)=0(At) where o(△)=0 o(△)=lim ar 1→0 2616009:Network Traffic Engineering 2:Call-level Models and Admission Control Page.4

2616009: Network Traffic Engineering Feng Gang National Laboratory of Communication, UESTC Aug 2017 Ver 1.4 2: Call-level Models and Admission Control Page.4 Queuing model for Birth-Death Process(cont’d) • Notations - Xt = number of customers in the system (buffer and servers) at time t  n = arrival rate of customers in state  n =departure rate of customers in state • Assumptions Xt  n Xt  n P(X X 1| X n) t o( t) tt  t  t   n   P(X X 1| X n) t o( t) tt  t   t    n   P(| X X | 1| X n) o( t) tt  t  t    where 0 ( ) ( ) lim 0        t o t o t t

Feng Gang National Laboratory of Communication,UESTC Aug 2017 Ver 1.4 Queuing model for Birth-Death Process(cont'd) ·Analysis Let P(t)=P(X,=n) △Pn(t+△t)=Pn(t+△t)-Pn(t) =*P()-()At*P(t)+A*(t) Taking the limit as△t-→o gives Pm(t)）=元n-Pn-1(t)）-(4n+n)Pn(t)+4n+1Pn+1(t) Stationary Conditions P(0)=1 B.=limp(t)P= ∑p=1 -f1a TIa n=1i=0 2616009:Network Traffic Engineering 2:Call-level Models and Admission Control Page.5

2616009: Network Traffic Engineering Feng Gang National Laboratory of Communication, UESTC Aug 2017 Ver 1.4 2: Call-level Models and Admission Control Page.5 Queuing model for Birth-Death Process(cont’d) • Analysis Let P (t) P(X n) n  t  * ( ) ( ) * ( ) * ( ) ( ) ( ) ( ) 1 1 1 1 t P t t P t t P t P t t P t t P t n n n n n n n n n n                       Taking the limit as gives t  o ( ) ( ) ( ) ( ) ( ) 1 1 1 1 ' P t P t P t P t n  n n  n  n n  n n Stationary Conditions P0 (0) 1 ( ) P limP t n t n    nPn  n1Pn1     0 1 i Pi 0 1 0 1 P / P n n n i i                            1 1 0 0 1 1/ 1 / n n i P i i