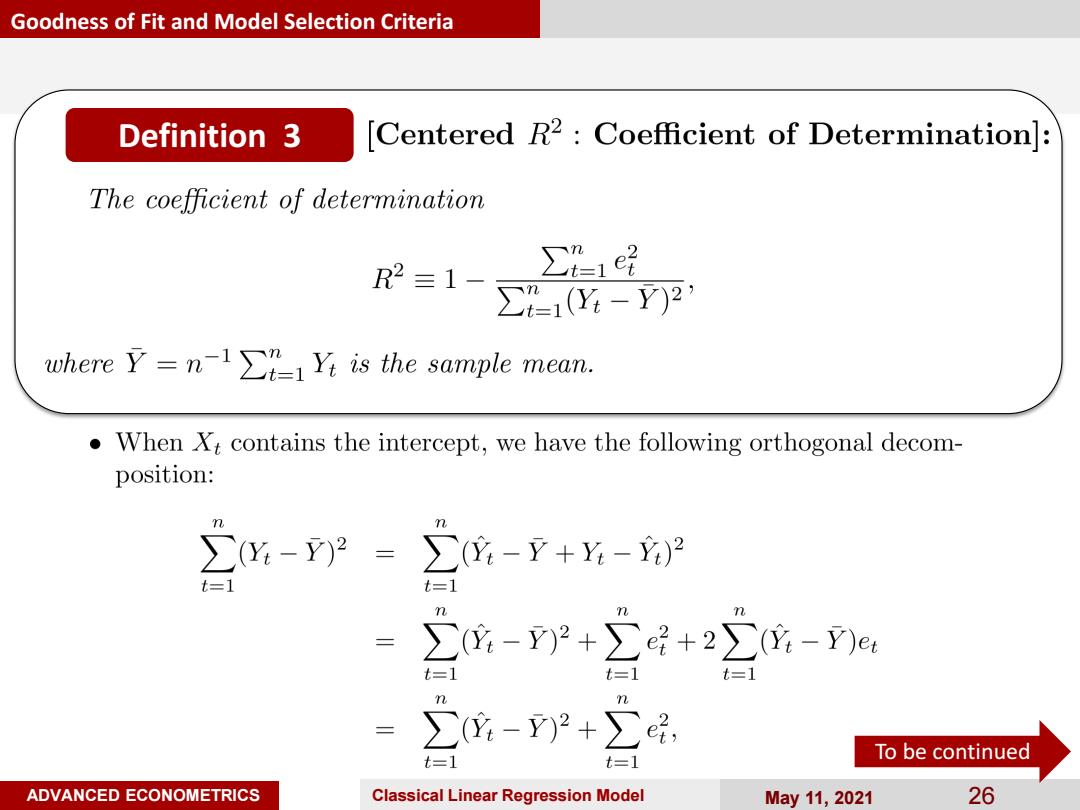
Goodness of Fit and Model Selection Criteria Definition 3 [Centered R2:Coefficient of Determination]: The coefficient of determination R2三1- ∑1经 ∑41(Y-Y)2 where Y=n-1Yi is the sample mean. When Xt contains the intercept,we have the following orthogonal decom- position: 出:-2=∑-+Y-2 t=] t=1 m m ∑2-)2+∑+2∑-Y)e t=1 t=1 t=1 :-YP+∑ t=1 =1 To be continued ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 26
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 26 Goodness of Fit and Model Selection Criteria Definition 3 To be continued
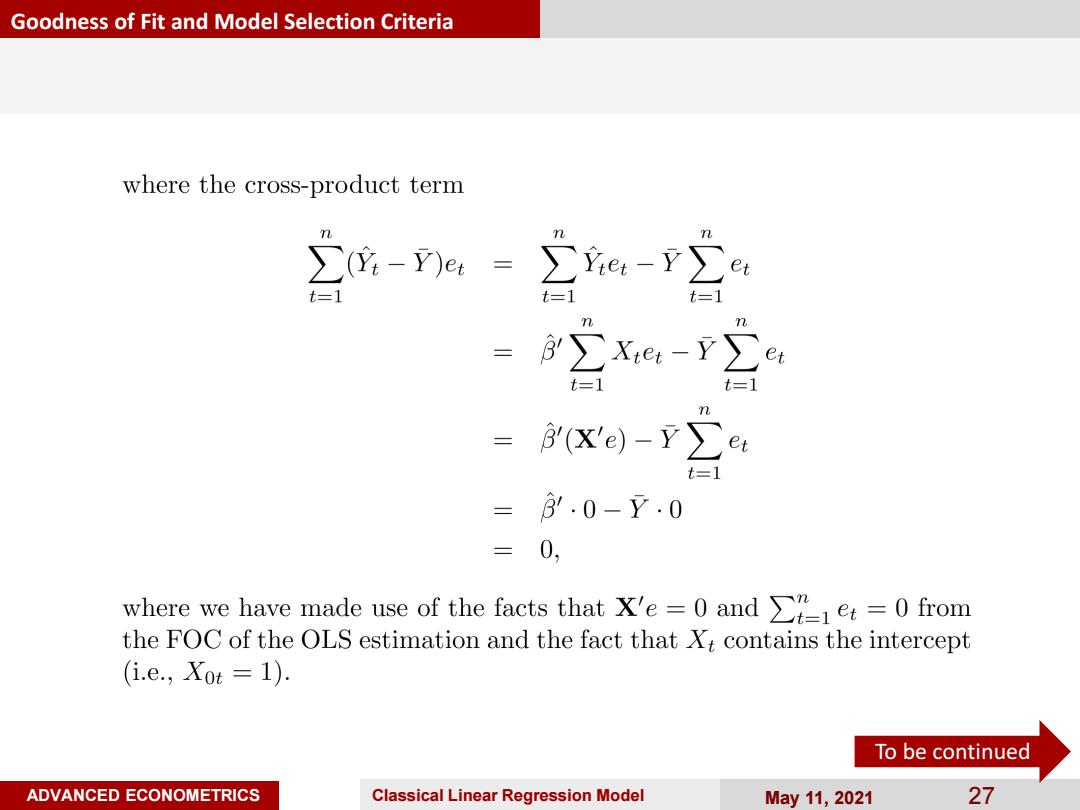
Goodness of Fit and Model Selection Criteria where the cross-product term ∑-Y)e=-∑e:-r∑ t= =∑Xe-y∑e t=1 t=1 = r(x'e)-y∑e t=1 =.0-Y.0 =0, where we have made use of the facts that X'e=0 and e=0from the FOC of the OLS estimation and the fact that Xt contains the intercept (i.e.,X0t=1) To be continued ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 27
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 27 Goodness of Fit and Model Selection Criteria To be continued
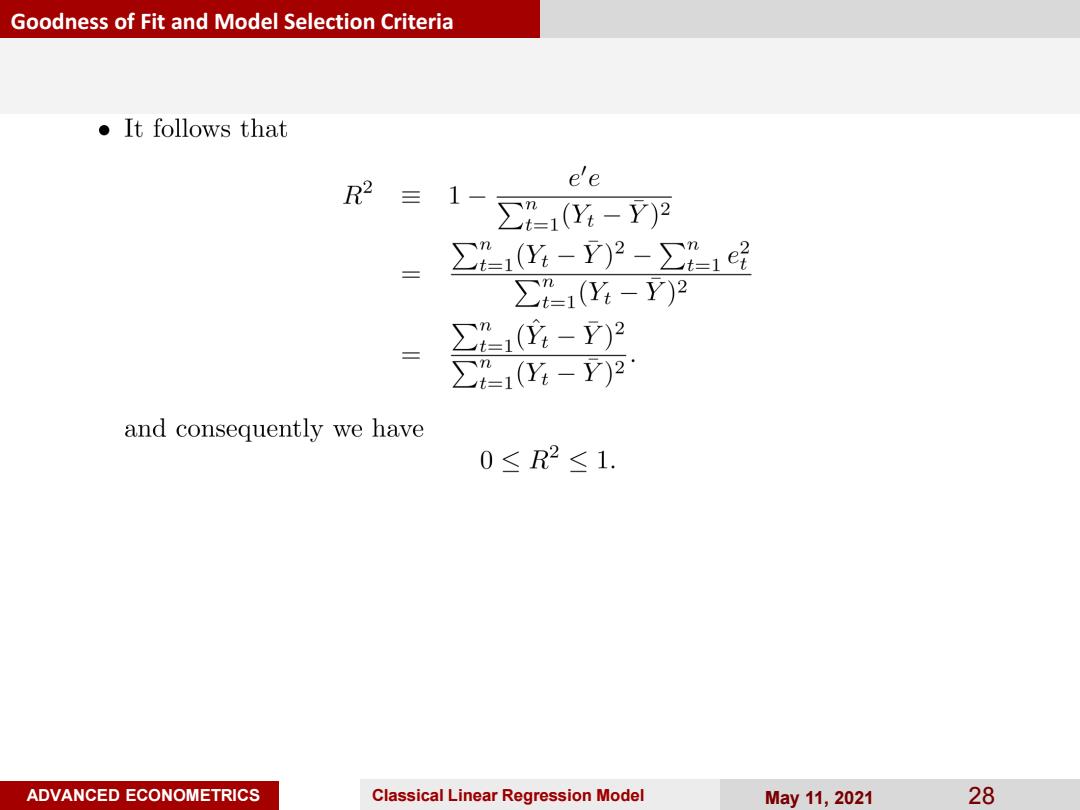
Goodness of Fit and Model Selection Criteria ●It follows that R2 e'e 三 ∑41(Y4-Y)2 三 ∑Y-Y)2-∑14 ∑-1(Y-Y)2 ∑1(应-Y)2 三 ∑1(Y-Y)2 and consequently we have 0≤R2≤1. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 28
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 28 Goodness of Fit and Model Selection Criteria

Goodness of Fit and Model Selection Criteria Questions: Can R2 be negative? .Yes,this is possible.If Xt does not contain the intercept,then the orthog- onal decomposition identity x-Y)2=∑Y-)2+∑ t=1 =1 t=1 generally no longer holds.As a consequence,R2 may be negative when there is no intercept!This is because the cross-product term 2∑应-)et t=1 may be negative. When Xt contains an intercept,the centered R2 has a similar interpreta- tion to the uncentered R2.That is,R2 measures the proportion of the sample variance of {Yi that can be explained by the linear predictor of Xt. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 29
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 29 Goodness of Fit and Model Selection Criteria Questions:

Goodness of Fit and Model Selection Criteria Example 2.[Capital Asset Pricing Model (CAPM)]: The classical CAPM is characterized by the equation Tit-rft=ai+Bi(rmt-rft)+Eit,t=1,...,n, where rit is the return on portfolio (or asset)i, -rft is the return on a risk-free asset, -rmt is the return on the market portfolio, rit-rft is the risk premium of portfolio i, -rmt-rft is the risk premium of the market portfolio,which is the only systematic market risk factor,and 一 eit is the idiosyncratic risk which can be eliminated by diversification if the eit are uncorrelated across different assets. In this model,R2 has an interesting economic interpretation:it is the proportion of the risk of portfolio i(as measured by the sample variance of its risk premium rit-rft)that is attributed to the market risk factor (rmt-rft).In contrast,1-R2 is the proportion of the risk of portfolio i that is contributed by the idiosyncratic risk factor eit. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 30
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 30 Goodness of Fit and Model Selection Criteria Example 2