
1、实验题目 激光散斑测量 2、实验目的 了解激光散斑的统计特性,学会两种处理激光散斑的重要方法:自相关函数法和互相关函数法。 3、实验器材: 激光散斑的基本概念:激光自散射体的表面漫反射或通过一个透明散射体(例如毛玻璃)时,在散 射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,称为激光散斑(Laser Speckles)或 斑纹。如果散射体足够粗糙,这种分布所形成的图样是非常特殊和美丽的(对比度为1)。 激光散斑是由无规散射体被相干光照射产生的,因此是一种随机过程。要研究它必须使用概率统计 的方法。通过统计方法的研究,可以得到对散斑的强度分布、对比度和散斑运动规律等特点的认 识。 米散哥的产生(图申为诱射,也可以是反射式的情形) 图1说明激光散斑具体的产生过程。当激光照射在粗表面上时,表面上的每一点都要散射光。因此 在空间各点都要接受到来自物体上各个点散射的光,这些光虽然是相干的,但它们的振幅和位相都 不相同,而且是无规分布的。来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加,形 成一定的统计分布。由于毛玻璃足够粗糖,所以激光散斑的亮暗对比强烈,而散斑的大小要根据光 路情况来决定。散斑场按光路分为两种,一种散斑场是在自由空间中传播而形成的(也称客观散 斑),另一种是由诱箱成像形成的(也称主观散斑)。在本实验中我们只研究前一种情况。当单色 激光穿过具有粗糙表面的玻璃板,在某一距离处的观察平面上可以看到大大小小的亮斑分布在几乎 全暗的背景上,当沿光路方向移动观察面时这些亮斑会发生大小的变化,如果设法改变激光照在玻 璃面上的面积,散斑的大小也会发生变化。由于这些散斑的大小是不一致的,因此这里所谓的大小 是指其统计平均值。它的变化规律可以用相关函数来描述。 ■激光散斑光强分布的相关函数的概念: ●自相关函数 假设观察面任意两点上的散斑光强分布为I(x1,y1),I(x2,y2),我们定义光强分布的自相关函数 为
1、实验题目 激光散斑测量 2、实验目的 了解激光散斑的统计特性,学会两种处理激光散斑的重要方法:自相关函数法和互相关函数法。 3、实验器材: 氦氖激光器,可调衰减器,扩束器,透镜,毛玻璃,CCD,计算机。 4、实验原理 激光散斑的基本概念:激光自散射体的表面漫反射或通过一个透明散射体(例如毛玻璃)时,在散 射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,称为激光散斑(Laser Speckles)或 斑纹。如果散射体足够粗糙,这种分布所形成的图样是非常特殊和美丽的(对比度为1)。 激光散斑是由无规散射体被相干光照射产生的,因此是一种随机过程。要研究它必须使用概率统计 的方法。通过统计方法的研究,可以得到对散斑的强度分布、对比度和散斑运动规律等特点的认 识。 图1 光散斑的产生(图中为透射式,也可以是反射式的情形) 图1说明激光散斑具体的产生过程。当激光照射在粗糙表面上时,表面上的每一点都要散射光。因此 在空间各点都要接受到来自物体上各个点散射的光,这些光虽然是相干的,但它们的振幅和位相都 不相同,而且是无规分布的。来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加,形 成一定的统计分布。由于毛玻璃足够粗糙,所以激光散斑的亮暗对比强烈,而散斑的大小要根据光 路情况来决定。散斑场按光路分为两种,一种散斑场是在自由空间中传播而形成的(也称客观散 斑),另一种是由透镜成像形成的(也称主观散斑)。在本实验中我们只研究前一种情况。当单色 激光穿过具有粗糙表面的玻璃板,在某一距离处的观察平面上可以看到大大小小的亮斑分布在几乎 全暗的背景上,当沿光路方向移动观察面时这些亮斑会发生大小的变化,如果设法改变激光照在玻 璃面上的面积,散斑的大小也会发生变化。由于这些散斑的大小是不一致的,因此这里所谓的大小 是指其统计平均值。它的变化规律可以用相关函数来描述。 n激光散斑光强分布的相关函数的概念: l自相关函数 假设观察面任意两点上的散斑光强分布为I(x1,y1),I(x2,y2),我们定义光强分布的自相关函数 为:

Gx,片:x2,y2)=<1(x1)1(x22)> 其中I(X1Y1)表示观察面上任一点Q1的光强,I(x2,y2)表示观察面上另一点Q2上的光强,()表 示求统计平均值。根据光学知识我们知道: 1(x,)=U(x,y)U'(x,y) (2 式中U(X,y)表示光场的复振幅。当玻璃板表面足够粗糙(毛玻璃)时,根据散斑统计学的理论我们可 以得到如下的公式: G(,为:xy)=<1(x,y)1(x2,)>+kU(x1y)U^(x2,y)> =<1>21+4(名,:x2] (3) 式中u(x1y1:x2,y2)=(U(x1,y1)U*(x2,y2))2/(I)2称做复相干系数。由于激光器 出射的光斑为高斯分布的(参见1),根据衍射理论可推出其复相干系数(推导方法用菲涅尔衍射 公式,参见62)为: 4x1为;,y2)=-(6x2+4y2)1S2] (④ 式中△x=(x2x1),Ay=(y2-y1),(3)式化为: G△x,y)=<1>2(1+ep[-(△x2+4y21S2]) () 进行归一化处理,可以得到归一化的自相关函数为: gx,4)=G△x)1<1>2=1+ep[-(x2+△y2)1S2](0 其中S的意义即代表散斑的平均半径。从62中可以知道S与激光高斯光斑半径W(在毛玻璃上的光 斑)的关系式为 S=21极 因此测量出S的大小就可以求出W ●两个散斑场光强分布的互相关函数 假设观察面任意一点Q1上的散斑光强分布为【(X1y1),当散射体发生一个变化后(如散射体发生 个微小的平移。=,+d,)观察面任意一点Q2上的散斑光强分布为1X2,y2)我们定义光强分 布的互相关函数为: C(6,4:x3)=<1(x1,)1'(x,%)> 司上面一样有: 1(x,)=U(x,y)U'(x,) (9) 1'(x,=U(x,)U(x,y》 (10) 式中U(x,y)和U`(x,y)分别表示两个散斑光场的复振幅。还是根据散斑统计学的理论我们可以得到 如下的公式: Ce(1为:x2)=<1'(61,)(xy)>+kU(6)U(x2,2)> =<1>2[1+4c(%1,为:x2,y2】 (1) 式中C(x1y1:2y2)=《U(x1,y1)U*(x2,y22〈I)2称作复互相干系数。根据衍射理 论可推出其复相干系数(推导方法用菲涅尔衍射公式,参见63)为:
其中I(x1,y1)表示观察面上任一点Q1的光强,I(x2,y2)表示观察面上另一点Q2上的光强,〈〉表 示求统计平均值。根据光学知识我们知道: 式中U(x,y)表示光场的复振幅。当玻璃板表面足够粗糙(毛玻璃)时,根据散斑统计学的理论我们可 以得到如下的公式: 式中m(x 1,y1;x2, y 2)=|〈U(x 1, y 1) U*(x 2, y 2) 〉|2¤〈I〉2称做复相干系数。由于激光器 出射的光斑为高斯分布的(参见6.1),根据衍射理论可推出其复相干系数(推导方法用菲涅尔衍射 公式,参见6.2)为: 式中Dx=(x2-x1),Dy=(y2-y1),(3)式化为: 进行归一化处理,可以得到归一化的自相关函数为: 其中S的意义即代表散斑的平均半径。从6.2中可以知道S与激光高斯光斑半径W(在毛玻璃上的光 斑)的关系式为 因此测量出S的大小就可以求出W。 l两个散斑场光强分布的互相关函数 假设观察面任意一点Q1上的散斑光强分布为I(x1,y1),当散射体发生一个变化后(如散射体发生一 个微小的平移 )观察面任意一点Q2上的散斑光强分布为I’(x2,y2) 我们定义光强分 布的互相关函数为: 同上面一样有: 式中U(x,y)和U‘(x,y)分别表示两个散斑光场的复振幅。还是根据散斑统计学的理论我们可以得到 如下的公式: 式中mC(x1,y1;x2,y 2)=|〈U‘(x 1, y 1)U*(x 2, y 2)|2¤〈I〉2称作复互相干系数。根据衍射理 论可推出其复相干系数(推导方法用菲涅尔衍射公式,参见6.3)为:
Hc()=exp(- a++B1pp-y++B风 2 2 (12 式中x=(x2x1,4y=(y2y1) 所以,两个散斑场的互相关函数为: Ce(x)=<1>21+ep6 4+3py* 1) 进行归一化处理,可以得到归 化的互相关函数为: (14) 5、实验内容 5.1激光散斑照相实验 1.1、根据激光散斑照相实验装配图安装所有的器件,将导轨用M6螺钉固定在光学平台上。 普光断斑照相验 注意:在安装CMOS相机时,请根据螺纹螺距区分英制与公制螺纹孔,如需要使用英制1/4”-20螺纹 孔连接CMOS时,请使用英制-公制螺纹转接头,如下图: 英制公制螺纹转接头 1.2、将所有器件调整至同心等高, 1.3、打开并调整激光器,使发射的激光水平,在光路中放入空间滤波器,在调整空间滤波器之前, 先去掉针孔,当物镜出射的光斑中心沿水平方向时,调节完毕。放入针孔,推动物镜旋钮靠近小 孔,推动过程中,不断调整小孔位置使得透射光斑最亮,光通过滤波器后检查射出的光点是最亮 的,无衍射条纹,光斑变得均匀时,说明已经调好。 1.4、使用平凸透镜将激光光束准直,观察光斑远近大小尺寸,调节平凸透镜与空间滤波器的距离。 当光斑在远近处直径一致时,认为光束准直完成
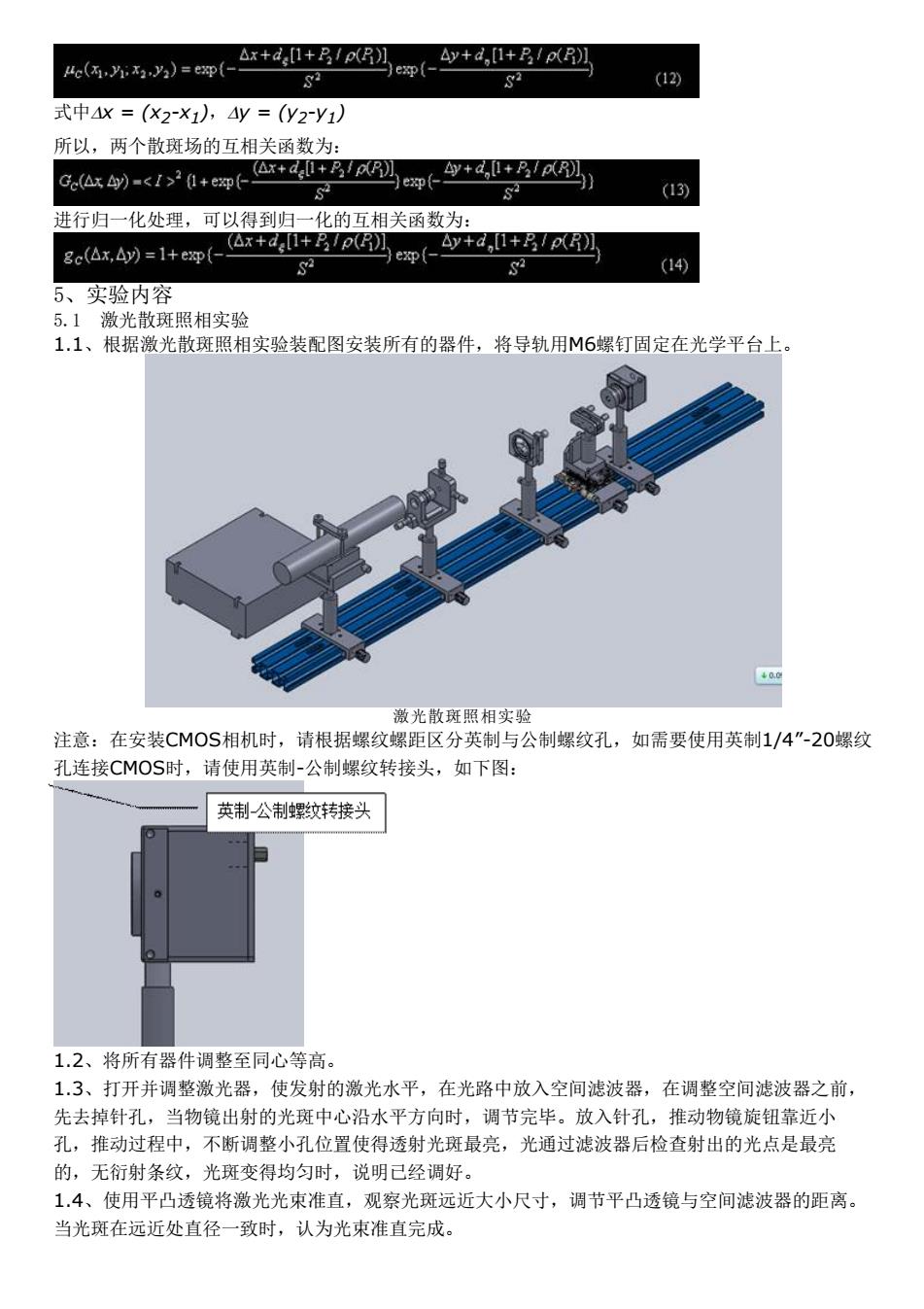
式中Dx = (x2-x1),Dy = (y2-y1) 所以,两个散斑场的互相关函数为: 进行归一化处理,可以得到归一化的互相关函数为: 5、实验内容 5.1 激光散斑照相实验 1.1、根据激光散斑照相实验装配图安装所有的器件,将导轨用M6螺钉固定在光学平台上。 激光散斑照相实验 注意:在安装CMOS相机时,请根据螺纹螺距区分英制与公制螺纹孔,如需要使用英制1/4”-20螺纹 孔连接CMOS时,请使用英制-公制螺纹转接头,如下图: 1.2、将所有器件调整至同心等高。 1.3、打开并调整激光器,使发射的激光水平,在光路中放入空间滤波器,在调整空间滤波器之前, 先去掉针孔,当物镜出射的光斑中心沿水平方向时,调节完毕。放入针孔,推动物镜旋钮靠近小 孔,推动过程中,不断调整小孔位置使得透射光斑最亮,光通过滤波器后检查射出的光点是最亮 的,无衍射条纹,光斑变得均匀时,说明已经调好。 1.4、使用平凸透镜将激光光束准直,观察光斑远近大小尺寸,调节平凸透镜与空间滤波器的距离。 当光斑在远近处直径一致时,认为光束准直完成

1.5、调节毛玻璃的位置与高低,使光斑照射在完全毛玻璃上。 1.6、打开相机的采集程序,使用连续采集模式。调节相机的位置与高低,使光照射在相机的适当位 置上。此时如果显示图像亮度过高适当减小相机的增益值和快门速度。(注:尽量缩进相机与毛玻 璃的距离) 1.7、采集并保存此时相机上的图像。 1.8、转动精密平移台上的千分尺,使毛玻璃向左右移动一定位置,(例 如0.5mm、1mm,-0.5mm、 -1mm),采集并保存此时相机上的图像 1.9、更换不同的位移量,重复上步骤3次,点击打开软件“LESPI”。 激光散斑实 南可 1.10、点击“原始散斑图”,按照路径选择原始图片,点击“平移散斑图”,按照路径选择位移后 图片 1.11、点击“互相关计算”进行计算,测出其偏移量
1.5、调节毛玻璃的位置与高低,使光斑照射在完全毛玻璃上。 1.6、打开相机的采集程序,使用连续采集模式。调节相机的位置与高低,使光照射在相机的适当位 置上。此时如果显示图像亮度过高适当减小相机的增益值和快门速度。(注:尽量缩进相机与毛玻 璃的距离) 1.7、采集并保存此时相机上的图像。 1.8、转动精密平移台上的千分尺,使毛玻璃向左右移动一定位置,(例 如 0.5mm、 1mm, -0.5mm、 -1mm),采集并保存此时相机上的图像。 1.9、更换不同的位移量,重复上步骤3次,点击打开软件“LESPI”。 1.10、点击“原始散斑图”,按照路径选择原始图片,点击“平移散斑图”,按照路径选择位移后 图片。 1.11、点击“互相关计算”进行计算,测出其偏移量

藏光散斑哈 1.12、,然后点击“散斑半径计算”,计算得出散斑半径。 藏光散斑实 1.13、转动侧升降台上的千分尺,重复步骤8~12,比较毛玻璃竖直移动位移和软件输出结果之间 的差距。 5.2激光散斑照相实验 2.1、根据激光散斑照相实验装配图安装所有的器件。 激光散斑照相实验
1.12、,然后点击“散斑半径计算”,计算得出散斑半径。 1.13、转动侧升降台上的千分尺,重复步骤8~12,比较毛玻璃竖直移动位移和软件输出结果之间 的差距。 5.2 激光散斑照相实验 2.1、根据激光散斑照相实验装配图安装所有的器件。 激光散斑照相实验