
第三节机械循环热水供暖系统的水力计算方法和例题 计算方法及步骤: 1、在轴侧图上,进行管段编号,立管编号并注明各管段 的热负荷和长度,如图4-6所示: 2、确定最不利环路: 3、计算最不利环路各管段的管径: 4、确定立管IV的管径: 5、计算其他立管:方法同立管V: 6、结论:
LOGO 第三节 机械循环热水供暖系统的水力计算方法和例题 1、在轴侧图上,进行管段编号,立管编号并注明各管段 的热负荷和长度,如图4-6所示: 2、确定最不利环路: 计算方法及步骤: 3、计算最不利环路各管段的管径: 4、确定立管Ⅳ的管径: 5、计算其他立管: 6、结 论: 方法同立管Ⅳ:

第三节机械循环热水供暖系统的水力计算方法和例题 四、散热器进流系数的确定 1、进流系数概念 流入散热器流量与主管流量之比。 2、垂直单管顺流式热水供暖系统 (4)若散热器单侧连接时,a=1.0; (2)若散热器双侧连接,同时两侧散热器的支管管径及 其长度都相等时,a=0.5。当两侧散热器的支管管径或 长度不相等时,两侧散热器的进流系数就不相等;
LOGO 第三节 机械循环热水供暖系统的水力计算方法和例题 四、散热器进流系数的确定 ⑴ 若散热器单侧连接时,α=1.0; 1、进流系数概念 流入散热器流量与主管流量之比。 2、垂直单管顺流式热水供暖系统 ⑵ 若散热器双侧连接,同时两侧散热器的支管管径及 其长度都相等时,α=0.5。当两侧散热器的支管管径或 长度不相等时,两侧散热器的进流系数α就不相等;
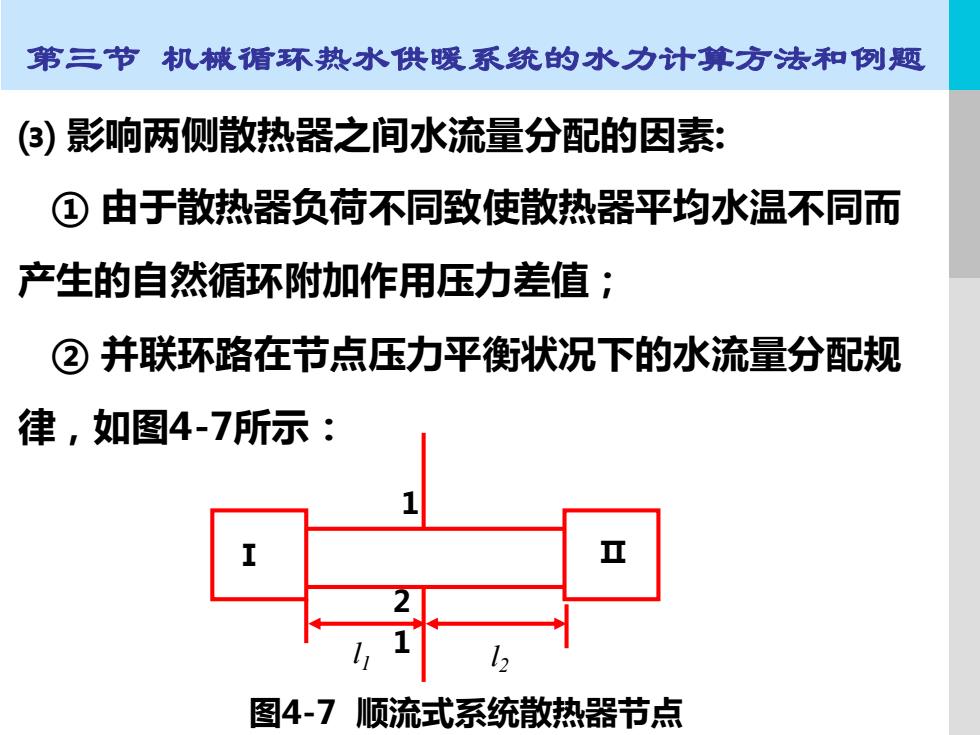
第三节机械循环热水供暖系统的水力计算方法和例题 (3)影响两侧散热器之间水流量分配的因素: ①由于散热器负荷不同致使散热器平均水温不同而 产生的自然循环附加作用压力差值: ②并联环路在节点压力平衡状况下的水流量分配规 律,如图4-7所示: 图4-7顺流式系统散热器节点
LOGO 第三节 机械循环热水供暖系统的水力计算方法和例题 ⑶ 影响两侧散热器之间水流量分配的因素: ② 并联环路在节点压力平衡状况下的水流量分配规 律,如图4-7所示: ① 由于散热器负荷不同致使散热器平均水温不同而 产生的自然循环附加作用压力差值; 1 1 2 Ⅰ Ⅱ l1 l2 图4-7 顺流式系统散热器节点

第三节机械循环热水供暖系统的水力计算方法和例题 (④)散热器进流系数的确定 ①在机械循环系统中,节点1、2并联环路的压力损 失较大,因此自然循环附加作用压力差值的影响,在一 般情况下可忽略不计,可以近似地按顺流式两侧的阻力 比,来确定散热器的进流系数; ②根据并联环路节点压力平衡原理,可列出下式: (R4+△Pi)I-2=(R42+△P2)hn-2 (4.22) 或根据当量长度法得: R(1,+1n)h-1-2=R(L2+l2h-n-2 (4.23)
LOGO 第三节 机械循环热水供暖系统的水力计算方法和例题 ⑷ 散热器进流系数的确定 ① 在机械循环系统中,节点1、2并联环路的压力损 失较大,因此自然循环附加作用压力差值的影响,在一 般情况下可忽略不计,可以近似地按顺流式两侧的阻力 比,来确定散热器的进流系数; ② 根据并联环路节点压力平衡原理,可列出下式: R1 l 1 Pj1 1 Ⅰ 2 R2 l 2 Pj2 1 Ⅱ 2 ( ) ( ) + − − = + − − (4.22) 或根据当量长度法得: R1 l 1 l d1 1 Ⅰ 2 R2 l 2 l d 2 1 Ⅱ 2 ) ( ) ( + − − = + − − (4.23)

第三节机械循环热水供暖系统的水力计算方法和例题 如支管41=d2,并假设两侧水的流动状况相同,摩擦 阻力系数入值近似相等,则上式可改为: G,21+l2=Gn24+l2h-n-2 (4.24) (4+lnh20+lh-2=G21G,2=(G,-G,21G (4.25) 将式(4.25)变换可得: a,=G,IG=(+a)ia N+ia)na (4.26) 若已知a及G值,流入散热器I和Ⅱ的水流量分别为: GI=QGL (4.27) Gn=(1-a)G (4.28)
LOGO 第三节 机械循环热水供暖系统的水力计算方法和例题 如支管d1=d2 ,并假设两侧水的流动状况相同,摩擦 阻力系数λ值近似相等,则上式可改为: GⅠ l l d Ⅰ GⅡ l 2 l d 2 1 Ⅱ 2 2 1 1 1 2 2 ) ( ) ( + − − = + − − (4.24) 2 2 1 2 2 1 1 1 2 2 2 1 2 (l + l d ) −Ⅰ− /(l + l d ) −Ⅱ− = GⅡ /GⅠ =(G −GⅠ)/GⅠ (4.25) 将式(4.25)变换可得: 1 1 1 1 1 1 2 2 2 1 2 / 1 ) /( ) − = Ⅰ = + + d −Ⅰ− + d −Ⅱ− G G ((l l l l (4.26) 若已知α及GL值,流入散热器Ⅰ和Ⅱ的水流量分别为: GⅠ =1 GL (4.27) GⅡ =(1−Ⅰ )GL (4.28)